A Esfera na Geometria Espacial
A Esfera é uma figura simétrica tridimensional que faz parte dos estudos de geometria espacial.
A esfera é um sólido geométrico de revolução formado pela rotação de um semicírculo em torno de seu eixo, que contém o diâmetro.
Ela é composta por uma superfície fechada e pelos pontos interiores, todos situados a uma distância igual ou menor que o raio em relação ao centro.
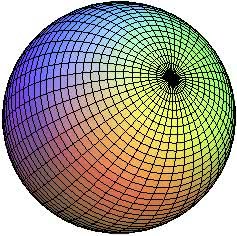
Elementos da Esfera
- Raio: segmento de reta que liga o centro a um ponto qualquer na superfície.
- Diâmetro: Segmento de reta que passa pelo centro, ligando dois pontos na superfície.
- Superfície Esférica: corresponde ao conjunto de pontos do espaço onde a distância do centro (O) é equivalente ao raio (R).
- Fuso Esférico: é a parte da superfície esférica que se obtém ao girar uma semicircunferência em um ângulo em torno do eixo que contém o diâmetro.

- Cunha Esférica: é um sólido, parte do volume da esfera obtido ao girar um semicírculo em torno do eixo que contém o diâmetro.

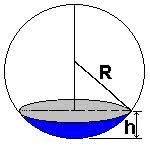
- Calota Esférica: corresponde a parte da esfera (semiesfera) cortada por um plano.
Fórmula da área da esfera
Para calcular a área da superfície esférica, utiliza-se a fórmula:
Onde:
- A é a área da esfera;
-
(Pi) é aproximadamente, 3,1415;
- r é o raio.
Exemplo de cálculo da área da esfera:
Calcule a área de uma bola de futebol que tem um raio de 11 centímetros.
Resolução:
Identificar os dados: Raio (r) = 11 cm.
Aplicar a fórmula:
Realizar os cálculos:
Resposta:
A área da superfície da bola de futebol é aproximadamente 1519,76 centímetros quadrados.
Você pode se interessar por aprender mais sobre área da superfície esférica.
Fórmula do volume da esfera
Para calcular o volume da esfera, utiliza-se a fórmula:
Onde:
- V é o volume da esfera;
-
(Pi) é aproximadamente, 3,1415;
- r é o raio.
Exemplo de cálculo do volume da esfera:
Calcule o volume da mesma bola de futebol que tem um raio de 11 centímetros.
Resolução:
Identificar os dados:Raio (r) = 11 cm.
Aplicar a fórmula:
Resposta:
O volume da bola de futebol é aproximadamente 5575,28 centímetros cúbicos.
Aprenda mais sobre volume da esfera.
Exercícios sobre a esfera
Exercício 1
Qual a área da esfera de raio √3 m?
Exercício 2
Qual o volume da esfera de raio 3 cm?
Para saber mais, leia também:
ASTH, Rafael. A Esfera na Geometria Espacial. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/a-esfera-na-geometria-espacial/. Acesso em:


