Operações com números decimais

Revisão por Rafael C. Asth

Professor de Matemática e Física

Os números decimais são aqueles que pertencem ao conjunto dos números racionais (Q) e são escritos com a utilização de uma vírgula. Esses números são formados por uma parte inteira e uma parte decimal, que se apresenta à direita da vírgula.

Exemplo de um número decimal:

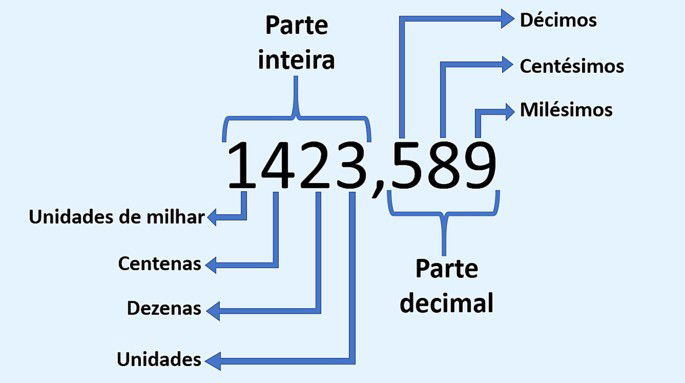
As operações matemáticas básicas – adição, subtração, multiplicação e divisão – são realizadas com os números decimais mediante a aplicação de algumas regras que veremos a seguir.

Multiplicação de números decimais

A operação de multiplicação com números decimais pode ser feita efetuando uma multiplicação normalmente e ao resultado adiciona-se uma vírgula para que o número de casas decimais seja igual à soma das casas decimais dos números multiplicados.

Outra maneira é escrever os números decimais na forma de fração e multiplicar numerador com numerador e denominador com denominador.

Exemplo 1: Multiplicação de um número decimal por um número natural

Ao multiplicar um número decimal por um número natural devemos repetir no resultado o número de casas decimais.

3,25 x 4

$tabela linha com célula com 3 com negrito 1 sobrescrito fim da célula vírgula célula com 2 com negrito 2 sobrescrito fim da célula 5 linha com reto x blank blank 4 fim da tabela espaço 13 espaço vírgula espaço 0 espaço espaço 0 espaço espaço espaço em moldura superior fecha moldura$

Isso seria o mesmo que:

$reto I. espaço 4 espaço reto x espaço 3 vírgula 25 espaço igual a espaço 3 vírgula 25 espaço mais espaço 3 vírgula 25 espaço mais espaço 3 vírgula 25 espaço mais espaço 3 vírgula 25 espaço igual a espaço 13 II. espaço 4 espaço reto x espaço 3 vírgula 25 com parêntese inferior abaixo espaço igual a espaço 4 espaço reto x espaço 325 sobre 100 igual a espaço numerador 13 horizontal risco 00 sobre denominador 1 horizontal risco 00 fim da fração espaço igual a espaço 13$

Exemplo 2: Multiplicação entre números decimais

Para multiplicar números decimais realizamos, primeiramente, a multiplicação normalmente, sem levar em consideração a vírgula.

Após isso, no resultado deve ser acrescentado a vírgula com o número de casas decimais após ela que corresponde à soma das casas decimais dos números multiplicados.

Método 1:

$espaço espaço espaço 3 vírgula 5 espaço seta para a esquerda um espaço algarismo espaço após espaço reto a espaço vírgula reto x espaço 2 vírgula 5 espaço espaço seta para a esquerda um espaço algarismo espaço após espaço reto a espaço vírgula espaço espaço espaço 175 espaço espaço em moldura superior fecha moldura espaço espaço espaço 70 mais espaço espaço 8 negrito vírgula 75 espaço espaço em moldura superior fecha moldura seta para a esquerda dois espaço algarismos espaço após espaço reto a espaço vírgula$

Método 2:

$3 vírgula 5 com parêntese inferior abaixo espaço reto x espaço 2 vírgula 5 com parêntese inferior abaixo espaço igual a espaço 35 sobre 10 reto x 25 sobre 10 igual a numerador 35 espaço reto x espaço 25 sobre denominador 10 espaço reto x espaço 10 fim da fração igual a 875 sobre 100 igual a 8 vírgula 75$

Exemplo 3: Multiplicação de um número decimal por 10, 100, 1000, …

Quando multiplicamos um número decimal por 10, 100, 1000, … devemos “andar” com a vírgula para direita de acordo com o número de zeros.

Exemplo:

$5 vírgula 4321 espaço reto x espaço 1 negrito 0 espaço igual a espaço 54 negrito vírgula 321 5 vírgula 4321 espaço reto x espaço 1 negrito 00 espaço igual a espaço 543 negrito vírgula 21 5 vírgula 4321 espaço reto x espaço 1 negrito 000 espaço igual a espaço 5432 negrito vírgula 1$

Portanto, ao multiplicar por:

10, “andamos” com a vírgula uma casa para direita;
100, “andamos” com a vírgula duas casas para direita;
1000, “andamos” com a vírgula três casas para direita e assim sucessivamente.

Adição de números decimais

Na soma de números decimais devemos somar os respectivos números de cada casa decimal, ou seja, décimos são somados com décimos, centésimos com centésimos e milésimos com milésimos.

Para facilitar os cálculos, escreva os números de forma que as vírgulas fiquem uma abaixo da outra e no resultado a vírgula também deve estar alinhada.

Exemplo 1: 0,6 + 1,2

$tabela linha com blank blank blank blank linha com blank célula com espaço espaço espaço espaço espaço espaço espaço 0 vírgula 6 fim da célula blank blank linha com blank célula com espaço espaço espaço espaço mais espaço 1 vírgula 2 espaço espaço em moldura inferior fecha moldura fim da célula blank blank linha com blank célula com espaço espaço espaço espaço espaço espaço espaço 1 vírgula 8 fim da célula blank blank fim da tabela$

Portanto, 0,6 + 1,2 = 1,8.

Se um número apresentar mais casas decimais que o outro, você pode adicionar zeros ao número com menos casas após a vírgula para igualar a quantidade de termos.

Exemplo 2: 2,582 + 5,6 + 7,31

$tabela linha com célula com espaço espaço espaço reto U fim da célula blank reto d reto c reto m blank linha com célula com espaço espaço espaço espaço 2 com negrito 1 sobrescrito fim da célula vírgula 5 8 2 blank linha com célula com espaço espaço espaço espaço 5 fim da célula vírgula 6 negrito 0 negrito 0 blank linha com célula com mais espaço 7 fim da célula vírgula 3 1 negrito 0 blank fim da tabela espaço espaço espaço espaço 15 espaço vírgula espaço espaço espaço 4 espaço espaço 9 espaço espaço espaço 2 espaço espaço espaço espaço em moldura superior fecha moldura$

Portanto, 2,582 + 5,6 + 7,31 = 15,492.

Subtração de números decimais

Assim como na adição, a subtração de números decimais deve ser feita alinhando-se as vírgulas.

Exemplo 1: 3,57 – 1,45

$tabela linha com célula com espaço espaço espaço espaço reto U fim da célula blank reto d reto c linha com célula com espaço espaço espaço espaço 3 fim da célula vírgula 5 7 linha com célula com menos espaço 1 fim da célula vírgula 4 5 fim da tabela espaço espaço espaço espaço espaço espaço 2 espaço espaço vírgula espaço espaço 1 espaço espaço 2 espaço espaço espaço espaço em moldura superior fecha moldura$

Portanto, 3,57 – 1,45 = 2,12.

Exemplo 2: 15,879 – 12,564

$tabela linha com célula com espaço espaço espaço reto D fim da célula reto U blank reto d reto c linha com célula com espaço espaço espaço espaço 1 fim da célula 5 vírgula célula com 8 fim da célula 7 linha com célula com menos espaço 1 fim da célula 2 vírgula 5 6 fim da tabela tabela linha com reto m linha com célula com 9 fim da célula linha com 4 fim da tabela espaço espaço espaço espaço espaço espaço 0 espaço espaço 3 espaço espaço vírgula espaço espaço espaço 3 espaço espaço 1 espaço espaço 5 espaço espaço espaço espaço em moldura superior fecha moldura$

Portanto, 15,879 – 12,564 = 3,315.

Divisão de números decimais

Para efetuar a divisão, tanto o dividendo quanto o divisor devem ter o mesmo número de casas decimais.

Exemplo 1: Divisão de um número decimal por outro número decimal

Se, por exemplo, os dois termos da divisão possuem um algarismo à direita da vírgula, então podemos multiplicar por 10 e eliminá-la. A seguir, efetuamos a divisão normalmente.

1º passo:

$tabela linha com célula com 3 vírgula 5 com parêntese inferior abaixo espaço dividido por espaço 0 vírgula 5 com parêntese inferior abaixo fim da célula célula com seta para a direita com reto x espaço 10 espaço sobrescrito fim da célula 35 célula com dividido por espaço 5 espaço fim da célula linha com blank blank blank blank linha com blank blank blank blank fim da tabela$

2º passo:

$tabela linha com célula com espaço espaço espaço espaço espaço espaço 35 fim da célula célula com espaço espaço espaço 5 espaço espaço espaço em moldura inferior fecha moldura em moldura esquerda fecha moldura fim da célula linha com célula com espaço menos espaço 35em moldura inferior fecha moldura fim da célula 7 linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço 0 fim da célula blank fim da tabela$

Portanto, 3,5 $dividido por$ 0,5 = 7

Exemplo 2: Divisão de um número decimal por um número natural

Para efetuar esse tipo de divisão devemos reescrever o divisor para que apresente o mesmo número de casas decimais que o dividendo. Após isso, eliminamos a vírgula, multiplicando os dois termos por 10, 100, 1000… conforme o número de casas decimais, e realizamos a divisão.

1º passo:

20,5 $dividido por$ 5 → 20,5 $dividido por$ 5,0

2º passo:

$tabela linha com célula com 20 vírgula 5 com parêntese inferior abaixo espaço dividido por espaço 5 vírgula 0 com parêntese inferior abaixo fim da célula célula com seta para a direita com reto x espaço 10 espaço sobrescrito fim da célula 205 célula com dividido por espaço 50 fim da célula fim da tabela$

3º passo:

Observe que ocorreu uma divisão não exata, ou seja, a operação apresenta resto. Para continuar, devemos adicionar uma vírgula ao divisor e um zero ao resto.

4º passo:

$tabela linha com célula com espaço espaço espaço espaço 205 fim da célula célula com espaço espaço espaço 50 espaço espaço espaço em moldura inferior fecha moldura em moldura esquerda fecha moldura fim da célula linha com célula com menos espaço 200em moldura inferior fecha moldura fim da célula célula com 4 negrito vírgula 1 fim da célula linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço 5 negrito 0 fim da célula blank linha com célula com espaço espaço espaço espaço espaço menos espaço 50em moldura inferior fecha moldura espaço fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 0 fim da célula blank fim da tabela$

Portanto, 20,5 $dividido por$ 5 = 4,1.

Exemplo 3: Divisão de um número natural por um número decimal

Para efetuar a divisão devemos adicionar uma vírgula ao dividendo e, em seguida, colocamos algarismos zeros à direita da vírgula igual ao número de casas decimais do divisor.

Se, por exemplo, o divisor apresenta uma casa decimal, então adicionamos uma vírgula seguida de um algarismo 0 ao dividendo. Multiplicando os dois termos por 10, eliminamos a vírgula e realizamos a operação normalmente.

1º passo:

14 $dividido por$ 0,7 → 14,0 $dividido por$ 0,7

2º passo:

$tabela linha com célula com 14 vírgula 0 com parêntese inferior abaixo espaço dividido por espaço 0 vírgula 7 fim da célula célula com seta para a direita com reto x espaço 10 espaço sobrescrito fim da célula 140 célula com dividido por espaço 7 fim da célula fim da tabela$

3º passo:

$tabela linha com célula com espaço espaço espaço espaço espaço espaço 14 apóstrofo 0 fim da célula célula com espaço espaço 7 espaço espaço espaço em moldura inferior fecha moldura em moldura esquerda fecha moldura fim da célula linha com célula com menos espaço 14em moldura inferior fecha moldura fim da célula 20 linha com célula com espaço espaço espaço espaço espaço espaço espaço 00 fim da célula blank linha com célula com espaço espaço espaço espaço menos espaço 00em moldura inferior fecha moldura fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço 0 fim da célula blank fim da tabela$

Portanto, 14 $dividido por$ 0,7 = 20.

Saiba mais sobre a divisão com números decimais.

Exercícios sobre operações com números decimais

Questão 1

Realize as operações com os números decimais a seguir.

a) 0,22 + 0,311
b) 1,58 – 0,4
c) 2,44 $dividido por$ 0,5
d) 5,35 x 1,3

Ver Resposta

Respostas corretas:

a) 0,22 + 0,311 = = 0,531
b) 1,58 – 0,4 = 1,18
c) 2,44 $dividido por$ 0,5 = 4,88
d) 5,35 x 1,3 = 6,955

a) 0,22 + 0,311 = 0,531

$tabela linha com célula com espaço espaço espaço reto U fim da célula blank reto d reto c reto m blank linha com célula com espaço espaço espaço espaço 0 fim da célula vírgula 2 2 negrito 0 blank linha com célula com mais espaço 0 fim da célula vírgula 3 1 1 blank fim da tabela espaço espaço espaço espaço espaço 0 espaço espaço vírgula espaço espaço espaço 5 espaço espaço 3 espaço espaço 1 espaço espaço espaço espaço em moldura superior fecha moldura$

b) 1,58 – 0,4 = 1,18

$tabela linha com célula com espaço espaço espaço reto U fim da célula blank reto d reto c linha com célula com espaço espaço espaço espaço 1 fim da célula vírgula 5 8 linha com célula com menos espaço 0 fim da célula vírgula 4 negrito 0 fim da tabela espaço espaço espaço espaço espaço 1 espaço espaço vírgula espaço espaço espaço 1 espaço espaço 8 espaço espaço espaço espaço espaço em moldura superior fecha moldura$

c) 2,44 : 0,5 = 4,88

2,44 : 0,5 → 2,44 : 0,50

$tabela linha com célula com 2 vírgula 44 com parêntese inferior abaixo espaço dividido por espaço 0 vírgula 50 com parêntese inferior abaixo fim da célula célula com seta para a direita com reto x espaço 100 espaço sobrescrito fim da célula 244 célula com dividido por espaço 50 fim da célula fim da tabela$

$tabela linha com célula com espaço espaço espaço espaço espaço espaço 244 fim da célula célula com espaço espaço 50 espaço espaço espaço em moldura inferior fecha moldura em moldura esquerda fecha moldura fim da célula linha com célula com espaço espaço menos espaço 200em moldura inferior fecha moldura fim da célula célula com 4 negrito vírgula 88 fim da célula linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 44 negrito 0 fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço menos 400em moldura inferior fecha moldura fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 40 negrito 0 fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço menos 400em moldura inferior fecha moldura fim da célula blank linha com célula com espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 0 fim da célula blank fim da tabela$

d) 5,35 x 1,3 = 6,955

$espaço espaço 5 com negrito 1 sobrescrito vírgula 3 com negrito 1 sobrescrito 5 espaço seta para a esquerda dois espaço algarismos espaço após espaço reto a espaço vírgula reto x espaço espaço 1 vírgula 3 espaço espaço seta para a esquerda um espaço algarismo espaço após espaço reto a espaço vírgula espaço espaço 1605 espaço espaço em moldura superior fecha moldura espaço espaço 535 mais espaço 6 negrito vírgula 9 55 espaço espaço em moldura superior fecha moldura seta para a esquerda três espaço algarismos espaço após espaço reto a espaço vírgula$

Questão 2

João emprestou ao seu irmão R$ 30,00. Após alguns dias ele recebeu R$ 22,50 de volta, mas seu irmão precisou novamente de sua ajuda e ele lhe entregou outros R$ 15,00. Mais tarde, o irmão de João lhe devolveu R$ 19,50. Quanto o irmão ainda lhe deve?

a) R$ 2,00.
b) R$ 5,50.
c) R$ 4,50.
d) R$ 3,00.

Ver Resposta

Alternativa correta: d) R$ 3,00.

Primeiro empréstimo: R$ 30,00
Primeira devolução: R$ 22,50
Segundo empréstimo: R$ 15,00
Segunda devolução: R$ 19,50
Dívida: ?

1º passo: subtrair o valor que foi devolvido do primeiro empréstimo.

$espaço espaço espaço espaço espaço 30 vírgula 00 menos espaço 22 vírgula 50 espaço espaço espaço espaço espaço 07 vírgula 50 espaço espaço em moldura superior fecha moldura$

2º passo: somar o segundo empréstimo com o valor que o irmão ainda deve.

$espaço espaço espaço espaço espaço 15 vírgula 00 menos espaço espaço espaço 7 vírgula 50 espaço espaço espaço espaço espaço 22 vírgula 50 espaço espaço em moldura superior fecha moldura$

3º passo: subtrair a nova quantia devolvida.

$espaço espaço espaço espaço espaço 22 vírgula 50 menos espaço 19 vírgula 50 espaço espaço espaço espaço espaço 03 vírgula 00 espaço espaço em moldura superior fecha moldura$

Portanto, o irmão de João ainda lhe deve R$ 3,00.

Questão 3

Calcule:

a) O dobro de 0,58
b) Um terço de 9,6
c) 10 vezes 13 centésimos

Ver Resposta

Resposta correta:

a) O dobro de 0,58 é 1,16.

$espaço espaço 0 com negrito 1 sobrescrito vírgula 5 com negrito 1 sobrescrito 8 espaço seta para a esquerda d o i s espaço a l g a r i s m o s espaço a p ó s espaço a espaço v í r g u l a espaço espaço espaço reto x espaço espaço 2 espaço espaço 1 negrito vírgula 16 espaço espaço em moldura superior fecha moldura seta para a esquerda d o i s espaço a l g a r i s m o s espaço a p ó s espaço a espaço v í r g u l a$

b) Um terço de 9,6 é 3,2.

$9 vírgula 6 espaço reto x espaço 1 terço espaço igual a espaço numerador 9 vírgula 6 sobre denominador 3 fim da fração espaço igual a espaço 3 vírgula 2$

c) 10 vezes 13 centésimos é 1,3.

$13 sobre 100 igual a 0 vírgula 13$

$0 vírgula 13 espaço reto x espaço 10 espaço igual a espaço 1 vírgula 3$

Você também pode se interessar por:

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.