Adição

Rafael C. Asth

Professor de Matemática e Física

A adição é o ato de juntar elementos, uma das quatro operações básicas da aritmética. A adição está ligada a ideia de acrescentar. Toda vez que unimos novos elementos ou valores, estamos adicionando.

Em Matemática utiliza-se a símbolo + para representar uma adição.

Termos da adição

Cada elemento somado é chamado parcela. Uma adição pode ter pelo menos duas parcelas e até infinitas.

Exemplo
Ao juntar 300 gramas de arroz com 200 gramas de feijão, temos um prato com 500 gramas.

As parcelas são 300 e 200 e ao resultado, chamamos total ou soma. No exemplo, o resultado 500 é o total ou, a soma.

Conta de somar: cálculo da adição

Também conhecida como conta de mais ou, conta de somar, é um procedimento que nos ajuda a calcular. Este algoritmo da adição é muito útil, principalmente para adições com muitas parcelas ou valores grandes.

Ao efetuar uma adição, escrevem-se as parcelas umas sobre as outras, como uma “pilha” de parcelas e abaixo é feito um traço.

Realizamos a adição somando os algarismos com mesma ordem, começando pelas unidades. Após seguimos somando os algarismos, ordem por ordem.

Exemplo
23 + 15 = 38

Ao escrever os números, estes devem ser organizados colocando ordens iguais em uma mesma coluna. Unidades sobre unidades, dezenas sobre dezenas e assim por diante.

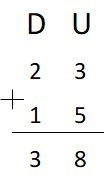
Adição com reserva ou reagrupamento

A Adição com reserva ou reagrupamento também é conhecida como: "vai um”, "vai dois" ... . Ao somar os algarismos em uma ordem, caso o resultado seja maior que 9, devemos acrescentar esta quantidade à ordem seguinte.

Lembre que não podemos escrever mais de um algarismo por ordem.

Exemplo
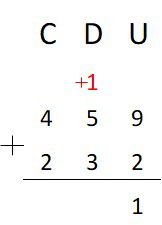
459 + 232 =

Na ordem das unidades temos 9 + 2 = 11. O número 11 pode ser escrito como 1 dezena + 1 unidade:

11 = 10 + 1

Esta dezena deve ser adicionada à coluna das dezenas.

Na coluna das dezenas temos +1 dezena que será acrescentada ao 5 e ao 3. Como 1 + 5 + 3 = 9, não é necessário acrescentar uma centena e assim, seguimos o cálculo.

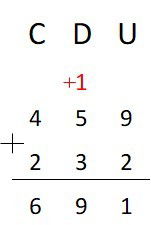
Este procedimento deve ser repetido em qualquer ordem caso a soma seja maior que 9. Ao completar uma ordem seguinte, devemos sempre acrescentá-la na coluna correta.

Propriedades da adição

A operação de adição com números naturais possui cinco propriedades e, no conjunto dos números inteiros há uma. Estas propriedades definem a adição e ajudam a calcular.

Propriedade Associativa

Podemos associar as parcelas de modo a facilitar o cálculo.

Exemplo
8 + 6 + 2 + 3= 19

Podemos associar as parcelas da seguinte forma:

8 + 2 + 6 + 3 = 19

10 + 9 = 19

Propriedade Comutativa

A ordem das parcelas não altera a soma.

12 + 3 = 15, assim como, 3 + 12 = 15.

Elemento neutro

O elemento neutro da adição é o zero, pois não altera o resultado.

Exemplos
5 + 0 = 5

4 + 0 + 5 = 9

0 + 37 = 37

Fechamento

A propriedade do fechamento define que ao somar dois ou mais números naturais, o resultado será sempre um número natural.

Exemplo

1 457 + 2 354 = 3 811

Lembre que o conjunto dos números naturais começa com o zero e vai ao infinito, avançando a cada uma unidade.

N = {0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}

Propriedade do elemento oposto ou simétrico

No conjunto dos números inteiros há a propriedade do elemento oposto ou simétrico, em que um número é oposto ou simétrico quando seu sinal é trocado. Ex.: O oposto ou simétrico de 2 é -2.

Ao somar números simétricos, o resultado é sempre zero.

Exemplos
3 + (-3) = 0

-17 + 17 = 0

256 + (-256) = 0

Veja também propriedades da adição.

Regra de sinais na adição (adição de números inteiros)

O conjunto dos números inteiros compreendem os números negativos e positivos. Também, o conjunto dos inteiros é infinito, tanto no sentido negativo quanto no positivo da reta.

Z = {...,-4, -3, -2, -1, 0, 1, 2, 3, 4, …}

Para somar números inteiros, respeitam-se algumas regras de sinais.

Sinais iguais
Se as parcelas possuem mesmo sinal, deve-se somar e repetir o sinal.

Exemplos
7 + 2 = 9

-14 - 3 = -17

Sinais diferentes
Se as parcelas possuem sinais diferentes, deve-se subtrair e manter o sinal do número com o maior valor absoluto.

- 21 + 12 = 21 - 12 = -9 (pois o sinal negativo está no 21)

15 - 17 = 17 - 15 = -2 (pois o sinal negativo está no 17)

Exercício de adição

Resolva as seguintes adições utilizando o algoritmo da adição.

a) 561 + 1364 =

b) 2641 + 3471 =

Veja subtração e divisão.

Curiosidade: os símbolos de + e -

Os símbolos de adição +, e subtração -, aparecem pela primeira vez na história em 1498, registrados no livro Aritmética Comercial, do alemão Johannes Widmann. Muito embora eram usados para representar excessos e déficits de mercadorias.

Em 1557 o inglês Robert Recorde em sua obra, Whetstone of Witte, empregou estes símbolos com o sentido usual de acrescentar e retirar.

Veja também: Plano de aula sobre adição para 1º ano com atividades

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.