Cálculo do Coeficiente Angular

Rosimar Gouveia

Professora de Matemática e Física

O coeficiente angular, também chamado de declividade de uma reta, determina a inclinação de uma reta.

Fórmulas

Para calcular o coeficiente angular de uma reta utiliza-se a seguinte fórmula:

m = tg α

Sendo m um número real e α o ângulo de inclinação da reta.

Atenção!

• Quando o ângulo é igual a 0º: m = tg 0 = 0
• Quando o ângulo α é agudo (menor que 90º): m = tg α > 0
• Quando o ângulo α é reto (90º): não é possível calcular o coeficiente angular, pois não existe a tangente de 90º
• Quando o ângulo α é obtuso (maior que 90º) : m = tg α < 0

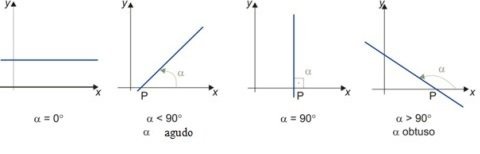
Representação das retas e seus ângulos

Para calcular o coeficiente angular de uma reta a partir de dois pontos devemos dividir a variação entre os eixos x e y:

Uma reta que passa por A (x_a,y_a) e B (x_b,y_b) temos a relação:

Essa relação pode ser escrita da seguinte forma:

Onde,

Δy: representa a diferença entre as ordenadas de A e B
Δx: representa a diferença entre as abcissas de A e B

Exemplo:

Para compreender melhor vamos calcular o coeficiente angular da reta que passa por A (– 5; 4) e B (3,2):

m = Δy/Δx
m = 4 – 2 / –5 – 3
m = 2/–8
m = –1/4

Esse valor é referente ao cálculo de diferença de A para B.

Da mesma forma, poderíamos calcular a diferença de B para A e o valor seria o mesmo:

m = Δy/Δx
m = 2 – 4 / –3 –(– 5)
m = –2/8
m = –1/4

Coeficiente Angular e Linear

Nos estudos das funções de primeiro grau calculamos os coeficiente angular e linear da reta.

Lembre-se que a função de primeiro grau é representada da seguinte maneira:

f(x) = ax + b

Onde a e b são números reais e a≠0.

Como vimos acima, o coeficiente angular é dado pelo valor da tangente do ângulo que a reta forma com o eixo de x.

Já o coeficiente linear é aquele que corta o eixo y do plano cartesiano. Na representação da função de primeiro grau f(x) = ax + b temos que:

a: coeficiente angular (eixo x)
b: coeficiente linear (eixo y)

Para saber mais, leia também:

• Equação da Reta
• Distância entre dois pontos
• Retas Paralelas
• Retas Perpendiculares

Exercícios de Vestibular com Gabarito

1. (UFSC-2011) A reta que passa pela origem e pelo ponto médio do segmento AB com A=(0,3) e B=(5,0) tem qual coeficiente angular?

a) 3/5
b) 2/5
c) 3/2
d) 1

2. (UDESC-2008) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:

a) 4
b) –5
c) 3
d) 2
e) 5

Leia também:

• Função Linear
• Função Afim
• Retas
• Exercícios sobre equação da reta resolvidos
• Ângulos

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.