Cônicas

As cônicas ou secções cônicas são curvas obtidas pela intersecção de um plano com um cone duplo. Conforme a inclinação desse plano, a curva será chamada de elipse, hipérbole ou parábola.

Quando o plano é paralelo à base do cone, a curva formada é uma circunferência, um caso particular da elipse. À medida que inclinamos o plano, surgem outras curvas, como ilustrado na imagem abaixo:

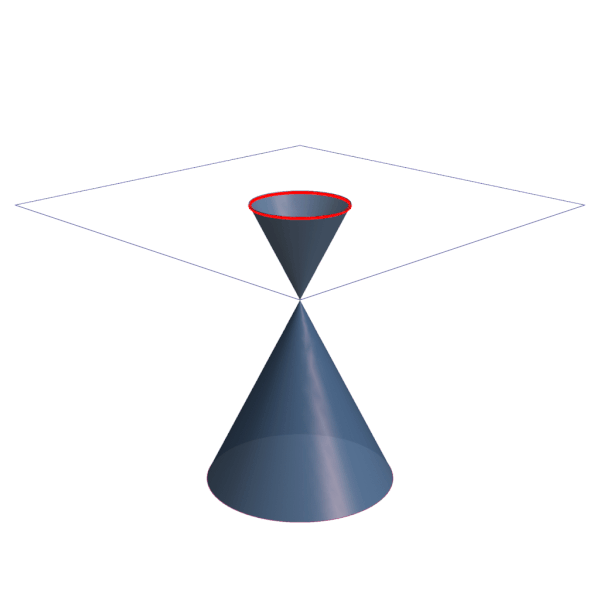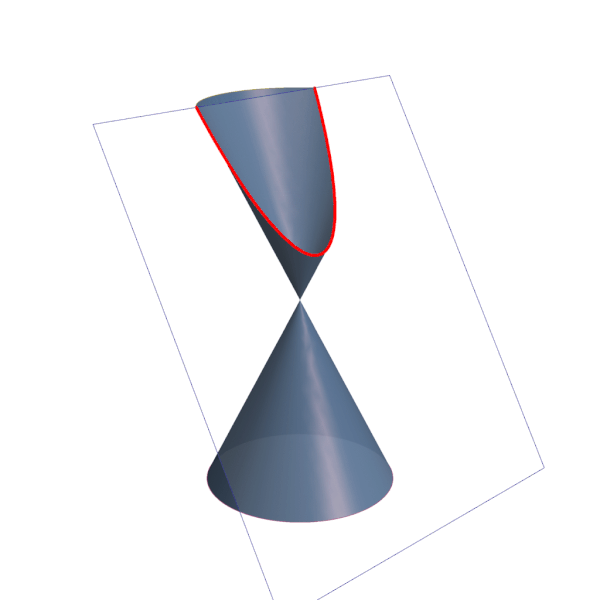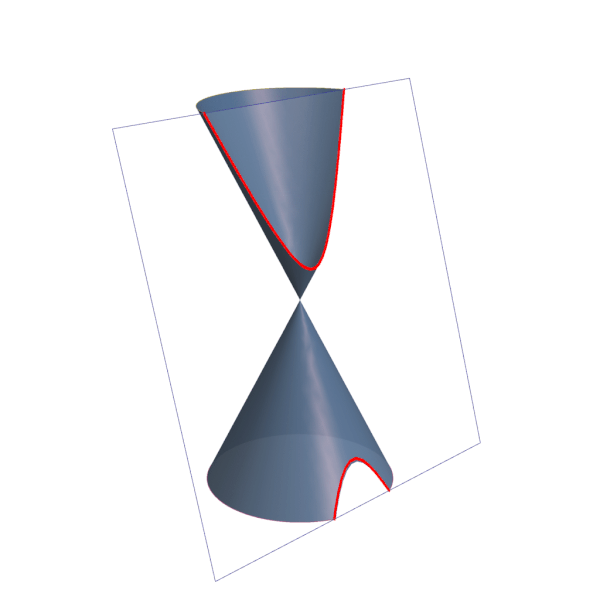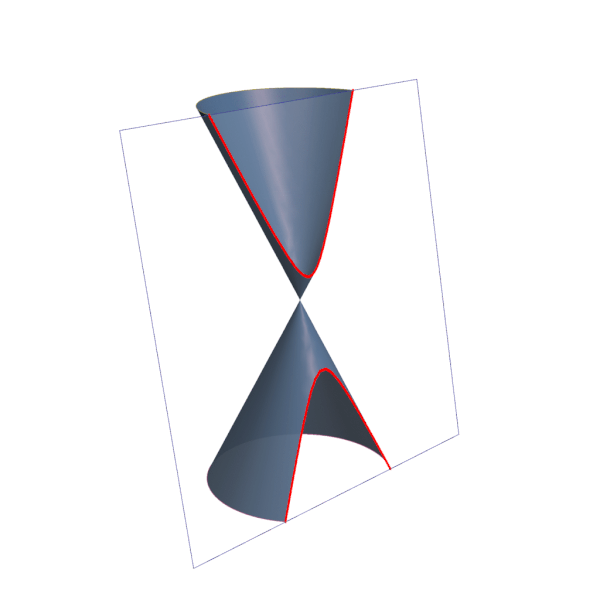
A intersecção de um plano com o vértice do cone pode ainda dar origem a um ponto, uma reta ou duas retas concorrentes. Neste caso, são chamadas de cônicas degeneradas.

O estudo das secções cônicas iniciou na Grécia antiga, onde foram identificadas diversas das propriedades geométricas. Entretanto, foi necessário alguns séculos para que a utilidade prática dessas curvas fosse identificada.

Elipse

A curva gerada quando um plano corta todas as geratrizes de um cone é chamada de elipse, neste caso, o plano não é paralelo à geratriz.

Desta forma, a elipse é o lugar geométrico dos pontos no plano cuja soma das distâncias (d₁ + d₂) a dois pontos fixos do plano, chamados de foco (F₁ e F₂), é um valor constante.

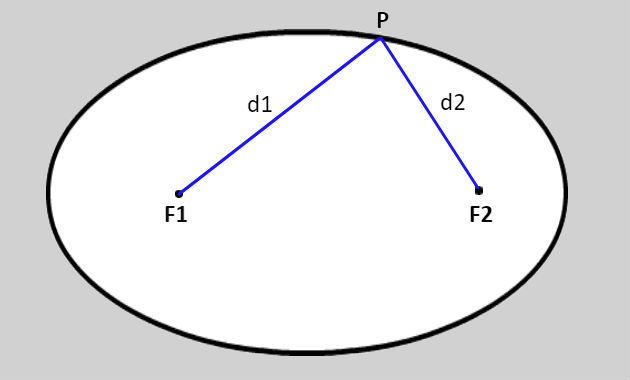
A soma das distâncias d₁ e d₂ é indicada por 2a, ou seja, 2a = d₁ + d₂ e a distância entre os focos é chamada de 2c, sendo que 2a > 2c.

A maior distância entre dois pontos pertencentes à elipse é chamada de eixo maior e seu valor é igual à 2a. Já a menor distância é chamada de eixo menor sendo indicada por 2b.

O número é chamado de excentricidade e indica o quanto a elipse é "achatada".

Temos ainda a seguinte relação:

a² = b² + c²

Sendo:

• a: medida do semieixo maior;
• b: medida do semieixo menor;
• c: metade da distância focal.

Equação reduzida da elipse

Podemos representar uma elipse usando um plano cartesiano, conforme figura abaixo:

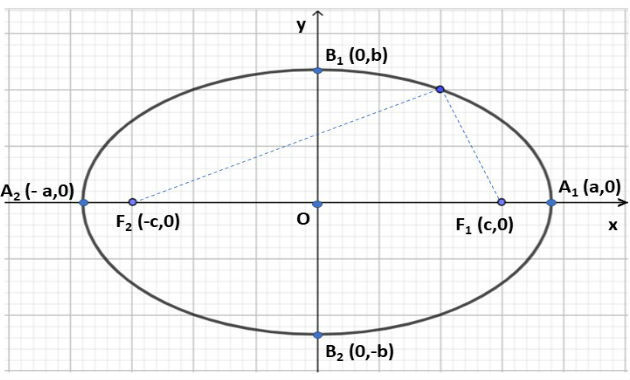
Neste caso, a elipse possui centro na origem do plano e focos no eixo Ox. Desta forma, sua equação reduzida é dada por:

Se os focos estiverem sobre o eixo Oy e centro na origem, a equação reduzida será igual a:

Parábola

Quando um plano intercepta um cone com uma inclinação paralela a uma de suas geratrizes, a figura que surge é uma parábola.

Sendo assim, a parábola é o lugar geométrico dos pontos pertencentes a um plano, que são equidistantes de uma reta fixa e de um ponto fixo.

Esse ponto fixo é chamado de foco da parábola e a reta recebe o nome de diretriz. A reta que passa pelo foco, perpendicular a diretriz, é chamada de eixo de simetria da parábola.

O vértice é o ponto de intersecção entre a parábola e o seu eixo, sendo que a distância entre o vértice e o foco é igual à distância do vértice a reta diretriz.

Equações reduzidas da parábola

Representando uma parábola em um plano cartesiano com o vértice coincidindo com a origem dos eixos e considerando c igual à distância entre o foco e o vértice, temos 4 situações possíveis.

1º) Eixo de simetria coincidente com o eixo Oy e reta diretriz y = - c, a equação será: x² = 4 cy.

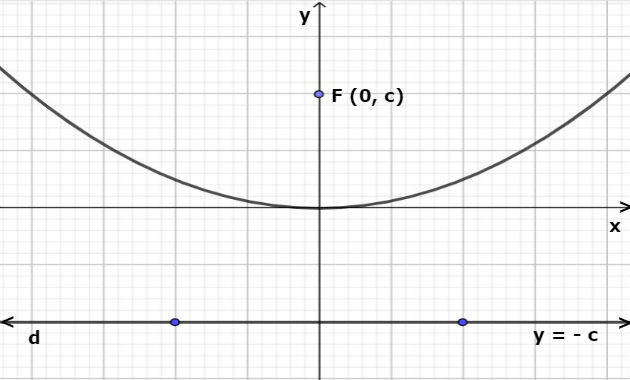
2º) Eixo de simetria coincidente com o eixo Ox e reta diretriz x = - c, a equação será: y² = 4 cx.

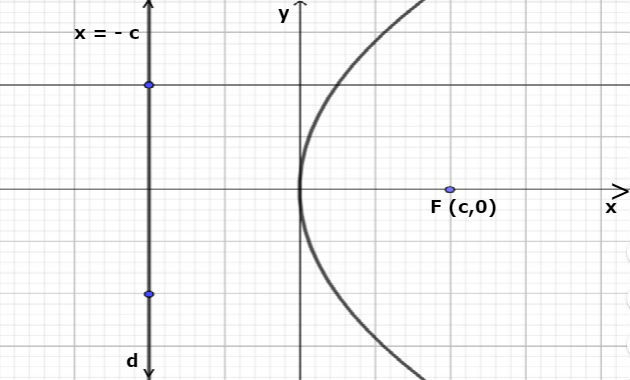
3º) Eixo de simetria coincidente com o eixo Oy e reta diretriz y = c, a equação será: x² = - 4 cy.

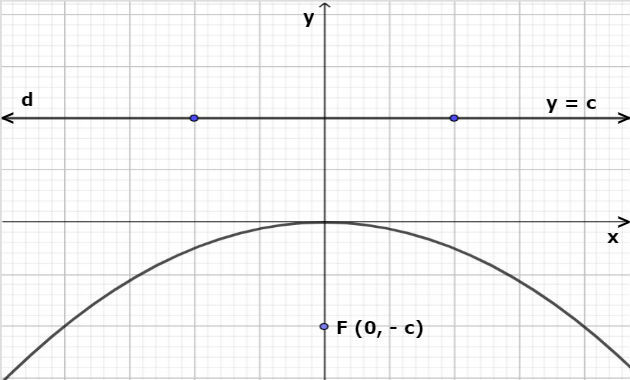
4º) Eixo de simetria coincidente com o eixo Ox e reta diretriz x = c, a equação será: y² = - 4 cx.

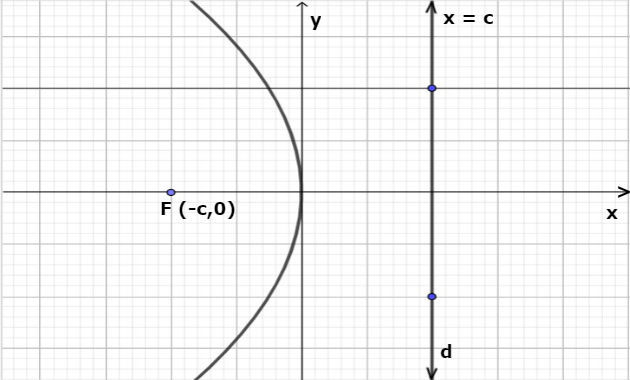
Hipérbole

Hipérbole é o nome da curva que surge quando um cone duplo é interceptado por um plano paralelo ao seu eixo.

Assim, a hipérbole é o lugar geométrico dos pontos no plano cujo módulo da diferença das distâncias a dois pontos fixos do plano (foco) é um valor constante.

A diferença das distâncias d₁ e d₂ é indicada por 2a, ou seja, 2a = | d₁ - d₂ |, e a distância entre os focos é dada por 2c, sendo que 2a < 2c.

Representando a hipérbole no eixo cartesiano, temos os pontos A₁ e A₂ que são os vértices da hipérbole. A reta que liga esses dois pontos é chamada de eixo real.

Temos ainda indicado os pontos B₁ e B₂ que pertencem à mediatriz da reta e que liga os vértices da hipérbole. A reta que liga esses pontos é chamada de eixo imaginário.

A distância do ponto B₁ à origem do eixo cartesiano é indicada, na figura, por b e é tal que b² = c² - a² .

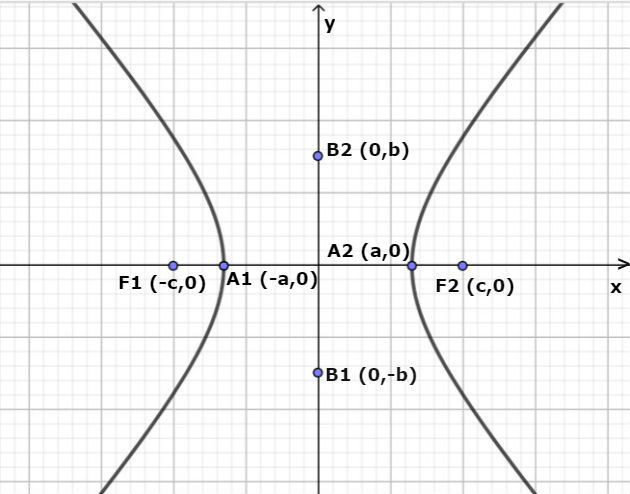
Equação reduzida hipérbole

A equação reduzida da hipérbole com os focos localizados no eixo Ox e o centro na origem é dada por:

Caso os focos estejam sobre o eixo Oy e centro também na origem, a equação será:

Aprenda mais sobre Geometria analítica.

Exercícios sobre cônicas

Exercício 1

(Enem - 2015) A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.

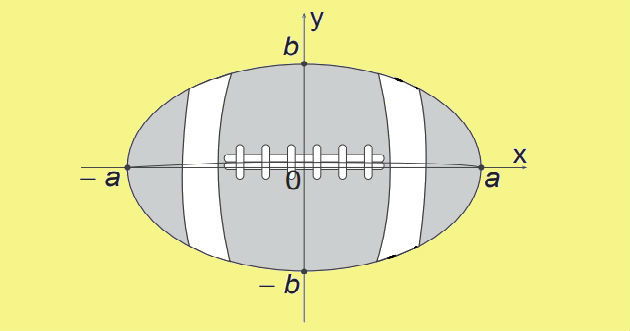
Considere que o volume aproximado dessa bola é dado por V = 4ab² . O volume dessa bola, em função apenas de b, é dado por

a) 8b³
b) 6b³
c) 5b³
d) 4b³
e) 2b³

Exercício 2

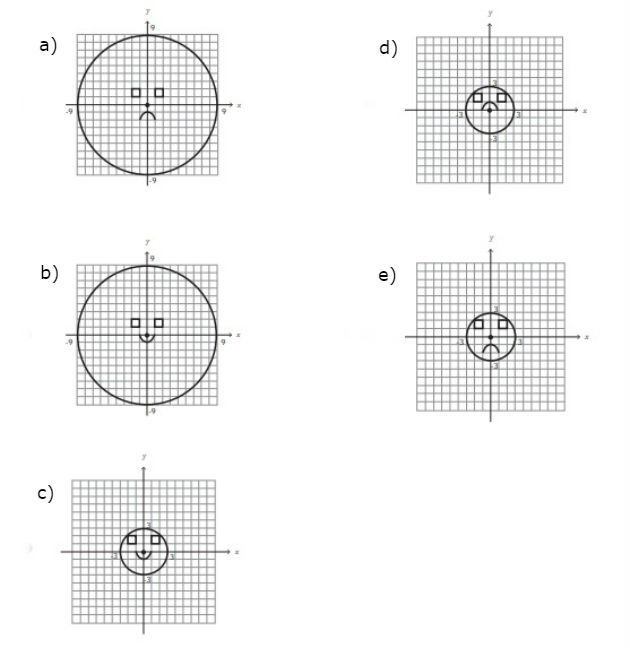
(Enem - 2013) Durante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:

I — é a circunferência de equação x² + y² = 9;
II — é a parábola de equação y = − x² − 1, com x variando de −1 a 1;
III — é o quadrado formado pelos vértices (−2, 1), (−1, 1), (−1, 2) e (−2, 2);
IV — é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
V — é o ponto (0, 0).

A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura.

Qual destas figuras foi desenhada pelo professor?

[LEITURA-RELACIONADA=3594 "Equação da Reta"
Veja também vértice da parábola.