Diagrama de Venn: o que é, operações entre conjuntos

Os diagramas de Venn são representações gráficas usadas para ilustrar elementos e relações entre conjuntos. Eles são amplamente utilizados na matemática, especialmente na Teoria dos Conjuntos, além de áreas como lógica e estatística.

Essas representações utilizam formas geométricas fechadas, geralmente círculos, elipses e retângulos.

Os elementos de cada conjunto são posicionados dentro dessas figuras, e a interseção ou sobreposição entre elas indica os elementos que pertencem a mais de um conjunto.

Para representar o conjunto universo, que engloba todos os elementos, é comum utilizar um retângulo. Já os subconjuntos do conjunto universo são representados por círculos que contêm os elementos de cada conjunto.

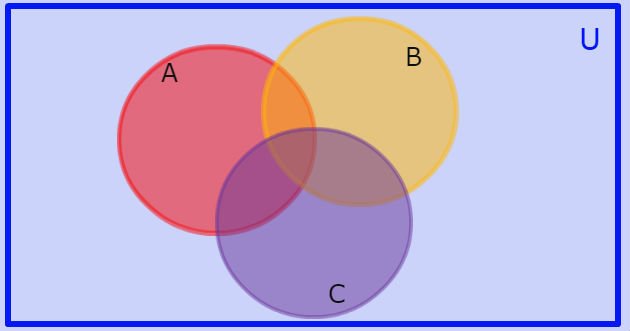
O diagrama de Venn recebe esse nome em homenagem ao matemático britânico John Venn (1834-1923) e foi concebido para representar operações entre conjuntos.

Além de ser aplicado em conjuntos, o diagrama de Venn é empregado nas mais diversas áreas do conhecimento como, por exemplo, lógica, estatística, ciências da computação, ciências sociais, entre outras.

Relação de inclusão entre conjuntos

Quando todos os elementos de um conjunto A também são elementos de um conjunto B, dizemos que o conjunto A é subconjunto de B, ou seja, o conjunto A é parte do conjunto B.

Indicamos este tipo de relação por e lemos "A está contido em B". Podemos usar ainda que representa "B contém A".

Para representar a relação de inclusão através do diagrama de Venn, colocamos um círculo dentro de outro, indicando que um conjunto é subconjunto do outro.

Exemplo

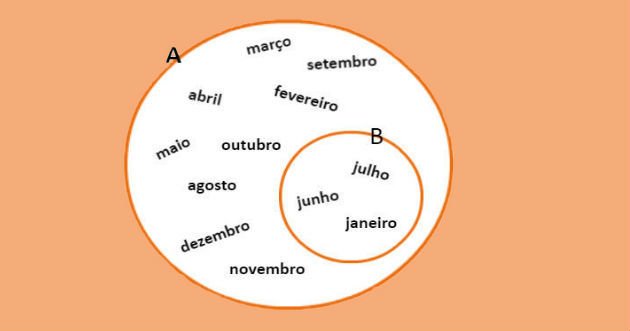
O conjunto B dos meses do ano que começam com a letra J é um subconjunto do conjunto A dos meses do ano. Assim, podemos representar esses conjuntos através do diagrama de Venn, conforme imagem abaixo:

Operações entre conjuntos

As principais operações incluem: diferença, união, interseção e complemento. Essas operações são visualizadas por meio de áreas sobrepostas ou separadas nos diagramas, facilitando a compreensão de como os conjuntos se relacionam entre si.

Diferença

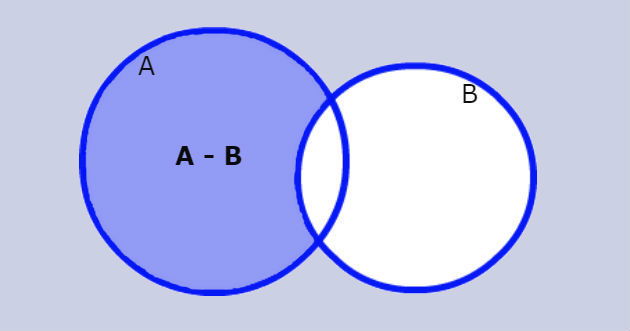
A diferença entre dois conjuntos corresponde a operação de escrever um conjunto eliminando os elementos que também fazem parte de outro.

Essa operação é indicada por A - B. O resultado são os elementos que pertencem a A, mas que não pertencem a B.

Para representar esta operação através do diagrama de Venn, desenhamos dois círculos e pintamos um deles, excluindo a parte em comum dos conjuntos.

União

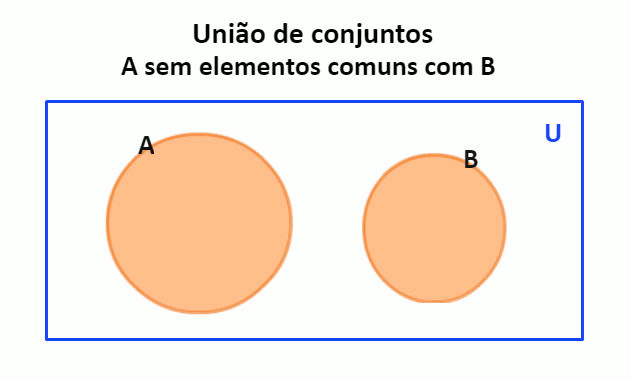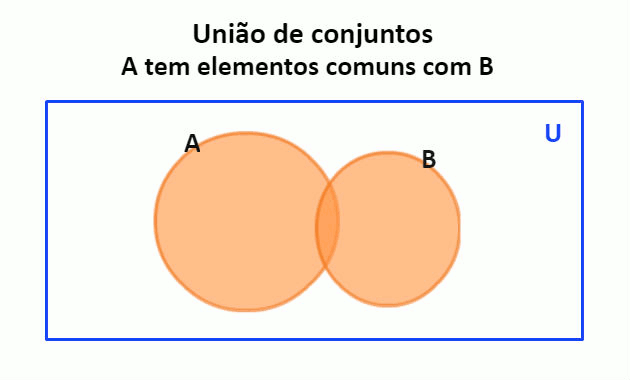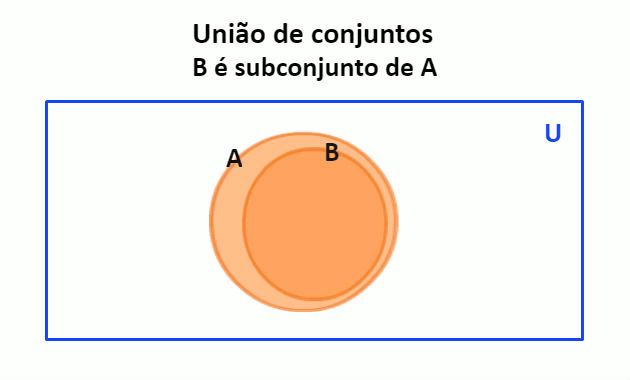
A operação de união representa a junção de todos os elementos que pertencem a dois ou mais conjuntos. Para indicar essa operação usamos o símbolo . São os elementos que pertencem a A, B, ou ambos.

No diagrama de Venn essa operação é indicada pintando toda parte interna das áreas que representam os conjuntos.

Interseção

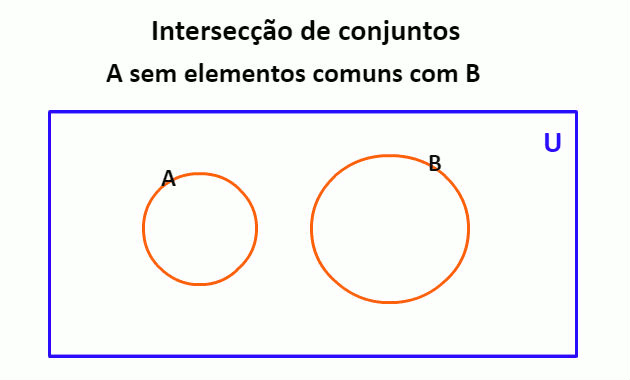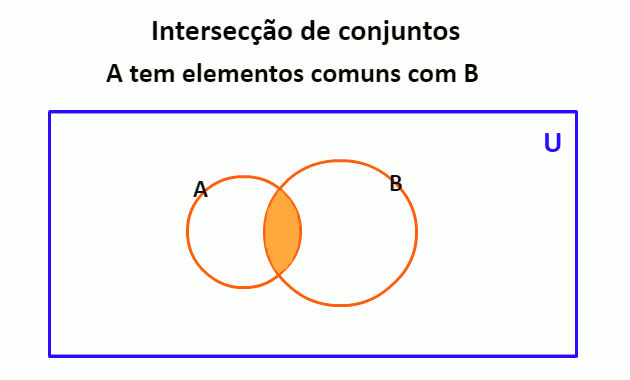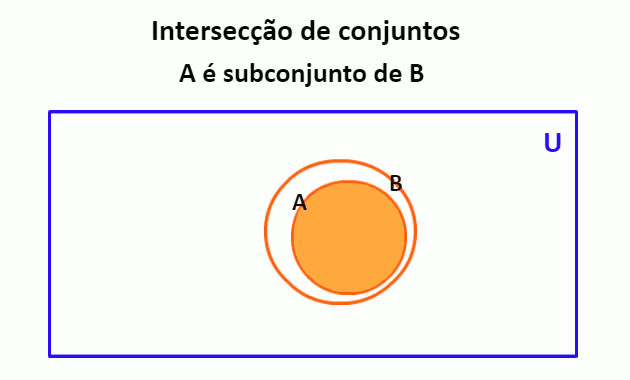
A interseção entre conjuntos é o conjunto de elementos que pertencem simultaneamente a dois ou mais conjuntos.

Assim, dados dois conjuntos A e B, a interseção entre eles será denotada por e indicada no diagrama de Venn pela pintura da parte comum.

Complemento

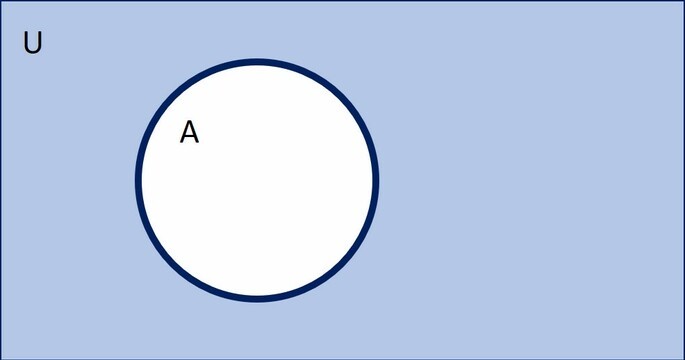
O complemento de um conjunto A é o conjunto de elementos que pertencem ao universo, mas não a A.

É comum representar o complemento de um conjunto com um pequeno c acima: .

Quantidade de elementos de um conjunto

O diagrama de Veen é uma ótima ferramenta para ser usada em problemas que envolvam reunião de conjuntos.

Através do uso do diagrama, fica mais fácil identificar as partes comuns (interseção) e assim, descobrir a quantidade de elementos da união.

Exemplo

Foi feita uma pesquisa entre 100 estudantes de uma escola sobre o consumo de três marcas de refrigerantes: A, B e C. O resultado obtido foi: 38 estudantes consomem a marca A, 30 a marca B, 27 a marca C; 15 consomem a marca A e B, 8 as marcas B e C, 19 as marcas A e C e 4 consomem os três refrigerantes.

Considerando os dados da pesquisa, quantos estudantes consomem apenas uma dessas marcas?

Resolução

Para resolver esse tipo de questão, vamos começar desenhando um diagrama de Venn. Cada marca de refrigerante será representada por um círculo.

Vamos começar colocando o número de estudantes que consomem as três marcas simultaneamente, ou seja, a interseção da marca A, B e C.

Note que o número que consome as três marcas também está embutido no número que consome duas marcas. Então, antes de colocar esses valores no diagrama devemos tirar esses estudantes em comum.

Devemos fazer o mesmo para o número que consome cada marca, pois aí também está repetido as partes comuns. Todo esse processo está apresentado na imagem abaixo:

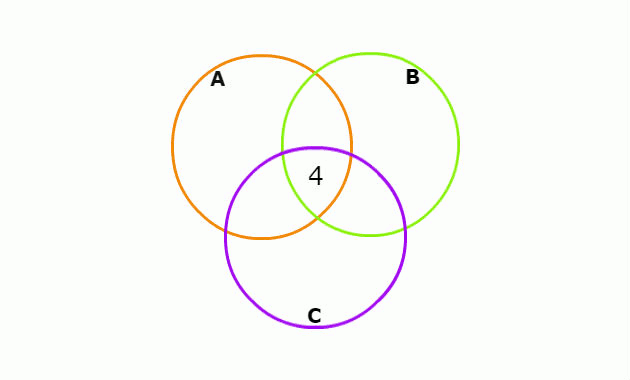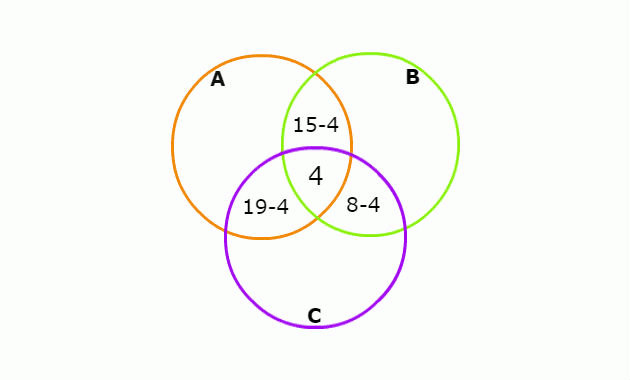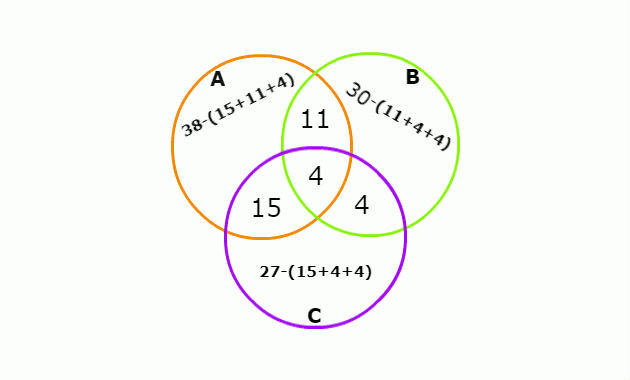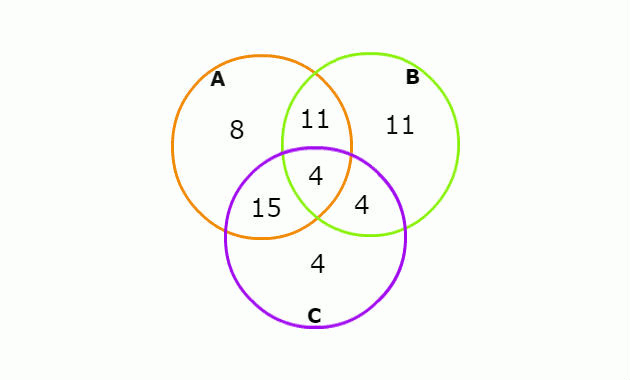
Agora que conhecemos o número de cada parte do diagrama, podemos calcular o número de estudantes que consome apenas uma dessas marcas, somando os valores de cada conjunto. Assim, temos:

Nº de pessoas que consome apenas uma das marcas = 11 + 8 + 4 = 23

Exercícios sobre diagramas de Venn

Exercício 1

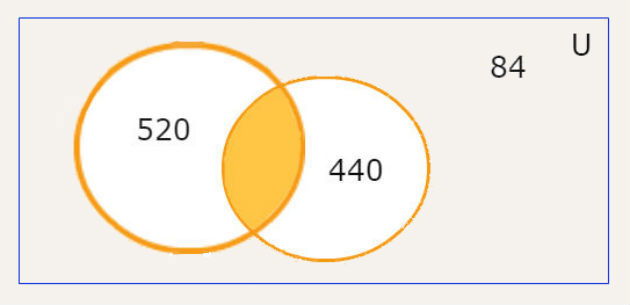
(UERJ - 2015) Em uma escola circulam dois jornais: Correio do Grêmio e O Estudante. Em relação à leitura desses jornais, por parte dos 840 alunos da escola, sabe-se que:

• 10% não leem esses jornais;
• 520 leem o jornal O Estudante;
• 440 leem o jornal Correio do Grêmio.

Calcule o número total de alunos do colégio que leem os dois jornais.

Exercício 2

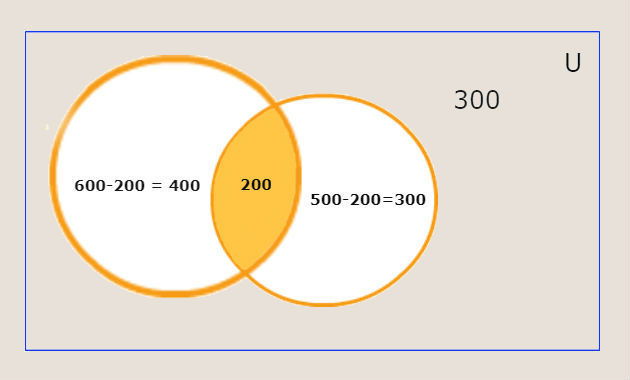
(Enem - 2013) Numa escola com 1200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras, inglês e espanhol.

Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.

Escolhendo-se um aluno dessa escola ao acaso e sabendo-se que ele não fala inglês, qual a probabilidade de que esse aluno fale espanhol?

Veja também exercícios sobre conjuntos.