Dinâmica: entenda o que é, os conceitos e fórmulas (com exercícios)
A dinâmica é a parte da física que estuda a origem dos movimentos dos corpos.
As principais leis utilizadas nos estudos da dinâmica dos corpos foram formuladas por Isaac Newton. De forma geral, essas leis atestam que as forças são responsáveis pela variação dos estados de repouso ou de movimento dos corpos. Elas são suficientes tanto para descrever quanto para prever o comportamento de qualquer sistema da mecânica clássica.
Vamos iniciar nosso estudo da dinâmica com as três Leis de Newton. Depois, usaremos essas leis na discussão de cinco exemplos, que visam compreender as leis em si e também a atuação das forças na definição dos movimentos dos corpos.
Ao final teremos quatro questões de múltipla escolha com gabaritos explicados, para você verificar sua aprendizagem.
As Leis de Newton e suas fórmulas
As leis de Isaac Newton foram publicadas em 1687 em seu estudo Philosophiae Naturalis Principia Mathematica. São elas:
Primeira Lei ou Lei da inércia
Um corpo em repouso ou em movimento retilíneo uniforme permanecerá nesse estado de repouso ou de movimento se sobre ele não atuar nenhuma força ou se a força resultante que atua sobre ele for nula.
A força resultante é a soma vetorial de todas as forças que atuam sobre o corpo.
Segunda Lei ou Lei Fundamental da Dinâmica
A mudança de movimento de um corpo é proporcional à força resultante que atua sobre ele, e se dá na direção da força resultante.
A segunda lei é representada pela fórmula:
onde é a força resultante que atua no corpo, que é igual à soma vetorial de todas as forças que atuam no corpo.
m é a massa do corpo e é a aceleração resultante adquirida pelo corpo.
Newton define força como "uma ação exercida sobre um corpo que altera seu estado de repouso ou de movimento retilíneo uniforme". Sua segunda lei quantifica a relação entre força e movimento, através do vetor aceleração do corpo.
Terceira Lei ou Lei da Ação e Reação
A cada ação opõe-se sempre uma reação igual, ou em outras palavras, as ações mútuas de dois corpos são sempre iguais e dirigidas a partes contrárias.
Essa lei é representada pela equação quando temos dois corpos A e B
onde
é a força exercida no corpo B pelo corpo A e
é a força exercida no corpo A pelo corpo B.
Aplicando as leis de Newton (exemplos)
Como as leis de Newton são vetoriais, vamos primeiro fazer uma rápida revisão da soma de vetores, centrando na determinação da força resultante.
A tabela abaixo traz diferentes possibilidades de somas vetoriais.
|
Corpo de massa m Forças atuantes |
Determinação da força resultante, |
Representação da força resultante |
|---|---|---|
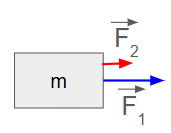 |
As duas forças possuem mesma direção e sentido. Assim, a força resultante terá a mesma direção e o mesmo sentido. Seu módulo será dado pela soma algébrica das duas forças ou |
 |
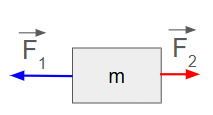 |
As duas forças possuem mesma direção, mas sentidos opostos. A força resultante terá a mesma direção, mas seu sentido será o mesmo da força de maior intensidade. Seu módulo será dado pela subtração algébrica das duas forças ou |
 |
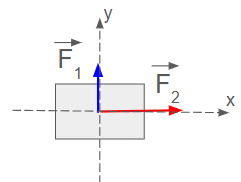 |
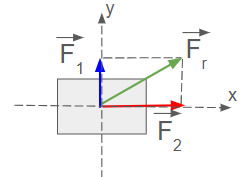
As duas forças são perpendiculares. Nesse caso é preciso usar o Teorema de Pitágoras para determinar o módulo da força resultante ou |
 |
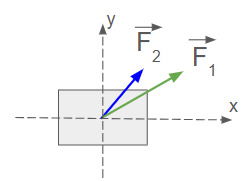 |
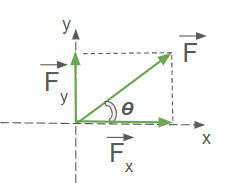
As duas forças estão em ângulo com o eixo x,y. Nesse caso cada uma das forças terá que ser decomposta em seus componentes Na figura abaixo mostramos como decompor cada força:
Pela lei dos senos e cossenos, vem: |
As componentes x e y da força resultante serão: E seu módulo será: |
Exemplo 1
Um corpo de massa m = 5kg está sujeito a uma força horizontal para a direita de módulo 2N e a uma força horizontal de módulo 2N para a esquerda. Qual é o estado desse corpo?
Resolução:
Para determinar o estado do corpo precisamos saber qual é a força resultante. Vamos primeiro representar o problema com um desenho.
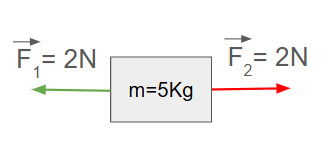
Como as forças possuem mesma direção, mas sentidos opostos, o módulo da força resultante é dado pela diferença entre elas. Assim
, ou seja, a força resultante é nula.
Se a força resultante é nula, temos que a aceleração do corpo também será nula, pois pela Segunda Lei de Newton temos:
que nesse caso fica:
ou a = 0 m/s2
Pela Lei da Inércia, esse corpo estará parado ou se movimentando em movimento retilíneo uniforme, visto que sua aceleração é nula.
Exemplo 2
Um corpo de massa igual a 1kg está sujeito a duas forças horizontais, uma para a direita de intensidade 17N e outra para a esquerda de intensidade F2. Quais devem ser o sentido e o módulo de F2 para esse corpo permanecer em repouso?
Resolução:
O primeiro passo é representar o sistema por meio de um desenho. Nesse caso o esquema é:
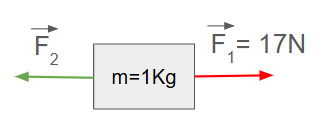
A Lei da Inércia diz que um corpo permanece em repouso ou em movimento retilíneo uniforme se a força resultante que atua sobre ele for nula.
Então temos:
O sinal negativo no valor de F2 indica que ela tem sentido contrário à F1. Como o sentido de F1 é para a direita, o sentido de F2 é para a esquerda (como representado no desenho acima).
Exemplo 3
Qual é a aceleração de um corpo de massa 3Kg sujeito à duas forças de mesma direção, sentido e módulos iguais a 11N e 7N?
Resolução:
O primeiro passo é representar o sistema por meio de um desenho:
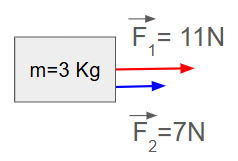
O segundo passo é determinar a força resultante.
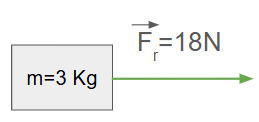
Usamos agora a Segunda Lei de Newton para determinar o valor da aceleração.
A aceleração tem direção horizontal, sentido para direita e módulo igual a 6m/s2.
Exemplo 4
Determine a aceleração do movimento de um corpo de massa 5 kg que cai de uma altura de 10 m sob a ação de seu peso em um local onde a resistência do ar é igual a 5N. Considere que a aceleração da gravidade é igual a 10 m/s2.
Resolução:
O primeiro passo é representar o problema por um desenho:
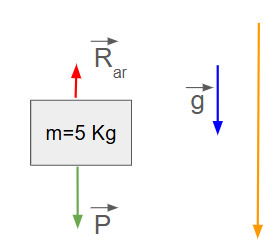
A direção do movimento é para baixo (flecha laranja), visto que o enunciado disse que o corpo cai. A aceleração da gravidade também é para baixo (flecha azul), já que ela aponta na direção do centro do planeta.
O próximo passo é determinar o peso do corpo. Sabendo que P = m.g temos P = 5.10 = 50N.
Agora determinamos a força resultante
As forças que estão na mesma direção do movimento entram na equação com sinal positivo. Já as que são opostas à direção do movimento entram com sinal negativo. Assim:
Aplicando a Segunda Lei de Newton, vem:
Observe que o corpo cai com aceleração menor do que a aceleração da gravidade. Isso acontece por conta da força de resistência do ar.
Exemplo 5
Um corpo de massa igual a 20 Kg que está em repouso sobre a superfície de uma mesa horizontal está sujeito à força peso. Por que esse corpo não cai?
Resolução:
Vamos primeiro representar o problema:
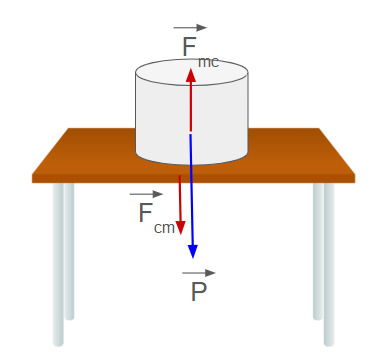
A força peso é devida à interação do corpo com o planeta.
Como o corpo está apoiado na mesa, ele empurra a mesa para baixo com uma força que é a força do corpo (c) aplicada sobre a mesa (m). Essa força é exatamente igual ao peso do corpo ou
Pela Terceira Lei de Newton temos que a mesa reage e aplica sobre o corpo uma força igual em sentido oposto ou que é a força da mesa (m) no corpo (c). Essa força, que tem módulo igual ao peso do corpo, é chamada de força normal e representada por
. Temos que
onde o sinal negativo indica que os sentidos da força peso e da força normal são opostos.
Como o corpo não se movimenta, a força resultante que atua sobre ele é nula segundo a Primeira Lei de Newton. Assim temos que os módulos de e do peso
são iguais, ou seja,
.
Questões sobre dinâmica
Resolva os problemas a seguir para verificar sua aprendizagem.
Questão 1
Classifique cada um dos enunciados das Leis de Newton como Falso (F) ou Verdadeiro (V) e depois escolha a alternativa correta.
I. Lei da Inércia - um corpo permanece em seu estado de repouso ou de movimento contínuo quando a força resultante sobre ele for nula.
II. Segunda Lei - A força resultante sobre um corpo é igual ao produto da massa do corpo pela aceleração resultante.
III. Lei da Ação e Reação - se um corpo A imprime uma força sobre um corpo B, o corpo B reage imprimindo sobre o corpo A uma força de mesma direção, mesma intensidade mas de sentido oposto.
a) V, V, V.
b) F, F, F.
c) F, V, F.
d) F, V, V.
Resposta correta: alternativa d) F, V, V.
A frase I está errada pois fala em "movimento contínuo" e não em movimento retilíneo uniforme.
Questão 2
As forças de ação e de reação se anulam ou não? Por quê?
a) Elas se anulam porque elas estão aplicadas em corpos distintos.
b) Elas não se anulam porque estão aplicadas em corpos distintos.
c) Elas se anulam porque estão aplicadas em um único corpo.
d) Elas não se anulam porque estão aplicadas em um único corpo.
Resposta correta: alternativa b) Elas não se anulam porque estão aplicadas em corpos distintos.
A terceira lei de Newton atesta que se um corpo A imprimi uma força sobre um corpo B, o corpo B reage e imprimi no corpo A uma força de mesma direção e intensidade, mas com sentido oposto. Isso explica porque as forças de ação e reação não se anulam, porque elas estão aplicadas em corpos distintos.
Questão 3
Para praticar: Exercícios sobre dinâmica na Física (com gabarito explicado)
Para estudar mais: Leis de Newton: 1ª, 2ª e 3ª Lei de Newton (com exercícios) e Cinemática: conceito e fórmulas
Se você está no 1º ano do Ensino Médio, este conteúdo vai te ajudar: Introdução à Física: entenda o que é e todos os principais conceitos
Referências Bibliográficas
Chibeni, S.S. A Fundamentação Empírica das Leis Dinâmicas de Newton Revista Brasileira de Ensino de Fsica, vol. 21, no. 1, Marco, 1999. Acesso em 24/02/2025.
Iliffe, R., Mandelbroate, S. The Newton Project. Acesso em 24/02/2025.
SOUTO, Ana. Dinâmica: entenda o que é, os conceitos e fórmulas (com exercícios). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/dinamica-entenda-o-que-e-os-conceitos-e-formulas-com-exercicios/. Acesso em: