Distância entre dois pontos: como calcular e exemplos

Revisão por Rafael C. Asth

Professor de Matemática e Física

A distância entre dois pontos é o comprimento medido em linha reta que separa dois locais. Ela é representada pelo segmento de reta que liga essas duas regiões no espaço. Por ser uma medida linear, é geralmente expressa em unidades como metros ou centímetros.

Essa distância é uma maneira de quantificar o 'espaço' entre dois lugares, como se você quisesse saber a distância entre duas casas em um mapa.

Na matemática, fazemos isso semelhantemente, usando um sistema de coordenadas numéricas (como se fossem endereços exatos) para calcular a distância entre dois pontos.

Se os pontos estiverem em um plano, como em uma folha de papel, utilizamos uma fórmula que envolve duas coordenadas. Se os pontos estiverem no espaço tridimensional, como no mundo real, o princípio é o mesmo, mas adicionamos uma terceira coordenada para representar a altura.

Essas posições ou 'endereços' são representados por duas coordenadas, x e y, formando o que chamamos de par ordenado, representado como (x, y). A coordenada x é conhecida como abscissa, e a coordenada y é chamada de ordenada.

Em resumo, calcular a distância entre dois pontos é só uma maneira mais precisa de dizer qual é a distância “daqui até lá”, mas usando números, fórmulas e unidades de medida.

Podemos fazer o cálculo dessa medida usando conceitos de uma área da Matemática chamada de Geometria Analítica.

Fórmula da distância entre dois pontos no plano

A fórmula que nos permite calcular a distância entre dois pontos no plano e utiliza as medidas x e y é:

$começar estilo tamanho matemático 18px reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo reto x com reto A subscrito menos reto x com reto B subscrito parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto y com reto A subscrito menos reto y com reto B subscrito parêntese direito ao quadrado fim da raiz fim do estilo$

Os índices A e B logo abaixo de x e y se referem a estas medidas para os pontos A e B.

Repare que a ordem dos termos das subtrações entre parenteses não alteram o resultado, pois o resultado está elevado ao quadrado, retornando sempre um valor positivo.

Imagine que você tem dois pontos em um papel e quer saber a distância entre eles. Uma maneira simples de fazer isso é desenhar um triângulo retângulo. A linha que liga os dois pontos é a hipotenusa (parte mais longa do triângulo). As outras duas linhas do triângulo, que são perpendiculares entre si, são chamadas de catetos.

Para calcular a distância entre os dois pontos, o que fazemos é descobrir o comprimento desses dois catetos, sendo as diferenças entre as medidas de x e de y para cada ponto, ou seja, os termos $começar estilo tamanho matemático 14px texto x fim do texto com reto A subscrito menos reto x com reto B subscrito fim do estilo$ e $começar estilo tamanho matemático 14px reto y com reto A subscrito menos reto y com reto B subscrito fim do estilo$ na fórmula.

O termo $reto d parêntese esquerdo reto A vírgula reto B parêntese direito$ é a hipotenusa do triângulo. Perceba que a fórmula para o cálculo da distância entre dois pontos é uma aplicação do Teorema de Pitágoras.

Exemplos de cálculo da distância entre dois pontos resolvidos

Exemplo 1

Suponha que o mapa abaixo represente o bairro de Ana (ponto A) e Bruno (ponto B). Se os pontos no mapa representam a localização de suas casas, qual a distância entre elas?

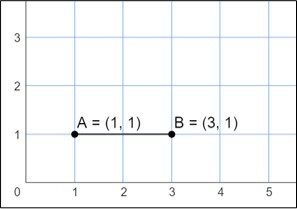
Neste caso, as ordenadas (pontos referentes ao eixo y) são iguais. Eles estão em mesma “altura” no mapa. A distância pode ser calculada apenas pela subtração entre as abscissas de A e de B.

d(A,B) = 3 - 1 = 2

Exemplo 2

Ainda no mesmo bairro de Ana e Bruno, também mora Carlos, que tem a localização de sua casa indicada no mapa no ponto C.

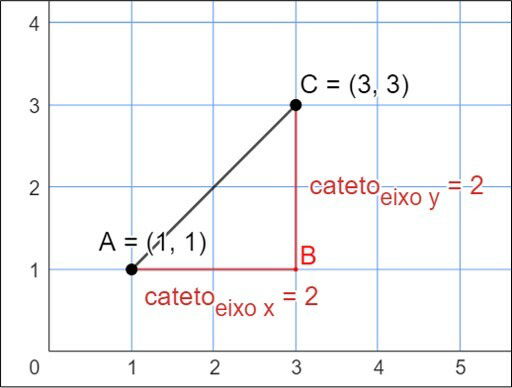
Note que a distância entre o ponto A e o ponto C é igual à hipotenusa do triângulo retângulo de catetos 2 e 2.

$reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 2 ao quadrado mais 2 ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 4 mais 4 fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 8 reto d parêntese esquerdo reto A vírgula reto B parêntese direito aproximadamente igual 2 vírgula 8 espaço unidades$

Para saber mais, leia também:

Exercícios resolvidos sobre distância entre dois pontos

Exercício 1

A cidade de Arvoredo tem dois marcos históricos importantes: a Praça Central, localizada no ponto A(3,4), e a Torre do Relógio, situada no ponto B(7,1) no mapa da cidade, representado em um plano cartesiano.

O departamento de turismo da cidade quer colocar placas informativas que indiquem a distância exata entre esses dois marcos. A distância, em unidades de mapa, que será informada é de

a) 3 unidades.
b) 4 unidades.
c) 5 unidades.
d) 6 unidades.
e) 7 unidades.

Ver Resposta

Resposta correta: c) 5 unidades.

Utilizando a fórmula da distância entre dois pontos e substituindo os valores:

$começar estilo tamanho matemático 16px reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo reto x com reto A subscrito menos reto x com reto B subscrito parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto y com reto A subscrito menos reto y com reto B subscrito parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo 3 menos 7 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 4 menos 1 parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo menos 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 3 parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 16 espaço mais espaço 9 fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 25 reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a 5 fim do estilo$

Assim, a distância, em unidades de mapa, que será informada é de 5 unidades.

Exercício 2

Um ponto A pertence ao eixo das abscissas (eixo x) e é equidistante dos pontos B (3,2) e C (-3,4). Quais são as coordenadas do ponto A?

Ver Resposta

Como o ponto A pertence ao eixo das abscissas, sua ordenada y é 0. Assim, podemos escrever A como A(x, 0).

O próximo passo é encontrar a distância de A até B:

O ponto B tem coordenadas B(3 ,2).

A distância entre A e B é dada por:

$reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo reto x menos 3 parêntese direito ao quadrado mais parêntese esquerdo 0 menos 2 parêntese direito ao quadrado fim da raiz espaço$

Calculando o quadrado do segundo termo:

$reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo reto x menos 3 parêntese direito ao quadrado mais 4 fim da raiz$

O próximo passo é calcular a distância de A até C:

O ponto C tem coordenadas C(−3, 4).

A distância entre A e C é dada por:

$reto d parêntese esquerdo AC parêntese direito igual a raiz quadrada de parêntese esquerdo reto x menos parêntese esquerdo menos 3 parêntese direito parêntese direito ao quadrado espaço mais parêntese esquerdo 0 menos 4 parêntese direito ao quadrado espaço fim da raiz reto d parêntese esquerdo AC parêntese direito igual a raiz quadrada de parêntese esquerdo reto x mais 3 parêntese direito ao quadrado espaço mais parêntese esquerdo 0 menos 4 parêntese direito ao quadrado espaço fim da raiz reto d parêntese esquerdo AC parêntese direito igual a raiz quadrada de parêntese esquerdo reto x mais 3 parêntese direito ao quadrado espaço mais parêntese esquerdo menos 4 parêntese direito ao quadrado espaço fim da raiz$

Calculando o quadrado do segundo termo:

$reto d parêntese esquerdo AC parêntese direito igual a raiz quadrada de parêntese esquerdo x mais 3 parêntese direito ao quadrado mais 16 fim da raiz espaço espaço$

Sabemos que o ponto A é equidistante dos pontos B e C, logo d(A, B) = d(A, C).

Igualando as duas expressões:

$raiz quadrada de parêntese esquerdo x menos 3 parêntese direito ao quadrado espaço mais 4 fim da raiz espaço igual a raiz quadrada de espaço parêntese esquerdo x mais 3 parêntese direito ao quadrado espaço mais 16 fim da raiz espaço espaço$

A próxima etapa da equação consiste em eliminar as raízes quadradas.

Elevamos ambos os lados ao quadrado anulando as raízes:

$abre parênteses raiz quadrada de parêntese esquerdo x menos 3 parêntese direito ao quadrado mais 4 fim da raiz fecha parênteses ao quadrado igual a abre parênteses raiz quadrada de parêntese esquerdo x mais 3 parêntese direito ao quadrado espaço mais 16 fim da raiz fecha parênteses ao quadrado parêntese esquerdo x menos 3 parêntese direito ao quadrado mais 4 espaço igual a parêntese esquerdo x mais 3 parêntese direito ao quadrado espaço mais 16$

Expandindo os quadrados:

$parêntese esquerdo x ao quadrado menos 6 x mais 9 parêntese direito mais 4 igual a parêntese esquerdo x ao quadrado mais 6 x mais 9 parêntese direito mais 16$

Simplificando:

$x ao quadrado espaço menos 6 x mais 13 igual a x ao quadrado mais 6 x mais 25$

Eliminamos o x² de ambos os lados:

$menos 6 x mais 13 igual a 6 x mais 25$

Isolando x:

$menos 6 x menos 6 x igual a 25 mais 13 menos 12 x igual a 38 x igual a numerador 38 sobre denominador menos 12 fim da fração x igual a menos 19 sobre 6$

Assim, a coordenada do ponto A é $abre parênteses menos 19 sobre 9 vírgula espaço 0 fecha parênteses$ .

Distância entre dois pontos no espaço tridimensional

Usamos um sistema de coordenadas tridimensional para representar pontos no espaço, acrescentando um eixo, perpendicular aos do plano.

Todo ponto fica totalmente determinado no espaço quando existe uma tripla coordenada (x,y,z) associado a ele.

Para encontrar a distância entre dois pontos no espaço o cálculo segue os mesmos princípios utilizados para o plano: o Teorema de Pitágoras. A única diferença é que para o espaço, a fórmula apresente uma terceira parcela.

Fórmula da distância entre dois pontos no espaço tridimensional

Exemplo

Dois helicópteros estão parados no ar em determinado instante. Um controlador de voo, na base, comunica-se com os pilotos, fornecendo-lhes suas coordenadas em relação à base, sendo considerada o ponto zero (0, 0, 0) de um sistema cartesiano tridimensional.

A localização do helicóptero C é (3, 1, 4), enquanto a do helicóptero D é (4, 2, 2), com essas medidas expressas em quilômetros. O operador realizou os cálculos e informou aos pilotos a distância entre eles nesse momento.

Determine a distância entre os helicópteros indicada pelo controlador de voo.

Resolução

$reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo reto x com reto A subscrito menos reto x com reto B subscrito parêntese direito ao quadrado mais parêntese esquerdo reto y com reto A subscrito menos reto y com reto B subscrito parêntese direito ao quadrado mais parêntese esquerdo reto z com reto A subscrito menos reto z com reto B subscrito parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo 3 menos 4 parêntese direito ao quadrado mais parêntese esquerdo 1 menos 2 parêntese direito ao quadrado mais parêntese esquerdo 4 menos 2 parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de parêntese esquerdo menos 1 parêntese direito ao quadrado mais parêntese esquerdo menos 1 parêntese direito ao quadrado mais parêntese esquerdo 2 parêntese direito ao quadrado fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 1 mais 1 mais 4 fim da raiz reto d parêntese esquerdo reto A vírgula reto B parêntese direito igual a raiz quadrada de 6 reto d parêntese esquerdo reto A vírgula reto B parêntese direito aproximadamente igual 2 vírgula 449$

Logo, a distância entre os helicópteros é de 2,449 km.

Para saber mais, leia também:

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações