Estática: entenda o que é e as fórmulas (com exercícios resolvidos)

Rafael C. Asth

Professor de Matemática e Física

A Estática, ramo da Física, estuda sistemas em equilíbrio, ou seja, em repouso. Ela analisa as condições necessárias para que corpos ou sistemas permaneçam estáveis sob a ação de forças.

O termo “estática” vem do grego statikós, que significa “equilíbrio” ou “estabilidade”. Esse conceito é essencial em áreas como engenharia e arquitetura, sendo aplicado no funcionamento de pontes, edifícios, guindastes e até no equilíbrio do corpo humano.

A Estática foca no equilíbrio mecânico, abrangendo o estudo de materiais em dois estados principais: corpos rígidos (sólidos) e fluidos (gases ou líquidos).

Estática dos sólidos

A Estática dos sólidos analisa a ação de forças em corpos extensos, considerados rígidos e indeformáveis, que se encontram em equilíbrio.

O equilíbrio dos corpos rígidos envolve a ausência de duas categorias de movimento: translação e rotação.

Translação refere-se ao deslocamento do corpo em relação a um referencial inercial. Quando esse movimento está ausente, o corpo não apresenta aceleração em relação ao referencial.

Para garantir essa condição, a soma vetorial de todas as forças atuantes sobre o corpo deve ser igual a zero.

⁣, ou seja:

Onde F são as forças aplicadas ao corpo.

Vale lembrar que a definição de somatório das forças que atuam no corpo é a mesma de força resultante da 2º Lei de Newton:

A força resultante ser zero implica que a aceleração é zero, ou seja, o corpo está em equilíbrio.

Os movimentos de rotação são caracterizados pelo giro de um corpo em torno de um ponto ou eixo de referência. Também chamados de torque (T) ou momento angular (M), a condição de equilíbrio estático exige que a soma dos torques seja igual a zero.

, ou seja:

Alguns conceitos são fundamentais para entender a estática dos sólidos, como o torque e o centro de massa.

Torque (ou momento angular): os giros

O torque mede a capacidade de uma força de fazer um objeto girar em torno de um ponto ou eixo. Ele depende da intensidade da força, do ângulo de aplicação e da distância entre o ponto de aplicação e o eixo de rotação.

A fórmula para calcular o torque é:

Onde:

• M é o torque, medido em (N . m);
• F é a força de aplicação, medida em (N)
• d é a distância do ponto de aplicação da força ao eixo de giro, medida em (m).

Observação: é comum o uso da letra T(torque) no lugar de M.

Exemplo: Torque no Aperto de um Parafuso

Imagine que você está trocando o pneu do seu carro porque ele furou. Para soltar o parafuso da roda, você utiliza uma chave de roda. O fabricante recomenda que o torque necessário para soltar o parafuso seja de 100 N·m.

Se você aplicar a força com as mãos no final de uma chave de roda de 50 cm de comprimento, qual deve ser a força mínima aplicada para conseguir soltar o parafuso?

Resolução:

Os dados fornecidos são o torque necessário para soltar o parafuso, de 100 Nm e o comprimento da chave, 50 cm ou 0,5 m.

Substituindo os valores na fórmula:

A força mínima que você precisa aplicar no final da chave de roda é de 200 N. Isso equivale a aproximadamente 20 kgf (a força aproximada necessária para levantar um peso de 20 kg com a gravidade terrestre).

Centro de massa: o equilíbrio em um ponto

O centro de massa é o "ponto de equilíbrio" de um objeto, onde toda a sua massa pode ser considerada concentrada. É um ponto fictício por onde a gravidade parece atuar, também conhecido como centro de gravidade.

Em sistemas de partículas ou corpos contínuos, o centro de massa representa o ponto onde a massa total pode ser tratada como concentrada para a análise do movimento.

Algumas propriedades do centro de massa:

1. O centro de massa é o ponto onde as forças externas, como a gravidade, podem ser consideradas aplicadas no estudo do movimento do corpo.
2. Para um corpo homogêneo de forma regular, o centro de massa coincide com o centro geométrico.
3. No caso de sistemas em equilíbrio, o centro de massa permanece fixo ou se move em linha reta se submetido a uma força externa.

Exercício resolvido: condição para estática de um sólido

Condições de Equilíbrio em uma Gangorra.

Imagine que você está em um parque de diversões brincando em uma gangorra que precisa ser equilibrada.

Uma criança de 30 kg está sentada a 2 metros do fulcro (ponto de apoio). Do outro lado, dois adolescentes estão sentados:

• O primeiro tem massa de 50 kg e está a 1 metro do fulcro.
• O segundo tem massa de 40 kg e pode se mover ao longo da gangorra.

Qual deve ser a distância do segundo adolescente ao fulcro para a gangorra permanecer estática?

Resolução:

Para a gangorra permanecer estática, a soma dos torques no sentido horário deve ser igual à soma dos torques no sentido anti-horário:

O torque é dado pela fórmula:

Onde F é a força em (N) e d é a distância do ponto de aplicação da força até o ponto de giro (fulcro).

As forças que atuam na gangorra são os pesos. A força peso é calculada por:

Forças Atuantes no Sistema:

Torques no Sistema:

Onde d é a distância pretendida.

Condição para a gangorra permanecer estática:

A haver equilíbrio, o somatório dos torques ou, momentos angulares, deve ser zero.

Adotando como positivos os giros no sentido horário e negativos os anti-horários:

Substituindo os valores:

Conclusão:

Para equilibrar a gangorra, o segundo adulto de 40 kg deve se sentar a 0,25 metros (25 cm) do fulcro.

Esse problema mostra como as condições de equilíbrio dependem da distribuição das forças e suas distâncias em relação ao ponto de apoio, sendo uma aplicação direta da estática dos sólidos no dia a dia.

Estática dos fluidos

A estática dos fluidos é o ramo da física que estuda os fluidos em repouso e as forças que eles exercem sobre as superfícies em contato.

Fluidos, como líquidos e gases, possuem propriedades específicas que influenciam seu comportamento em situações de equilíbrio.

Entender a estática dos fluidos é fundamental para diversas aplicações práticas, desde engenharia hidráulica até meteorologia.

Um fluido em repouso não possui movimento relativo entre suas partículas, o que significa que as forças que atuam nele estão em equilíbrio.

Dois conceitos importantes no estudo dos fluidos são a pressão e a densidade.

A pressão é uma grandeza que mede a força exercida por unidade de área.

Onde:

• P é a pressão (Pa);
• F é a força perpendicular à superfície, (N);
• A é a área da superfície (m²).

A unidade de pressão no Sistema Internacional (SI) é o pascal (Pa), equivalente a .

Exemplo de cálculo de pressão:

Uma força de 10 N é aplicada perpendicularmente a uma superfície de 10 cm². Qual é a pressão exercida nessa área?

Resolução:

Logo, a pressão exercida sobre a área será de 10 000 Pa.

A densidade de um fluido é a razão entre sua massa e seu volume.

Onde:

• é a densidade ou massa específica (kg/m³);
• m é a massa (kg);
• V é o volume (m³).

Exemplo de cálculo de densidade:

Uma massa de 1 kg de um fluido está contida em um recipiente com 0,8 dm³. Qual a densidade ou, massa específica deste fluido?

Resolução:

0,8 dm² = 0,0008 m³

A densidade do fluido é de 1,25 kg/m³.

A estática dos fluidos conta com três princípios fundamentais: o teorema de Stevin, o princípio de Arquimedes e o princípio de Pascal.

Princípios da Estática dos Fluidos

Teorema de Stevin: o princípio fundamental da hidrostática

O Teorema de Steviné um princípio fundamental para hidrostática e descreve como a pressão varia em um fluido em equilíbrio estático. Ele é a base para entender a relação entre a pressão, a profundidade e a densidade de um fluido.

Segundo esse princípio, a variação da pressão em um fluido homogêneo em equilíbrio depende: da profundidade, da densidade do fluido e da aceleração da gravidade. Matematicamente:

Onde:

• Δp = p2 - p1 é a diferença de pressão entre dois pontos no fluido;
• ρ é a densidade do fluido ();
• g é a aceleração da gravidade ();
• Δh é a diferença de profundidade entre os dois pontos (m).

Segundo este teorema, a pressão aumenta com a profundidade no fluido. Ainda, a variação da pressão depende apenas da profundidade, não da forma do recipiente ou da quantidade total de fluido.

A pressão total em um ponto submerso é a soma da pressão exercida pela coluna de fluido e da pressão atmosférica na superfície.

Exemplo: diferença de pressão em duas profundidades

Em uma piscina com água, qual a diferença de pressão entre 2 e 5 metros de profundidade? Utilize 1000 kg/m³ para densidade da água e 10 m/s² como aceleração da gravidade.

Resolução:

O Teorema de Stevin é fundamental para compreender e resolver problemas relacionados à pressão em fluidos e é amplamente aplicado na engenharia, na indústria e no cotidiano, como:

• Abastecimento de água
• Barômetros e medidores de pressão:.
• Sistemas de drenagem e irrigação
• Construção de barragens e diques
• Tanques industriais
• Mergulho e segurança subaquática
• Construção de piscinas
• Hidráulica em geral
• Sistemas de freios hidráulicos

Princípio de Arquimedes

Um corpo submerso total ou parcialmente em um fluido sofre uma força vertical para cima, denominada empuxo, igual ao peso do fluido deslocado. Matematicamente:

Onde:

• E é o empuxo (N);
• V é o volume do corpo submerso (m³);
• g é a aceleração da gravidade.

Este princípio explica a flutuação de objetos, sendo aplicado em projetos de barcos, submarinos e balões.

Exemplo: cálculo do empuxo.

Um brinquedo com densidade de 0,1 kg/m³ foi totalmente submerso por uma criança em uma banheira. Se o brinquedo tem um volume de 0,005 m³, qual é o valor da força empuxo sobre o brinquedo? Utilize 1000 kg/m³ para densidade da água e 10 m/s² como aceleração da gravidade.

Resolução:

Entre aplicações práticas do princípio de Arquimedes, podemos citar:

• Construção de navios e submarinos
• Balões de ar quente e dirigíveis
• Projetos de boias e flutuadores
• Construção de plataformas marítimas
• Medidores de densidade (densímetros)
• Cálculo de carga máxima em embarcações
• Testes de autenticidade de materiais
• Construção de tanques industriais

Essas aplicações destacam a importância do Princípio de Arquimedes em áreas como engenharia, ciência, transporte e até mesmo na investigação de materiais.

Princípio de Pascal

Este princípio afirma que, em um fluido confinado e em equilíbrio, qualquer variação de pressão aplicada em um ponto é transmitida integralmente para todos os pontos do fluido.

Como pressão é F/A e, as pressões são iguais em todos os pontos, suponha dois pontos de aplicação desta pressão: p1 e p2. Temos:

Logo:

Exemplo:

Em um sistema hidráulico fechado, uma força F1 = 1 N é aplicada e deve estar equilibrada com uma força F2 = 10 000 N. A área A1, de aplicação de F1, é de 0,0001 m² (1 cm²). Para que a condição de equilíbrio seja satisfeita, qual a área A2 necessária?

Resolução:

Algumas aplicações práticas do Princípio de Pascal:

• Freios hidráulicos
• Elevadores hidráulicos
• Prensas hidráulicas
• Sistemas de direção hidráulica
• Sistemas hidráulicos de aviões
• Guindastes hidráulicos
• Máquinas de injeção plástica
• Bombas hidráulicas
• Sistemas de amortecimento

Essas aplicações demonstram como o Princípio de Pascal é crucial em sistemas que requerem a transmissão e amplificação de forças em fluidos.

Mapa mental sobre estática

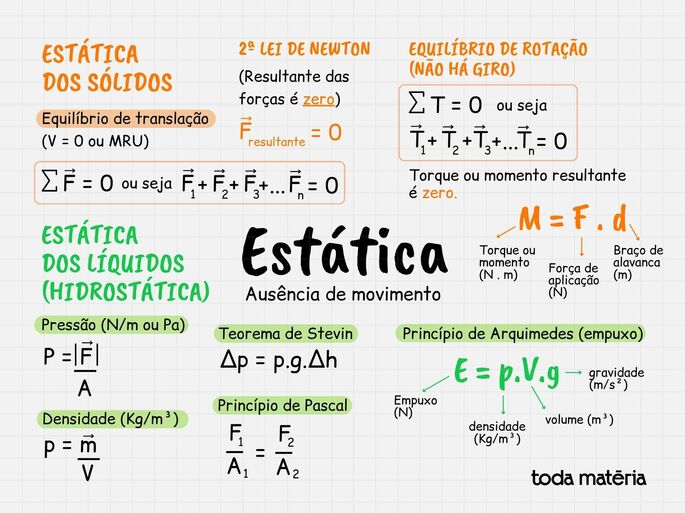
Exercícios sobre estática

Exercício 1

Veja também:

• Equilíbrio: o que é, tipos e classificação
• O que é o equilíbrio estático e dinâmico e quais suas diferenças
• Força resultante: o que é, como calcular e exercícios
• Alavanca: os tipos, como funciona e fórmula

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.