Busque um tema

Língua Portuguesa
Biologia
Matemática
História
Geografia
ENEM
Exercícios
Mais Matérias
Corretor de Redação Enem

Toda Matéria
Exercícios
›
Exercícios de Física

Exercícios de hidrostática

Rafael C. Asth

Professor de Matemática e Física

Confira abaixo 15 exercícios de hidrostática resolvidos e comentados sobre os principais conceitos dessa área: teoria hidrostática, densidade, pressão, empuxo e Lei de Stevin.

Questão 1

(UNIPAC) Uma prensa hidráulica possui pistões com diâmetros 10 cm e 20 cm. Se uma força de 120 N atua sobre o pistão menor, pode-se afirmar que esta prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de:

a) 30 N
b) 60 N
c) 480 N
d) 240 N
e) 120 N

Ver Resposta

Alternativa correta: c) 480 N.

1º passo: calcular os raios dos pistões.

O enunciado da questão apresenta o diâmetro dos pistões. Para calcular a área é necessário o raio, que corresponde ao diâmetro dividido por dois.

Raio maior:

$reto r com 1 subscrito espaço igual a espaço reto D com 1 subscrito sobre 2 reto r com 1 subscrito espaço igual a espaço numerador 20 espaço cm sobre denominador 2 fim da fração reto r com 1 subscrito espaço igual a espaço 10 espaço cm$

Raio menor:

$reto r com 2 subscrito espaço igual a espaço reto D com 2 subscrito sobre 2 reto r com 2 subscrito espaço igual a espaço numerador 10 espaço cm sobre denominador 2 fim da fração reto r com 2 subscrito espaço igual a espaço 5 espaço cm$

2º passo: calcular a área dos pistões.

Admitindo-se que área de contato é um círculo, cuja área da circunferência é dada por $reto A espaço igual a espaço πr ao quadrado$ , temos:

Área maior:

$reto A com 1 subscrito espaço igual a espaço πr ² espaço espaço reto A com 1 espaço subscrito fim do subscrito igual a espaço reto pi espaço. espaço parêntese esquerdo 10 espaço cm parêntese direito ² espaço espaço reto A com 1 subscrito espaço igual a espaço 314 vírgula 16 espaço cm ao quadrado$

Área menor:

$reto A com 2 subscrito espaço igual a espaço πr ² espaço espaço reto A com 2 subscrito espaço igual a espaço reto pi espaço. espaço parêntese esquerdo 5 espaço cm parêntese direito ² espaço espaço reto A com 2 subscrito espaço igual a espaço 78 vírgula 54 espaço cm ao quadrado$

3º passo: substituir os valores no teorema de Pascal.

$reto F com 1 subscrito sobre reto A com 1 subscrito espaço igual a espaço reto F com 2 subscrito sobre reto A com 2 subscrito reto F com 2 subscrito espaço igual a espaço espaço numerador reto A com 2 subscrito espaço reto x espaço reto F com 1 subscrito sobre denominador reto A com 1 subscrito fim da fração espaço reto F 2 espaço igual a espaço numerador 314 vírgula 16 espaço riscado diagonal para cima sobre cm ² fim do riscado espaço reto x espaço 120 espaço reto N sobre denominador 78 vírgula 54 espaço riscado diagonal para cima sobre cm ² fim do riscado fim da fração espaço reto F 2 espaço igual a espaço 480 espaço reto N$

Portanto, a prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de 480 N.

Questão 2

(UFLA) O empuxo exercido sobre um corpo imerso em um líquido depende:

a) do volume do líquido deslocado e da densidade do corpo
b) da densidade e do volume do corpo
c) do volume e da densidade do líquido deslocado
d) somente do volume do líquido deslocado
e) somente da densidade do líquido deslocado

Ver Resposta

Alternativa correta: c) do volume e da densidade do líquido deslocado.

O empuxo é uma força vertical aplicada sobre um corpo imerso, total ou parcialmente, em um fluido que está em equilíbrio, ou seja, o corpo recebe um impulso de baixo para cima.

Seu cálculo pode ser realizado utilizando a expressão E = d.g.V.

Sendo assim, o empuxo está relacionado com o volume do líquido deslocado, que corresponde ao volume da parte do corpo imersa (v), a densidade do fluido (d) e a aceleração da gravidade (g).

Questão 3

(UFV) Uma lata tampada com dois orifícios encontra-se parada, imersa em um recipiente com água. O orifício superior comunica-se com o exterior através de uma mangueira. Ao injetarmos ar pela mangueira, é correto afirmar que a lata:

a) afundará
b) subirá
c) aumentará de peso
d) permanecerá parada
e) receberá ar pelo orifício inferior

Ver Resposta

Alternativa correta: b) subirá.

A lata está imersa no recipiente com água, sendo apenas o orifício superior conectado a uma mangueira. Quando o ar começa a ser injetado dentro da lata ele desloca a quantidade de água que estava em seu inteiro, fazendo com que o líquido saia pelo outro orifício.

Como o empuxo apresenta-se na vertical e no sentido para cima, a lata subirá, pois o empuxo é diretamente proporcional ao volume de líquido deslocado.

Questão 4

(UFPEL-RS) A expressão “Isso é apenas a ponta de um iceberg” – muito usada conotativamente, hoje em dia, para mostrar que se vê apenas uma parte muito pequena de um problema, ficando o resto “escondido” – faz referência a uma situação física.

Assinale a alternativa cujos dados se relacionam corretamente com essa situação.

a) o Poder das Pontas e a Rigidez Dielétrica.
b) Arquimedes e o Teorema do Empuxo.
c) Pascal e o Princípio da Prensa Hidráulica.
d) Newton e o Princípio da Ação e Reação.
e) A Lei de Stevin e a Diferença de Pressão.

Ver Resposta

Alternativa correta: b) Arquimedes e o Teorema do Empuxo.

Os icebergs são estruturas sólidas formadas por água doce, que possuem densidade menor que a água salgada, desprendidas de geleiras polares, apresentando apenas uma parte de sua massa exposta sob a água.

O princípio de Arquimedes explica a flutuação do iceberg. Ele postulou que:

“todo corpo mergulhado num fluido recebe um impulso de baixo para cima igual ao peso do volume do fluido deslocado, por esse motivo, os corpos mais densos que a água, afundam, enquanto os menos densos flutuam”.

O empuxo é a força que sustenta os icebergs na água líquida, pois age na direção sobre o corpo imerso, mas na direção oposta à força peso.

Veja também:

Pressão Hidrostática
Teorema de Arquimedes

Questão 5

(PUC-RS) No oceano a pressão hidrostática aumenta aproximadamente uma atmosfera a cada 10 m de profundidade. Um submarino encontra-se a 200 m de profundidade, e a pressão do ar no seu interior é de uma atmosfera. Nesse contexto, pode-se concluir que a diferença da pressão entre o interior e o exterior do submarino é, aproximadamente, de

a) 200 atm
b) 100 atm
c) 21 atm
d) 20 atm
e) 19 atm

Ver Resposta

Alternativa correta: d) 20 atm.

1º passo: aplicar o teorema de Stevin para calcular a pressão externa (Pe).

$reto P com reto e subscrito espaço igual a espaço reto P com atm subscrito espaço mais espaço reto P com reto h subscrito$

Já que o enunciado diz que o submarino está a uma profundidade de 200 m e a cada 10 m a pressão hidrostática (P_h) aumenta 1 atm, então a pressão atingida é de 20 atm.

Como a pressão de ar (P_atm) no seu interior é de 1 atm, temos:

$Error converting from MathML to accessible text.$

2º passo: calcular a diferença de pressão (P_d) no interior e exterior do submarino.

Sabendo-se que a pressão interna (P_i) corresponde a 1 atm e a pressão externa (P_e) foi calculada e obtemos o resultado de 21 atm, temos:

$reto P com reto d subscrito espaço igual a espaço reto P com reto e subscrito espaço menos espaço reto P com reto i espaço subscrito fim do subscrito espaço reto P com reto d espaço subscrito fim do subscrito igual a espaço 21 espaço atm espaço menos espaço 1 espaço atm espaço espaço reto P com reto d subscrito espaço igual a espaço 20 espaço atm$

Questão 6

(UFG) Em um recipiente contendo 100 mL (1,37 kg) de mercúrio líquido, são colocados dois cubos (A e B), com volumes de 2 cm³ cada, de um material inerte diante do mercúrio. Os cubos têm massas de 14 g e 20 g, respectivamente.

Ao serem colocados no recipiente,

a) os cubos vão para o fundo.
b) o cubo A afunda e o B flutua.
c) o cubo B afunda e o A flutua.
d) os cubos flutuam a meio caminho do fundo.
e) os cubos ficam na superfície do líquido.

Ver Resposta

Alternativa correta: e) os cubos ficam na superfície do líquido.

Como o enunciado apresenta as massas e o volume dos dois cubos e do mercúrio, podemos calcular as respectivas densidades.

Densidade de A:

$reto d com reto A subscrito espaço igual a espaço reto m dividido por reto v espaço espaço reto d com reto A subscrito espaço igual a espaço 14 espaço reto g dividido por 2 espaço cm à potência de 3 espaço fim do exponencial reto d com reto A subscrito espaço igual a espaço 7 espaço reto g dividido por cm ao cubo$

Densidade de B:

$reto d com reto B subscrito espaço igual a espaço reto m dividido por reto v espaço espaço reto d com reto B subscrito espaço igual a espaço 20 espaço reto g dividido por 2 espaço cm ao cubo espaço espaço reto d com reto B subscrito espaço igual a espaço 10 espaço reto g dividido por cm ao cubo$

Densidade do mercúrio:

Sabendo que 1,37 kg = 1370 g e 100 mL = 100 cm³, temos:

$reto d com reto M subscrito espaço igual a espaço reto m dividido por reto v espaço espaço reto d com reto M subscrito espaço igual a espaço 1370 espaço reto g dividido por 100 espaço cm à potência de 3 espaço fim do exponencial espaço reto d com reto M subscrito espaço igual a espaço 13 vírgula 7 espaço reto g dividido por cm ao cubo$

Através dos dados obtidos podemos chegar a conclusão que os dados ficam na superfície do líquido, pois as densidades são menores que a do mercúrio e, portanto, eles flutuam.

Questão 7

(Enem) Um dos problemas ambientais vivenciados pela agricultura hoje em dia é a compactação do solo, devida ao intenso tráfego de máquinas cada vez mais pesadas, reduzindo a produtividade das culturas. Uma das formas de prevenir o problema de compactação do solo e substituir os pneus dos tratores por pneus mais

a) largos, reduzindo pressão sobre o solo.
b) estreitos, reduzindo a pressão sobre o solo.
c) largos, aumentando a pressão sobre o solo.
d) estreitos, aumentando a pressão sobre o solo.
e) altos, reduzindo a pressão sobre o solo.

Ver Resposta

Alternativa correta: a) largos, reduzindo pressão sobre o solo.

A pressão exercida sobre o solo é resultado da ação de uma força em determinada área. Matematicamente, a pressão pode ser calculada pela seguinte razão:

$reto P espaço igual a espaço reto F sobre reto A$

Pela fórmula, podemos perceber que a pressão (P) pode ser modificada pela quantidade de força aplicada (F) e pela área da superfície de contato (A).

Escolhendo pneus mais largos a pressão sobre o solo será diminuída, pois a área de contato é inversamente proporcional à pressão.

Portanto, quanto maior a área a força resultante do peso das máquinas será distribuída em um espaço maior, evitando a compactação do solo.

Questão 8

(UESPI) Um recipiente contendo 300 mL de água foi esquecido em um freezer por cerca de 7 horas. Após este tempo, quando a porta do freezer foi aberta, percebeu-se que

a) o volume havia aumentado devido ao aumento da densidade da água quando no estado sólido em relação à água líquida.
b) o volume havia diminuído devido à diminuição da densidade da água quando no estado sólido em relação à água líquida.
c) o volume havia diminuído devido ao aumento da densidade da água quando no estado sólido em relação à água líquida.
d) o recipiente permanecia como o mesmo volume, pois a densidade da água não aumentou nem diminuiu.
e) o volume havia aumentado devido à diminuição da densidade da água quando no estado sólido em relação à água líquida.

Ver Resposta

Alternativa correta: e) o volume havia aumentado devido à diminuição da densidade da água quando no estado sólido em relação à água líquida.

A densidade corresponde à razão da massa pelo volume de um material.

$reto d espaço igual a espaço reto m sobre reto v$

Quando resfriamos a água até o seu ponto de congelamento, sua densidade diminui fazendo com que o volume aumente, já que essas grandezas são inversamente proporcionais.

No estado líquido, as moléculas de água (H₂O) estão mais dispersas. Quando ela passa para o estado sólido as moléculas apresentam maior rigidez e as ligações de hidrogênio entre os átomos das moléculas provocam o surgimento de espaços vazios, aumentando o volume e, consequentemente, diminuindo a densidade.

Questão 9

(ACAFE-SC) - Um prego é colocado entre dois dedos, que produzem a mesma força, de modo que a ponta do prego é pressionada por um dedo e a cabeça do prego pela outra. O dedo que pressiona o lado da ponta sente dor em função de:

a) a pressão ser inversamente proporcional à área para uma mesma força.
b) a força ser diretamente proporcional à aceleração e inversamente proporcional à pressão.
c) a pressão ser diretamente proporcional à força para uma mesma área.
d) a sua área de contato ser menor e, em conseqüência, a pressão também.
e) o prego sofrer uma pressão igual em ambos os lados, mas em sentidos opostos.

Ver Resposta

Alternativa correta: a) a pressão ser inversamente proporcional à área para uma mesma força.

A pressão (P) corresponde à razão entre a força aplicada (F) e a área (A).

$reto P espaço igual a espaço reto F sobre reto A$

Note que a força é diretamente proporcional a pressão, enquanto que a área é inversamente proporcional.

Embora a mesma intensidade de força seja exercida nos dois lados do prego, as suas áreas são diferentes.

A ponta do prego possui menor área e, portanto, sentirá mais dor porque a força aplicada é direcionada a um pequeno local, enquanto que na cabeça do prego a força é melhor distribuída.

Questão 10

(UNISA) Três pessoas A, B e C de mesmo peso e altura diferentes usam: A, o mais baixo, patins para gelo; B, o de altura intermediária, patins normais com rodas e C, o mais alto, sapato de couro normal. Determine qual exerce maior pressão sobre o solo.

a) PA = PB = PC
b) PC > PB > PA
c) PA = PB > PC
d) PA > PB > PC
e) PA < PB = PC

Ver Resposta

Alternativa correta: d) PA > PB > PC.

Como as três pessoas possuem o mesmo peso, a força exercida sobre o solo será a mesma.

Entretanto, a área de contato com o solo é diferente para cada pessoa e, portanto, a pressão sobre o solo será maior quando a área de contato for a menor.

Por se tratarem de grandezas inversamente proporcionais, quanto menor a área maior a pressão.

$reto P espaço igual a espaço reto F sobre reto A$

Dessa forma, podemos organizar as pressões da maior para menor de acordo com as áreas da menor para maior, por isso PA > PB > PC.

Questão 11

(ITA) Um pedaço de gelo flutua em equilíbrio térmico com uma certa quantidade de água depositada em um balde. À medida que o gelo derrete, podemos afirmar que

a) o nível da água no balde aumenta, pois haverá uma queda de temperatura da água.
b) o nível da água no balde diminui, pois haverá uma queda de temperatura da água.
c) o nível da água no balde aumenta, pois a densidade da água é maior que a densidade do gelo.
d) o nível da água no balde diminui, pois a densidade da água é maior que a densidade do gelo.
e) o nível da água no balde não se altera.

Ver Resposta

Alternativa correta: e) o nível da água no balde não se altera.

Como o sistema está em equilíbrio, o empuxo (E) realizado pela água é igual à força peso (P) do gelo.

$reto E espaço igual a espaço reto P espaço espaço reto m com reto a subscrito espaço. espaço reto g espaço igual a espaço reto m com reto g subscrito espaço. espaço reto g reto d com reto a subscrito espaço. espaço reto V com reto i subscrito espaço. espaço reto g espaço igual a espaço reto d com reto g subscrito espaço. espaço reto V com reto g subscrito espaço. espaço reto g$

Sendo assim, o volume de gelo imerso (V_i) é calculado por:

$reto V com reto i subscrito espaço igual a espaço numerador reto d com reto g subscrito. espaço reto V com reto g subscrito espaço. espaço reto g espaço sobre denominador reto d com reto a subscrito espaço. espaço reto g fim da fração espaço reto V com reto i subscrito igual a espaço numerador reto d com reto g subscrito. espaço reto V com reto g subscrito sobre denominador reto d com reto a subscrito fim da fração espaço$

Quando o gelo derrete, ocorre a fusão e ele passa ao estado líquido e, por isso, a massa de água em estado líquido formada é igual à massa de gelo.

$reto m com reto a subscrito espaço igual a espaço reto m com reto g subscrito reto d com reto a subscrito espaço. espaço reto V com reto a subscrito espaço igual a espaço reto d com reto g subscrito espaço. espaço reto V com reto g subscrito$

Para saber o volume de água, isolamos V_a.

$reto V com reto a subscrito espaço igual a espaço numerador reto d com reto g subscrito. espaço reto V com reto g subscrito sobre denominador reto d com reto a subscrito fim da fração$

Portanto, o volume de água (V_a) corresponde ao volume de gelo imerso (V_i) e, por isso, o volume não se altera.

Questão 12

(UFRS) A atmosfera terrestre é uma imensa camada de ar, com dezenas de quilômetros de altura, que exerce uma pressão sobre os corpos nela mergulhados: a pressão atmosférica.

O físico italiano Evangelista Torricelli (1608-1647), usando um tubo de vidro com cerca de 1 m de comprimento completamente cheio de mercúrio, demonstrou que a pressão atmosférica ao nível do mar equivale à pressão exercida por uma coluna de mercúrio de 76 cm de altura. O dispositivo utilizado por Torricelli era, portanto, um tipo de barômetro, isto é, um aparelho capaz de medir a pressão atmosférica.

A esse respeito, considere as seguintes afirmações.

I – Se a experiência de Torricelli for realizada no cume de uma montanha muito alta, a altura da coluna de mercúrio será maior que ao nível do mar.

II – Se a experiência de Torricelli for realizada ao nível do mar, porém com água, cuja densidade é cerca de 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3 m.

III – Barômetros como o de Torricelli permitem, através da medida da pressão atmosférica, determinar a altitude de um lugar.

Quais estão corretas?

a) Apenas I.
b) Apenas II.
c) Apenas I e II.
d) Apenas II e III.
e) I, II e III.

Ver Resposta

Alternativa correta: d) Apenas II e III.

I. ERRADA. Na verdade, a pressão no cume de uma montanha é menor do que ao nível do mar e, por isso, a altura da coluna de mercúrio será menor.

II. CORRETA. Veja a relação entre as pressões da água (H₂O) e do mercúrio (Hg).

$reto P com Hg subscrito espaço espaço igual a espaço reto d com Hg subscrito espaço. espaço reto h com Hg subscrito espaço. espaço reto g espaço reto P com reto H com 2 subscrito reto O subscrito fim do subscrito igual a espaço reto d com reto H com 2 subscrito reto O subscrito fim do subscrito espaço. espaço reto h com reto H com 2 subscrito reto O subscrito fim do subscrito espaço. espaço reto g$

$reto P com Hg subscrito espaço igual a espaço reto P com reto H com 2 subscrito reto O espaço subscrito fim do subscrito reto d com Hg subscrito espaço. espaço reto h com Hg subscrito espaço. espaço reto g espaço igual a espaço reto d com reto H com 2 subscrito reto O subscrito fim do subscrito espaço. espaço reto h com reto H com 2 subscrito reto O espaço subscrito fim do subscrito. espaço reto g$

Sendo a densidade do mercúrio 13,6 vezes maior que a da água, temos:

$13 vírgula 6 espaço reto d com reto H com 2 subscrito reto O subscrito fim do subscrito espaço. espaço reto h com Hg subscrito espaço igual a espaço reto d com reto H com 2 subscrito reto O subscrito fim do subscrito espaço. espaço reto h com reto H com 2 subscrito reto O espaço subscrito fim do subscrito numerador 13 vírgula 6 espaço riscado diagonal para cima sobre reto d com reto H com 2 subscrito reto O subscrito fim do subscrito fim do riscado. espaço reto h com Hg subscrito sobre denominador riscado diagonal para cima sobre reto d com reto H com 2 subscrito reto O subscrito fim do subscrito fim do riscado fim da fração espaço igual a espaço reto h com reto H com 2 subscrito reto O subscrito fim do subscrito 13 vírgula 6 espaço. espaço espaço reto h com Hg subscrito espaço igual a espaço reto h com reto H com 2 subscrito reto O subscrito fim do subscrito 13 vírgula 6 espaço. espaço 0 vírgula 76 espaço reto m espaço igual a espaço reto h com reto H com 2 subscrito reto O subscrito fim do subscrito espaço reto h com reto H com 2 subscrito reto O subscrito fim do subscrito espaço igual a espaço 10 vírgula 3 espaço reto m$

III. CORRETA. Por conter uma escala no tubo de mercúrio, Torricelli obteve um aparelho capaz de medir a pressão atmosférica e também a altitude de um lugar, pois a pressão é diretamente proporcional à altura: P = d.g.h

Questão 13

(Enem) Para oferecer acessibilidade aos portadores de dificuldade de locomoção, é utilizado, em ônibus e automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a plataforma. Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba. Desprezando o atrito e considerando uma aceleração gravitacional de 10 m/s², deseja-se elevar uma pessoa de 65 kg em uma cadeira de rodas de 15 kg sobre a plataforma de 20 kg.

Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante?

a) 20 N
b) 100 N
c) 200 N
d) 1000 N
e) 5000 N

Ver Resposta

Alternativa correta: c) 200 N.

Para resolver essa questão, utilizaremos a fórmula da Lei de Pascal.

$ΔP com reto A subscrito espaço igual a espaço ΔP com reto B subscrito$

A pressão pode ser representada através da razão da força pela área.

$reto f sobre reto A com 1 subscrito espaço igual a espaço numerador reto F espaço sobre denominador reto A com 2 subscrito fim da fração reto f espaço igual a espaço reto F espaço. espaço reto A com 1 subscrito sobre reto A com 2 subscrito$

Como a área da cabeça do pistão (A₂) é cinco vezes maior que a área da tubulação que sai da bomba (A₁), podemos transformar a fórmula em

$reto f espaço igual a espaço reto F espaço. espaço numerador riscado diagonal para cima sobre reto A 1 fim do riscado sobre denominador 5 riscado diagonal para cima sobre reto A 1 fim do riscado fim da fração espaço espaço reto f espaço igual a espaço reto F sobre 5$

Agora, com os dados do enunciado, calculamos o valor de F.

$reto F espaço igual a espaço reto P com total espaço subscrito fim do subscrito igual a espaço reto m espaço. espaço reto g reto F espaço igual a espaço parêntese esquerdo reto m com pessoa subscrito espaço mais espaço reto m com cadeira subscrito espaço mais espaço reto m com plataforma subscrito parêntese direito espaço. espaço reto g espaço reto F espaço igual a espaço parêntese esquerdo 65 espaço kg mais espaço 15 espaço kg espaço mais espaço 20 espaço kg parêntese direito espaço. espaço 10 espaço reto m dividido por reto s ao quadrado espaço reto F espaço igual a espaço 100 espaço kg espaço. espaço 10 espaço reto m dividido por reto s ao quadrado espaço reto F espaço igual a espaço 1000 espaço numerador kg espaço. espaço reto m sobre denominador reto s ao quadrado fim da fração reto F igual a espaço 1000 espaço reto N$

Com o valor encontrado, podemos calcular a força exercida pelo motor da bomba.

$reto f espaço igual a espaço reto F sobre 5 reto f espaço igual a espaço numerador 1000 espaço reto N sobre denominador 5 fim da fração reto f espaço igual a espaço 200 espaço reto N$

Portanto, a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante é de 200 N.

Questão 14

(Enem) Um tipo de vaso sanitário que vem substituindo as válvulas de descarga está esquematizado na figura. Ao acionar a alavanca, toda a água do tanque é escoada e aumenta o nível no vaso, até cobrir o sifão. De acordo com o Teorema de Stevin, quanto maior a profundidade, maior a pressão. Assim, a água desce levando os rejeitos até o sistema de esgoto. A válvula da caixa de descarga se fecha e ocorre o seu enchimento. Em relação às válvulas de descarga, esse tipo de sistema proporciona maior economia de água.

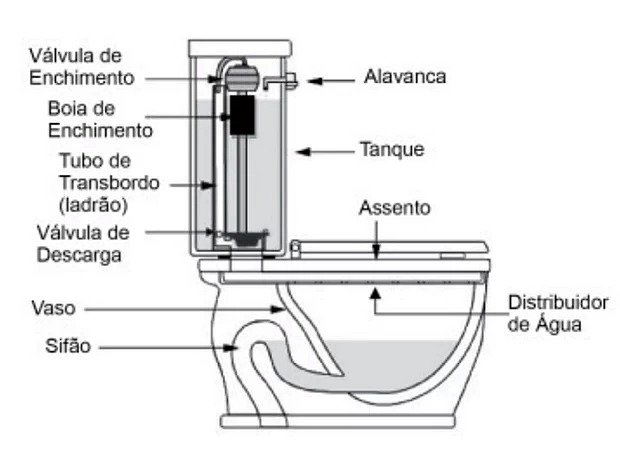
^{Faça você mesmo. Disponível em: http://www.facavocemesmo.net. Acesso em: 22 jul. 2010. (Foto: Reprodução/Enem)}

A característica de funcionamento que garante essa economia é devida

a) à altura do sifão de água.
b) ao volume do tanque de água.
c) à altura do nível de água no vaso.
d) ao diâmetro do distribuidor de água.
e) à eficiência da válvula de enchimento do tanque.

Ver Resposta

Alternativa correta: b) ao volume do tanque de água.

O Teorema de Stevin citado no enunciado faz a seguinte relação matemática:

$reto P com hid subscrito igual a µ. reto g. reto h$

Onde,

P_hid é a pressão hidrostática
µ é a massa específica do fluido
g é a força da gravidade
h é a altura do fluido

Vemos que a pressão hidrostática é proporcional à altura do fluido, que no enunciado é a água. Portanto, garante-se a economia pelo volume no tanque devido à pressão exercida pela coluna de água.

Questão 15

(UFPR) Um reservatório cilíndrico de 2 m de altura e base com área 2,4 m², como mostra a figura, foi escolhido para guardar um produto líquido de massa específica igual a 1,2 g/cm³. Durante o enchimento, quando o líquido atingiu a altura de 1,8 m em relação ao fundo do reservatório, este não suportou a pressão do líquido e se rompeu. Com base nesses dados, assinale a alternativa correta para o módulo da força máxima suportada pelo fundo do reservatório.

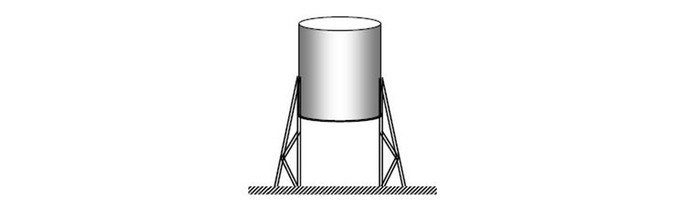
a) É maior que 58.000 N.
b) É menor que 49.000 N.
c) É igual a 50.000 N.
d) Está entre 50.100 N e 52.000 N.
e) Está entre 49.100 N e 49.800 N.

Ver Resposta

Alternativa correta: d) Está entre 50.100 N e 52.000 N.

Dados do enunciado são:

h_c = 2 m
A_bc = 2,4 m²
µ_L = 1,2 g/cm³
h_L = 1,8 m

1º passo: calcular o volume de líquido no cilindro utilizado como reservatório:

$reto V espaço igual a espaço reto pi. reto r ². reto h espaço reto V espaço igual a espaço reto A com reto b subscrito espaço. espaço reto h reto V espaço igual a espaço 2 vírgula 4 espaço reto m ao quadrado espaço. espaço 1 vírgula 8 espaço reto m espaço reto V espaço igual a espaço 4 vírgula 32 espaço reto m ao cubo$

2º passo: encontrar a massa de líquido que corresponde ao volume de 4,32 m³.

Sabendo que 4,32 m³ equivale a 4,32 . 10⁶ cm³, temos:

$reto mu espaço igual a espaço reto m sobre reto V espaço 1 vírgula 2 espaço reto g dividido por cm à potência de 3 espaço fim do exponencial igual a espaço numerador reto m sobre denominador espaço 4 vírgula 32.10 à potência de 6 espaço cm ao cubo espaço fim da fração reto m espaço igual a espaço 1 vírgula 2 espaço reto g dividido por cm à potência de 3 espaço fim do exponencial. espaço 4 vírgula 32.10 à potência de 6 espaço cm ao cubo espaço reto m espaço igual a espaço 5 vírgula 184.10 à potência de 6 espaço reto g$

3º passo: converter a unidade de massa de g para kg.

$tabela linha com célula com 1000 espaço reto g espaço fim da célula menos célula com 1 espaço kg espaço fim da célula linha com célula com 5 vírgula 184.10 à potência de 6 espaço reto g fim da célula menos célula com reto x espaço espaço fim da célula fim da tabela reto x espaço igual a espaço numerador 5 vírgula 184.10 à potência de 6 espaço diagonal para cima risco reto g espaço. espaço 1 espaço kg sobre denominador 1000 espaço diagonal para cima risco reto g fim da fração reto x espaço igual a espaço 5184 espaço kg$

4º passo: calcular a força peso exercida pelo líquido.

$reto P espaço igual a espaço reto m espaço. espaço reto a espaço reto P espaço igual a espaço 5184 espaço kg espaço. espaço 10 espaço reto m dividido por reto s ao quadrado espaço reto P espaço igual a espaço 51840 espaço numerador kg espaço. espaço reto m sobre denominador reto s ao quadrado fim da fração reto P espaço igual a espaço 51840 espaço reto N$

Portanto, a força de 51840 N está entre 50.100 N e 52.000 N, conforme a alternativa d.

Questão 16

(Enem 2021) As moedas despertam o interesse de colecionadores, numismatas e investidores há bastante tempo. Uma moeda de 100% cobre, circulante no período do Brasil Colônia, pode ser bastante valiosa. O elevado valor gera a necessidade de realização de testes que validem a procedência da moeda, bem como a veracidade de sua composição. Sabendo que a densidade do cobre metálico é próxima de 9 g cm-3, um investidor negocia a aquisição de um lote de quatro moedas A, B, C e D fabricadas supostamente de 100% cobre e massas 26 g, 27 g, 10 g e 36 g, respectivamente. Com o objetivo de testar a densidade das moedas, foi realizado um procedimento em que elas foram sequencialmente inseridas em uma proveta contendo 5 mL de água, conforme esquematizado.

Com base nos dados obtidos, o investidor adquiriu as moedas

a) A e B.
b) A e C.
c) B e C.
d) B e D.
e) C e D.

Ver Resposta

Resposta correta: d) B e D.

Dados
Densidade do cobre: $9 espaço numerador g sobre denominador c m ao cubo fim da fração igual a 9 espaço g. c m à potência de menos 3 fim do exponencial$

Massas das moedas
A = 26 g
B = 27 g
C = 10 g
D = 36 g

Proveta com 5 ml de água.

Objetivo
Verificar se as moedas são feitas 100% de cobre.

Resolução
A densidade de um material ou elemento é obtida pela razão entre a massa e o volume.

$reto ró espaço igual a espaço reto m sobre reto V$

Onde,
$ró$ é a densidade;
m é a massa;
V é o volume.

Como já possuímos as massas das moedas, precisamos determinar seu volume. Essa informação é obtida na imagem do experimento.

O volume de cada moeda é igual ao volume de líquido deslocado. Após identificar o volume deslocado, é preciso transformar a unidade de capacidade ml, em unidade de volume, o cm³. Como essa relação é de 1 para 1, temos:

$1 espaço m l espaço igual a espaço 1 espaço c m ao cubo$

Moeda A
Após inserir a moeda na proveta, o volume de água aumentou 2 ml, pelo que observamos na escala à esquerda. Assim, o volume da moeda A é de 2 cm³.

Moeda B
Após ter inserido a moeda A, o nível na proveta marca 7 ml, inserindo a moeda B, vai para 10 ml, um aumento de 3 ml. Assim, o volume da moeda B é de 3 cm³.

Moeda C
Após inserir a moeda C, o nível da água se eleva 2 ml. Assim, o volume da moeda C é de 2 cm³.

Moeda D
Após inserir a moeda D, o nível da água se eleva 4 ml. Assim, o volume da moeda D é de 4 cm³.

Calculo das densidades
Moeda A: não é de cobre puro.

$ró com A subscrito igual a m com A subscrito sobre V com A subscrito igual a 26 sobre 2 igual a 13 espaço g dividido por c m ao cubo$

Moeda B: é de cobre puro.

$ró com B subscrito igual a m com B subscrito sobre V com B subscrito igual a 27 sobre 3 igual a 9 espaço g dividido por c m ao cubo$

Moeda C: Não é de cobre puro.

$ró com C subscrito igual a m com C subscrito sobre V com C subscrito igual a 10 sobre 2 igual a 5 espaço g dividido por c m ao cubo$

Moeda D: é de cobre puro.

$ró com D subscrito igual a m com D subscrito sobre V com D subscrito igual a 36 sobre 4 igual a 9 espaço g dividido por c m ao cubo$

Conclusão
O investidor adquiriu as moedas B e D que são de cobre puro, uma vez que suas densidades são igual à densidade do cobre.

Questão 17

(CEDERJ 2020) De acordo com o Princípio de Arquimedes, "Quando um corpo está totalmente submerso, ou mesmo parcialmente submerso, em um fluido (líquido ou gás) em equilíbrio, este exerce sobre o corpo uma força vertical E, denominada empuxo, cujo sentido é para cima, isto é, oposto ao sentido do peso p" do corpo”.
As figuras 1, 2, 3 e 4 representam quatro situações nas quais quatro esferas estão totalmente ou parcialmente submersas em um tanque que contém água. Apesar de serem constituídas de materiais diferentes umas das outras, todas as esferas possuem o mesmo volume V. Sabe-se que, nas figuras 2 e 3, as esferas têm metade do seu volume submerso (V/2).

Ao se comparar os módulos dos empuxos E1, E2, E3, E4, que se referem respectivamente às forças que a água exerce sobre as esferas nas situações representadas nas figuras 1, 2, 3, e 4,é correto afirmar que:

a) E1 = E2 = E3 = E4

b) E1 > E2 > E3 >E4

c) E1 > E4 > E2 = E3

d) E1 = E4 > E2 = E3

Veja exercícios sobre densidade.

Ver Resposta

Resposta: d) E1 = E4 > E2 = E3

O empuxo depende apenas da densidade do fluido, da aceleração da gravidade e do volume de fluida deslocado.

$reto E igual a reto d com reto f subscrito espaço. espaço reto g espaço. espaço reto V com reto f subscrito$

Como os fluidos são iguais e a aceleração da gravidade também, a comparação depende apenas do volume de fluido deslocado.

Dessa forma E1 = E4, pois, as duas esferas estão totalmente submersas e possuem o mesmo volume.

Também temos que, E2 = E3, pois as duas esferas possuem o mesmo volume e estão com a metade submersa.

Ainda, os empuxos em 1 e 4 são maiores que em 2 e 3, pois os volumes em 2 e 3 são apenas a metade das esferas totalmente submersas.

Conclusão
E1 = E4 > E2 = E3

Questão 18

(Marinha 2021) Há uma regra prática utilizada pelos Mergulhadores da Marinha que diz que a cada 10m de profundidade na água a pressão aumenta em uma atmosfera. Um Suboficial Mergulhador (SO-MG) com bastante experiência na profissão realiza um mergulho no fundo do mar a 40m' de profundidade. Determine a pressão total sobre o fundo do mar e marque a opção correta: :

a) 4atm
b) 5atm
c) 6atm
d) 7atm
e) 8atm

Ver Resposta

Resposta: b) 5atm

Se a cada 10 m abaixo da superfície a regra prática diz que a pressão aumenta em 1 atm, se o mergulhador descer 40 m, teremos a pressão de 4 atm, mais 1 atmosfera acima do nível da água, sendo 5 ao total.

Veja mais exercícios de Física (resolvidos) para 1º ano do ensino médio.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

ASTH, Rafael. Exercícios de hidrostática. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-hidrostatica/. Acesso em:

Veja também