Exercícios sobre energia mecânica (com gabarito explicado)
O tema energia mecânica é visto frequentemente nos vestibulares e também no colégio.
Faça estes exercícios com respostas explicadas para treinar suas habilidades e aprofundar seu conhecimento sobre este conceito da Física.
Questão 1
Um ciclista de 70 kg está descendo uma colina inclinada de 20 metros de altura. No topo da colina, ele está parado, ou seja, sua velocidade inicial é zero. Ao chegar na base da colina, o ciclista atinge uma velocidade de 14 m/s.
Considerando não haver perda de energia por atrito ou resistência do ar, qual é a forma de energia que prevalece na base da colina e o que aconteceu com a energia ao longo do percurso?
a) A energia mecânica total diminuiu, e a energia cinética foi transformada em energia potencial gravitacional.
b) A energia mecânica total permaneceu constante, com a energia potencial sendo completamente transformada em energia cinética na base da colina.
c) A energia cinética na base da colina é maior do que a energia potencial no topo, indicando um ganho de energia mecânica ao longo do caminho.s.
d) A energia potencial no topo da colina foi completamente transformada em energia térmica e sonora ao longo do caminho.
e) A energia potencial e a energia cinética se mantêm constantes durante todo o percurso, já que não há forças dissipativas.
Dados:
- Massa do ciclista: 70 kg
- Altura da colina: 20 metros
- Velocidade na base: 14 m/s
- Aceleração da gravidade: 10 m/s²
Para resolver esse problema, devemos entender o princípio da conservação da energia mecânica.
Em sistemas onde não há perda de energia por atrito ou resistência do ar, a energia mecânica total (soma da energia potencial gravitacional e da energia cinética) permanece constante ao longo do movimento.
Passo 1: energia potencial gravitacional no topo da colina.
Onde:
- Massa do ciclista: 70 kg
- Aceleração da gravidade: 10 m/s²
- Altura da colina: 20 metros
Substituindo os valores:
Portanto, a energia potencial no topo da colina é 14.000 J.
Passo 2: energia cinética na base da colina.
Onde:
- Massa do ciclista: 70 kg
- Velocidade na base: 14 m/s
Substituindo na equação:
Interpretação:
No topo da colina, o ciclista tinha energia potencial gravitacional máxima.
Na base da colina, essa energia potencial foi convertida em energia cinética.
Como não há forças dissipativas, a energia mecânica total (potencial + cinética) permaneceu constante.
Logo, a energia potencial no topo foi completamente transformada em energia cinética na base.
Questão 2
Um garoto de 40 kg está no topo de um escorregador com uma altura de 10 metros. Inicialmente, ele está parado, e ao descer, não há perda de energia por atrito ou resistência do ar. Considerando que toda a energia potencial gravitacional é convertida em energia cinética, qual será a velocidade do garoto ao chegar ao ponto mais baixo do escorregador?
a) 5 m/s
b) 10 m/s
c) 14 m/s
d) 20 m/s
e) 28 m/s
Dados:
- Massa do garoto: 40 kg
- Altura do escorregador: 10 metros
- Aceleração da gravidade: 10 m/s²
Apliquemos a lei da conservação da energia mecânica para resolver o problema. De acordo com essa lei, a energia mecânica total (energia potencial + energia cinética) se conserva se não houver dissipação de energia. Ou seja, a energia potencial gravitacional no topo será totalmente convertida em energia cinética no final do escorregador.
Passo 1: energia potencial gravitacional no topo do escorregador.
Substituindo os valores fornecidos:
Passo 2: energia cinética no ponto mais baixo.
Substituindo os valores e resolvendo para determinar v:
Assim, a velocidade no ponto mais baixo da trajetória será de aproximadamente 14 m/s.
Questão 3
Considere as seguintes afirmações a respeito da energia mecânica:
I. A energia mecânica de um sistema é a soma da energia cinética e da energia potencial do sistema.
II. Em um sistema conservativo, sem a presença de forças dissipativas como o atrito, a energia mecânica total se mantém constante.
III. A energia cinética de um objeto depende exclusivamente da sua altura em relação ao solo.
IV. Quando um corpo em movimento atinge a altura máxima, toda a sua energia cinética é convertida em energia potencial gravitacional, assumindo não haver resistência do ar.
Quais afirmações são verdadeiras?
a) Apenas I e II
b) Apenas II e IV
c) Apenas I, II e IV
d) Apenas I e IV
e) Todas as afirmativas estão corretas
Afirmação I - Verdadeira: A energia mecânica é, de fato, a soma da energia cinética e da energia potencial. Essa definição é fundamental em física.
Afirmação II - Verdadeira: Em um sistema onde não há forças dissipativas (como o atrito), a energia mecânica total é conservada, ou seja, permanece constante durante o movimento.
Afirmação III - Falsa: A energia cinética de um objeto depende de sua massa e velocidade, e não da altura. A altura influencia a energia potencial gravitacional, não a cinética.
Afirmação IV - Verdadeira: Quando um corpo atinge a altura máxima em um movimento (como em um lançamento vertical), toda a energia cinética é convertida em energia potencial gravitacional, desde que não haja resistência do ar ou outras forças dissipativas.
Portanto, as afirmações I, II e IV estão corretas, enquanto a afirmação III está errada.
Questão 4
Um ciclista desce uma ladeira íngreme sem pedalar. No topo da ladeira, ele possui apenas energia potencial gravitacional, e à medida que desce, essa energia se converte em energia cinética, sem perda de energia para o atrito ou o ar. Considere as seguintes afirmações sobre a situação descrita:
I. No ponto mais baixo da ladeira, toda a energia potencial gravitacional foi convertida em energia cinética.
II. Durante a descida, a soma da energia cinética e da energia potencial gravitacional permanece constante.
III. A energia potencial gravitacional é máxima no ponto mais baixo da ladeira.
IV. A energia cinética do ciclista no meio da ladeira é menor do que no ponto mais baixo, mas maior do que no topo.
Quais afirmações são verdadeiras?
a) Apenas I e II
b) Apenas II e IV
c) Apenas I, II e IV
d) Apenas II e III
e) Todas as afirmativas estão corretas
Afirmação I - Verdadeira: No ponto mais baixo da ladeira, toda a energia potencial gravitacional do ciclista foi convertida em energia cinética, pois ele está na menor altura possível e com sua velocidade máxima.
Afirmação II - Verdadeira: Durante a descida, se não há atrito ou resistência do ar, a soma da energia potencial e da energia cinética permanece constante, conforme a lei de conservação da energia mecânica.
Afirmação III - Falsa: No ponto mais baixo da ladeira, a energia potencial gravitacional é mínima, não máxima, pois a altura em relação ao solo é zero nesse ponto.
Afirmação IV - Verdadeira: No meio da ladeira, o ciclista ainda possui parte de sua energia potencial, que foi parcialmente convertida em energia cinética. Portanto, sua energia cinética no meio da descida é maior do que no topo, mas menor do que no ponto mais baixo.
As afirmações I, II e IV estão corretas, enquanto a afirmação III está errada.
Questão 5
Um bloco de massa 2 kg está preso a uma mola horizontal com constante elástica k=100 N/m em uma superfície sem atrito. A mola está comprimida em 0,5 m em relação à sua posição de equilíbrio. Quando o bloco é solto, ele se move e a mola se distende até sua posição natural (de equilíbrio), sem que haja perda de energia.
Qual será a velocidade aproximadada bloco no momento em que a mola atinge a posição de equilíbrio, ou seja, quando a mola não está nem comprimida nem esticada?
a) 1 m/s
b) 3,5 m/s
c) 5,0 m/s
d) 10,5 m/s
e) 15,0 m/s
Dados:
- Massa do bloco: m=2 kg;
- Constante elástica da mola: k=100 N/m;
- Compressão inicial da mola: x=0,5 m;
- Superfície sem atrito
A conservação da energia mecânica nos diz que a energia potencial elástica armazenada na mola quando ela está comprimida será completamente convertida em energia cinética no momento em que a mola atingir sua posição de equilíbrio.
A energia potencial elástica armazenada na mola é dada pela fórmula:
Onde:
- k é constante elástica da mola;
- x é a deformação da mola.
Substituindo os valores:
No ponto de equilíbrio da mola, toda essa energia será convertida em energia cinética do bloco:
Igualando a energia potencial elástica à energia cinética, temos:
Questão 6
(Enem 2018) Um projetista deseja construir um brinquedo que lance um pequeno cubo ao longo de um trilho horizontal, e o dispositivo precisa oferecer a opção de mudar a velocidade de lançamento. Para isso, ele utiliza uma mola e um trilho onde o atrito pode ser desprezado, conforme a figura.
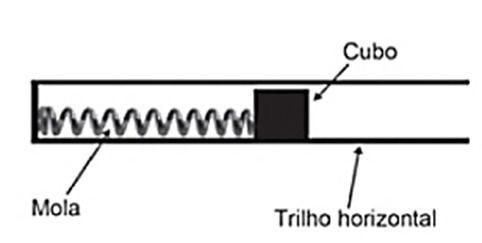
Para que a velocidade de lançamento do cubo seja aumentada quatro vezes, o projetista deve
A) manter a mesma mola e aumentar duas vezes a sua deformação.
B) manter a mesma mola e aumentar quatro vezes a sua deformação.
C) manter a mesma mola e aumentar dezesseis vezes a sua deformação.
D) trocar a mola por outra de constante elástica duas vezes maior e manter a deformação.
E) trocar a mola por outra de constante elástica quatro vezes maior e manter a deformação.
Como o atrito é desprezado, consideraremos o sistema como conservativo. Assim, toda energia potencial elástica será convertida em energia cinética.
A fórmula para calcular a energia potencial elástica é:
Onde:
- Epe é a energia potencial elástica, em J (joules);
- k é a constante elástica da mola, em N/m;
- x é a deformação da mola, em metros.
A fórmula para calcular a energia cinética é:
Onde:
- m é a massa em quilogramas;
- v é a velocidade em m/s.
Como a potencial elástica se converte integralmente em energia cinética, igualamos as fórmulas:
Isolando o v:
Assim, para aumentar a velocidade quatro vezes, devemos aumentar a deformação (x) quatro vezes.
Questão 7
(Enem 2020) Usando pressões extremamente altas, equivalentes às encontradas nas profundezas da Terra ou em um planeta gigante, cientistas criaram um novo cristal capaz de armazenar quantidades enormes de energia. Utilizando-se um aparato chamado bigorna de diamante, um cristal de difluoreto de xenônio (XeF2) foi pressionado, gerando um novo cristal com estrutura supercompacta e enorme quantidade de energia acumulada.
Inovação Tecnológica. Disponível em: http://www.inovacaotecnologica.com.br. Acesso em: 07 jul. 2010 (adaptado).
Embora as condições citadas sejam diferentes do cotidiano, o processo de acumulação de energia descrito é análogo ao da energia
A) armazenada em um carrinho de montanha russa durante o trajeto.
B) armazenada na água do reservatório de uma usina hidrelétrica.
C) liberada na queima de um palito de fósforo.
D) gerada nos reatores das usinas nucleares.
E) acumulada em uma mola comprimida.
O processo descrito no enunciado envolve a criação de um cristal de difluoreto de xenônio (XeF2) que foi comprimido, armazenando uma enorme quantidade de energia devido à sua nova estrutura supercompacta.
Esse processo é análogo ao armazenamento de energia em uma mola comprimida, que também acumula energia potencial elástica quando submetida a uma força externa de compressão.
A energia armazenada em uma mola comprimida é um exemplo clássico de energia potencial elástica, liberada quando a mola retorna à sua forma original.
As outras opções, como a energia em uma montanha-russa ou em uma usina hidrelétrica, estão relacionadas a energia potencial gravitacional.
A queima de um palito de fósforo refere-se a uma reação química, liberando energia térmica.
A geração de energia em usinas nucleares envolve energia nuclear, liberada pela fissão dos núcleos de átomos.
Portanto, a analogia mais precisa com o processo descrito no enunciado é a compressão de uma mola, que armazena energia de forma elástica.
Questão 8
Aprenda mais sobre energia com:
- Energia Mecânica
- Energia Cinética: definição, fórmulas e exercícios
- Energia Potencial
- Energia Potencial Gravitacional
- Energia Potencial Elástica
Para mais exercícios:
Referências Bibliográficas
Resnick, R., Halliday, D., & Walker, J. (2008). Fundamentos de Física (Vol. 1). Rio de Janeiro: LTC.
ASTH, Rafael. Exercícios sobre energia mecânica (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-energia-mecanica/. Acesso em:


