Exercícios sobre óptica geométrica (com respostas explicadas)

I. Falsa: Na situação A, o tamanho da imagem é de 5,0 cm, o que não significa que a altura do prédio seja igual à metade da distância. A relação entre o tamanho da imagem e a distância focal de uma câmara escura é dada pela equação dos semelhantes, e a altura do prédio não é diretamente determinada apenas pela metade da distância.

II. Verdadeira: Como na situação B a distância entre o estudante e a câmara aumentou, o tamanho da imagem diminuiu (4,0 cm), o que sugere que a altura percebida do prédio também diminuiu. Portanto, a altura do prédio na situação B é menor do que na situação A.

III. Verdadeira: Ao se afastar do edifício, o estudante diminuiu a distância entre o prédio e a câmara escura, o que resultou em uma imagem maior na situação A. Ao comparar as situações A e B, onde houve um aumento de 10 m na distância entre a câmara e o edifício, e a imagem do prédio diminuiu de 5,0 cm para 4,0 cm, podemos concluir que a altura real do prédio é maior do que 20 m.

A reflexão da luz é o fenômeno que ocorre quando a luz incide sobre uma superfície e retorna para o meio em que estava se propagando. Isso acontece porque a luz não consegue penetrar completamente em certos materiais e é refletida de volta ao entrar em contato com a superfície.

Para calcular o intervalo de tempo decorrido desde a emissão de um pulso luminoso no Sol até sua recepção na Terra, podemos usar a fórmula da velocidade:

Logo,

Dado que a distância do Sol à Terra é de aproximadamente 150 000 000 km e a velocidade da luz no vácuo é de 300 000 000 m/s, podemos substituir esses valores na fórmula e calcular.

Transformando distância em Km para m.

150 000 000 km = 150 000 000 x 1000 m = 150 000 000 000 m

ou

Escrevendo a velocidade da luz utilizando notação científica:

Realizando o cálculo:

Transformando em minutos.

60 s x 8 = 480 s

500 - 480 = 20 s

Assim, são 8 min mais 20 s para a luz chegar à Terra.

Podemos fazer um esboço representativo da imagem.

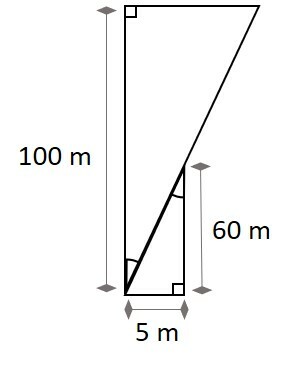
No esboço acima, consideramos apenas a metada da rua, ou seja, 5 metros. Representamos também a altura em que o helicópero se encontra, assim como, a altura de 60 m dos prédios.

Podemos considerar este modelo geométrico pois conhecemos o comportamento dos raios de luz, que sempre se movem em linhas retas.

A luz que reflete no helicóptero viaja até os olhos do observador no solo, tangenciando os prédios.

Esta formação produz um par de triângulos semelhes, onde podemos formar uma proporção entre seus lados.

Chamando de x essa metade da medida do helicóptero e resolvendo a regra de três:

Importa lembrar que x é apenas metade da medida procurada, devendo ser multiplicada por 2.

Assim, o comprimento do helicópero é de, aproximadamente, 16,66 m.

Para resolver este exercício, podemos usar a Lei de Snell-Descartes, que relaciona os ângulos de incidência e refração com os índices de refração dos meios envolvidos. A lei é dada pela seguinte equação:

Onde:

n1 e n2 são os índices de refração dos meios inicial e final, respectivamente.

i é o ângulo de incidência.

r é o ângulo de refração.

Neste caso, temo:

n1 = 1

n2 = 1,33

i = 30º

O seno do ângulo de 30° é igual a 1/2.

Substituindo os valores conhecidos na equação da Lei de Snell-Descartes, temos:

Agora, precisamos encontrar o ângulo cujo seno é aproximadamente 0,37.

Usando a função inversa do seno (arcseno), podemos encontrar o ângulo:

Portanto, o ângulo de refração do raio de luz ao entrar na água é de aproximadamente 21,7º.

Para resolver a questão, utilizamos a equação dos espelhos esféricos, dada por:

Onde,

• é a distância do objeto ao espelho;
• é a distância da imagem ao espelho.
• f é a distância focal.

Substituindo os valores fornecidos:

Calculando para :

O número de imagens formadas pela associação de espelhos planos depende do ângulo entre eles e, é dado pela fórmula:

Sendo n um número ímpar.

Na questão, n = 5. Assim, o ângulo entre os espelhos será:

Distancia focal "f" é o comprimento entre o vértice e o foco principal. Ela se relaciona com o raio "R" do espelho pela fórmula:

Como f = 0,1 m, temos:

R = 2 . 0,1 = 0,2 m

ou 20 cm.

Os raios paralelos ao eixo principal de um espelho côncavo convergem para um ponto focal real. Esta afirmação é verdadeira. De acordo com as leis da reflexão, raios paralelos ao eixo principal de um espelho côncavo são refletidos de tal forma que se convergem para um ponto focal real.

Os raios que passam pelo centro de curvatura do espelho côncavo são refletidos de volta na mesma direção. Esta afirmação é verdadeira. Quando um raio de luz incide perpendicularmente à superfície de um espelho, ele é refletido de volta na mesma direção, seguindo a lei da reflexão.

Os raios que incidem perpendicularmente à superfície do espelho côncavo são refletidos de volta na mesma direção. Esta afirmação é falsa. Quando um raio de luz incide perpendicularmente à superfície de um espelho, ele é refletido de volta na mesma direção, mas não necessariamente seguindo a direção original. A direção exata do raio refletido depende da forma do espelho e da posição do ponto de incidência.

Portanto, as afirmações 1 e 2 são verdadeiras, enquanto a afirmação 3 é falsa.

As características da imagem formada dependem da posição do objeto ao longo do eixo principal e sua posição em relação ao vértice, foco e centro de curvatura.

Objeto Entre o Foco (F) e o Vértice (V)

• Posição da Imagem: Atrás do espelho.
• Tipo de Imagem: Virtual e direita.
• Tamanho da Imagem: Maior que o objeto.