Exercícios sobre refração da luz (com respostas explicadas)
Pratique seus conhecimentos sobre a refração da luz e tire suas dúvidas com o gabarito comentado.
Questão 1
Em um estudo de óptica sobre a refração da luz é realizado um experimento em que um raio de luz passa de um meio para outro, resultando em mudança na sua direção.
Se o segundo meio tem um índice de refração maior que o primeiro, assim, a trajetória do raio de luz irá
a) se aproximar da reta normal.
b) se afastar da reta normal.
c) permanecer com mesma trajetória.
d) ocorrer reflexão total.
e) se desviar do plano incidente.
Quando um raio de luz passa de um meio para outro com um índice de refração maior, ele se aproxima da reta normal.
Isso ocorre devido à mudança na velocidade da luz nos diferentes meios, conforme descrito pela lei de Snell. A aproximação da reta normal é uma consequência dos casos de refração onde o índice de refração do segundo meio é maior que o do primeiro.
Questão 2
A imagem abaixo constitue um esquema em que um raio de luz no meio 1 atinge uma superfície que separa do meio 2, com maior índice de refração. Uma porção da energia luminosa é refletida e outra refratada. Ainda há as identificações: A, B, C, D e E.
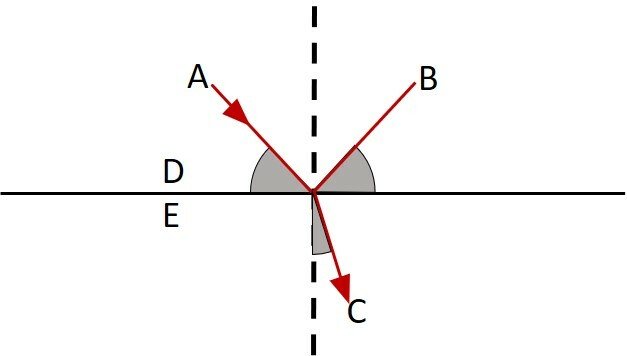
A opção que relaciona corretamente os identificadores com os elementos da figura é:
a) A é o raio incidente, B é o raio refletido, C é o meio 2, D é o meio 1 e E o meio 2.
b) C) A é o raio refratado, B é o raio incidente, C é o raio incidente, D é o meio 1 e E o meio 2.
C) A é o raio refletido, B é o raio incidente, C é o raio refratado, D é o meio 1 e E o meio 2.
d) A é o raio incidente, B é o raio refletido, C é o raio refratado, D é o meio 1 e E o meio 2.
C) A é o raio refletido, B é o raio incidente, C é o raio refletido, D é o meio 2 e E o meio 1.
Como o meio 2 possui maior índice de refração, ao passar do meio 1 para o 2, o raio se aproxima da reta normal. Assim, A é o raio incidente, e C o refratado, sobrando apenas o B como raio refletido.
Questão 3
Um feixe de luz está se propagando no ar e incide em uma placa de acrílico com um ângulo de 45° em relação à normal. Se o índice de refração do ar é 1,0 e o índice de refração do acrílico é 1,4, qual será o ângulo de refração do raio de luz ao entrar no acrílico?
a) 20°
b) 30°
c) 45°
d) 50°
e) 60°
Para encontrar o ângulo de refração θ2, usamos a Lei de Snell, dada pela fórmula:
Onde:
n1 = índice de refração do meio incidente (ar) = 1,0
n2 = índice de refração do meio refrativo (acrílico) = 1,4
θ1 = ângulo de incidência = 45°
θ2 = ângulo de refração (a ser encontrado)
Substituindo os valores conhecidos, temos:
Aproximando a raiz quadrada:
O ângulo cujo seno vale 1/2 é de 30º.
Portanto, a resposta correta é b) 30°.
Questão 4
Um feixe de luz está se propagando no ar e incide em outro meio, com um ângulo de 30° em relação à normal. Se o ângulo de refração ao entrar no segundo meio é de 20°, qual é o índice de refração da água?
Considere para este exercício:
sin 30º = 0,5 e sin 20º = 0,34
e 
a) 
b) 
c) 
d) 
e) 2
Usaremos a Lei de Snell para encontrar o índice de refração da água. A fórmula da Lei de Snell é dada por:
Onde:
n1 = índice de refração do meio incidente (ar) = 1,0
n2 = índice de refração do meio refrativo (a ser encontrado)
θ1 = ângulo de incidência = 30°
θ2 = ângulo de refração = 20°
Substituindo os valores conhecidos, temos:
Como fornecido pelo problema, 1,4 é a aproximação para .
Questão 5
(Enem 2015) A fotografia feita sob luz polarizada é usada por dermatologistas para diagnósticos. Isso permite ver detalhes da superfície da pele que não são visíveis com o reflexo da luz branca comum. Para se obter luz polarizada, pode-se utilizar a luz transmitida por um polaroide ou a luz refletida por uma superfície na condição de Brewster, como mostra a figura. Nessa situação, o feixe da luz refratada forma um ângulo de 90° com o feixe da luz refletida, fenômeno conhecido como Lei de Brewster. Nesse caso, o ângulo de incidência θp , também chamado de ângulo de polarização, e o ângulo de refração θr estão em conformidade com a Lei de Snell.
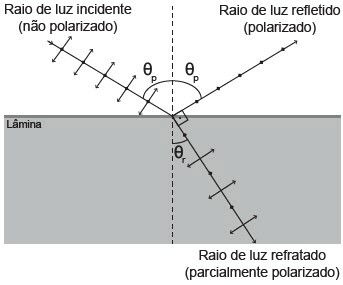
Considere:
Considere um feixe de luz não polarizada proveniente de um meio com índice de refração igual a 1, que incide sobre uma lâmina e faz um ângulo de refração θr de 30°.
Nessa situação, qual deve ser o índice de refração da lâmina para que o feixe refletido seja polarizado?
a) √3
b) √3/3
c) 2
d) 1/2
e) √3/2
Objetivo:
Determinar o índice de refração do segundo meio (lâmina) que atenda as condições do problema.
Dados:
Índice de refração n1 = 1;
Ângulo de refração 
= 30º.
Resolução:
Conforme a Lei de Snell: 
Onde:
- n1 é o índice de refração do meio incidente;
-
é o seno do ângulo de incidência; - n2 é o índice de refração do meio refringente;
-
é o seno do ângulo de refração.
A única variável que ainda não temos é o ângulo de incidência.
Pela imagem, temos que:
Substituindo o valor do ângulo de refração:
Podemos agora substituir os valores na Lei de Sell:
Questão 6
(UFPR 2018) Um dado meio tem um índice de refração n1. Um outro meio tem um índice de refração n2. Assinale a alternativa que expressa corretamente a relação entre os módulos das velocidades da luz nos dois meios, quando n2 = 2n1.
a) v2 = 4v1
b) v2 = 2v1.
c) v2 = v1.
d) 
e) 
O índice de refração é a razão entre a velocidade da luz no meio e no vácuo.
Onde n é o índice de refração, v é a velocidade da luz no meio e c é a velocidade da luz no vácuo.
O problema nos fornece a relação entre os índices de refração dos meios.
Isso significa que o índice de refração do segundo meio é o dobro do primeiro.
Substituindo a primeira equação na segunda:
Questão 7
(PUC 2019) No fundo de uma piscina, uma lâmpada verde gera um cone de luz muito bem definido, cujos raios se propagam para a superfície, como mostrado na figura.
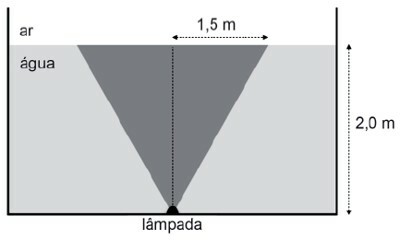
Qual é a profundidade aparente da lâmpada, em metros, vista por uma pessoa do lado de fora da piscina?
Dados
Índice de refração do ar = 1,0
Índice de refração da água = 4/3
a) 9/4
b) 9/8
c) 5/3
d) 4/5
e) 3/5
Conforme o enunciado, a água é o meio 1 e o ar é o meio 2, pois a luz está indo da água para o ar.
Dados:
Índice de refração do ar = 1,0 (meio 2)
Índice de refração da água = 4/3 (meio 1)
As medidas de 1,5 m e 2 m descritas na figura.
Objetivo:
Determinar a altura aparente percebida por um observador do lado de fora da piscina.
Este é o esquema da questão:
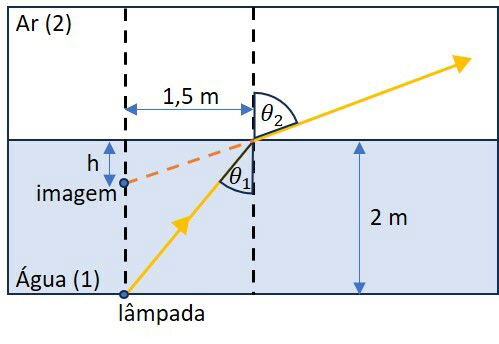
Precisamos determinar os ângulos de incidência e refração.
Pela Lei de Snell:
Para determinar 
aplicaremos o teorema de Pitágoras no seguinte triângulo:
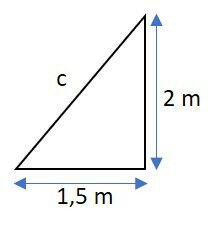
Onde c é a hipotenusa.
Para facilitar os cálculos, veja que 1,5 é igual a 3/2. Substituindo estes valores, temos:
Como seno é a razão entre o cateto oposto ao ângulo e a hipotenusa:
Retornando este resultado na equação da Lei de Snell:
Podemos determinar o seguinte triângulo retângulo congruente ao primeiro.
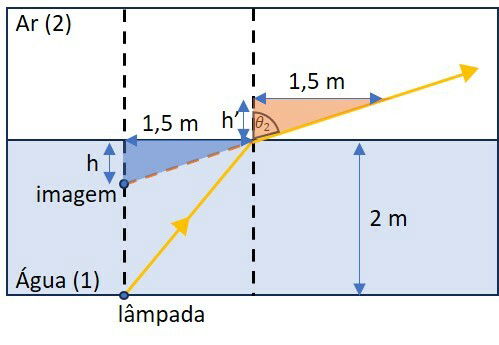
Temos que h = hʼ.
Usando a tangente de 
:
Já temos o 
e para determinar o cosseno, utilizaremos a relação fundamental da trigonometria.
Voltando para relação entre seno e cosseno:
Aprenda mais sobre Refração da Luz: o que é, leis e índice.
Você pode se interessar por:
- Luz - refração, reflexão e meios de propagação
- Luz: o que é e quais suas fontes
- Reflexão da Luz
- Ondas na Física: definição, tipos, fórmulas
- Exercícios sobre sombra e penumbra
ASTH, Rafael. Exercícios sobre refração da luz (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-refracao-da-luz/. Acesso em:
