ASSINAR TODA MATÉRIA+

Exercícios sobre temperatura e calor

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

Estude temperatura e calor com a lista de exercícios sobre: definição de temperatura e calor, dilatação e equilíbrio térmico, escalas termométricas, transferência de calor, calor latente e sensível. São diversos exercícios resolvidos e comentados para você aprender e tirar suas dúvidas.

Exercícios sobre definição de Temperatura e Calor

Exercício 1

Defina e diferencie temperatura e calor.

A Temperatura é a medida do estado térmico de um corpo ou sistema físico. Ele determina o grau de agitação das partículas que compõem este sistema.

A temperatura é, portanto, uma grandeza, algo que pode ser medido. No Sistema Internacional de Unidades, a unidade de medida de temperatura é o Kelvin (K). Outras unidades usuais são o Celsius (°C) e o Fahrenheit (°F).

Já o calor é o movimento da energia térmica. A energia térmica se transfere de corpos mais energéticos, com maior temperatura, para corpos e sistemas menos energéticos, com menor temperatura. Essa transferência de energia se dá por processos como: condução, convecção e irradiação.

Como calor é uma forma de energia, no Sistema Internacional de Unidades é medido em joules (J). Outra medida usual para calor é a caloria (cal).

A principal diferença entre temperatura e calor é que temperatura é a medida do estado térmico enquanto calor é a transferência da energia térmica entre os corpos.

Exercício 2

Defina o que é equilíbrio térmico.

Equilíbrio térmico é o estado em que diferentes corpos em um mesmo ambiente se encontram com a mesma temperatura, ou seja, possuam o mesmo estado térmico.

Como o calor é a transferência de energia térmica dos corpos mais quentes para os mais frios, os corpos antes mais quentes se esfriam a medida que cedem calor. Em contrapartida, os corpos que recebem este calor, antes mais frios, se esquentam.

Essa variação de temperaturas cessa quando não há mais calor entre os corpos, isso quer dizer que não há mais transferência de energia térmica entre eles. Neste estado, suas temperaturas são iguais.

Exercício 3

Explique o seguinte fenômeno:

Laura acaba de acordar e levantar de sua cama em um frio dia de inverno. Após sair de sua cama aquecida, ela toca os pés no chão de carpete de seu quarto e se sente confortável, mesmo descalça. Ao ir para cozinha, seus pés descalços sentem uma sensação fria ao tocar o chão de cerâmica.

Todo o ambiente da casa estava exposto às mesmas condições de temperatura durante toda noite. Por que Laura sente sensações diferentes ao caminhar descalça no quarto e na cozinha?

As sensações de quente e frio estão relacionadas à diversos fatores, alguns até mesmo subjetivos. Pessoas diferentes podem sentir e perceber uma mesma temperatura de formas diferentes. No entanto, no texto, a mesma pessoa tem sensações diferentes em um ambiente que se supõe estar em equilíbrio térmico, isto é, onde os corpos estão a mesma temperatura.

A única diferença é o material com que ela entra em contato. O coeficiente de condutibilidade térmica é uma propriedade dos materiais e indicam o grau de facilidade com que a energia térmica se transfere. Quanto mais o valor da condutibilidade térmica, mais fácil é a transferência de energia térmica.

Como o chão cerâmico possui maior condutibilidade térmica do que o carpete de lã ou algodão, o corpo de Laura perde uma quantidade maior de energia quando caminha pela cozinha do que quando caminha pelo carpete, o que faz ela interpretar que o chão esteja mais frio.

Exercícios Sobre Equilíbrio Térmico

Exercício 4

(IFF 2016) Na atividade de laboratório, o professor de Física propõe que os estudantes misturem 1L de água à temperatura de 100°C com 500 mL de água a 4°C. Porém, antes de fazer a mistura e medir a temperatura de equilíbrio térmico, os estudantes precisam calcular a temperatura do equilíbrio térmico. Considere as perdas térmicas desprezíveis e que o resultado teórico é igual ao valor experimental. Pode-se afirmar que essa temperatura de equilíbrio vale:

a) 68°C.
b) 74°C.
c) 80°C.
d) 32°C.
e) 52°C.

Resposta correta: a) 68°C.

Objetivo: determinar a temperatura de equilíbrio térmico (T com f subscrito).

Dados:
1L = 1 000 ml de água a 100°C;
500 ml de água a 4°C

Modelo físico e matemático

No equilíbrio térmico não há mais transferência de energia térmica, por isso, a soma dos calores das porções de água a 100°C e 4°C, é igual a zero.

Q com 100 subscrito espaço mais espaço Q com 4 subscrito espaço igual a espaço 0

m com 100 subscrito espaço. espaço c com á g u a subscrito fim do subscrito espaço. espaço incremento teta espaço mais espaço m com 4 subscrito espaço. espaço c com á g u a subscrito fim do subscrito espaço. espaço incremento teta espaço igual a espaço 0 1 espaço 000 espaço. espaço c com á g u a subscrito fim do subscrito espaço. espaço parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito espaço mais espaço 500 espaço. espaço c com á g u a subscrito fim do subscrito espaço. espaço parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito espaço igual a espaço 0 1 espaço 000 espaço c com á g u a subscrito fim do subscrito espaço parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito espaço igual a espaço menos espaço espaço 500 espaço c com á g u a subscrito fim do subscrito espaço parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito

Como nos dois lados da equação o calor específico é o mesmo, podemos cancelá-los.

1 espaço 000 espaço riscado diagonal para cima sobre c com á g u a subscrito fim do subscrito fim do riscado espaço parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito espaço igual a espaço menos espaço 500 espaço riscado diagonal para cima sobre c com á g u a subscrito fim do subscrito fim do riscado espaço parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito 1 espaço 000 espaço parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito espaço igual a espaço menos espaço 500 espaço parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito numerador 1 espaço 000 sobre denominador menos espaço 500 fim da fração parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito igual a espaço parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito menos espaço 2 espaço parêntese esquerdo T com f subscrito espaço menos espaço 100 parêntese direito igual a parêntese esquerdo T com f subscrito espaço menos espaço 4 parêntese direito menos espaço 2 espaço T com f subscrito espaço mais espaço 200 espaço igual a T com f subscrito espaço menos espaço 4 200 espaço mais espaço 4 espaço igual a espaço T com f subscrito espaço mais espaço 2 T com f subscrito 204 espaço igual a espaço 3 T com f subscrito 204 sobre 3 igual a T com f subscrito 68 espaço igual a espaço T com f subscrito

Portanto, a temperatura de equilíbrio será de 68°C.

Exercícios Sobre Escalas Termométricas

Exercícios 5

(SENAC - SP 2013) A chegada do homem a lua aconteceu em 1969. A estrutura da lua é rochosa e praticamente não possui atmosfera, o que faz com que durante o dia a temperatura chegue a 105 °C e à noite caia para −155 °C.

Essa variação térmica, medida na escala Fahrenheit de temperatura, vale

a) 50.
b) 90.
c) 292.
d) 468.
e) 472.

Resposta correta: d) 468.

A relação entre a escala Celsius °C e a escala °F é dada por:

numerador incremento teta sinal de grau C sobre denominador 100 fim da fração igual a numerador incremento teta sinal de grau F sobre denominador 180 fim da fração

Onde,

incremento teta sinal de grau C é a variação da temperatura em graus Celsius e,

incremento teta sinal de grau F é a variação em Fahrenheit.

A temperatura na superfície lunar varia entre 105°C e a noite -155°C. Sendo assim, a variação total é de 260°C.

105 - (-155) = 260

Substituindo na fórmula, temos:

260 sobre 100 igual a numerador incremento teta sinal de grau F sobre denominador 180 fim da fração numerador 260 espaço. espaço 180 sobre denominador 100 fim da fração igual a incremento teta sinal de grau F 468 espaço igual a espaço incremento teta sinal de grau F

Exercícios 6

(UESPI 2010) Um estudante está lendo o romance de ficção científica “Fahrenheit 451”, de Ray Bradbury. Num certo trecho, uma das personagens afirma que 451 °F é a temperatura na escala Fahrenheit em que o papel de que são feitos os livros entra em combustão. O estudante sabe que, nesta escala, as temperaturas de fusão e ebulição da água são respectivamente iguais a 32 °F e 212 °F. Ele conclui, acertadamente, que 451 °F é aproximadamente equivalente a:

a) 100 °C
b) 205 °C
c) 233 °C
d) 305 °C
e) 316 °C

Resposta correta: c) 233 °C.

As escalas Celsius e Fahrenheit se relacionam por:

numerador teta sinal de grau C sobre denominador 5 fim da fração igual a numerador teta sinal de grau F espaço menos espaço 32 sobre denominador 9 fim da fração

Substituindo 451°F por teta sinal de grau F, temos:

numerador teta sinal de grau C sobre denominador 5 fim da fração igual a numerador 451 espaço menos espaço 32 sobre denominador 9 fim da fração numerador teta sinal de grau C sobre denominador 5 fim da fração igual a 419 sobre 9 teta sinal de grau C igual a numerador 419 espaço. espaço 5 sobre denominador 9 fim da fração espaço aproximadamente igual espaço 232 vírgula 7

Das opções de resposta 233°C é a mais próxima.

Exercícios 7

(FATEC 2014) Durante uma corrida de Formula Indy ou de Fórmula 1, os pilotos ficam sujeitos a um microambiente quente no cockpit que chega a atingir 50ºC, gerado por diversas fontes de calor (do Sol, do motor, do terreno, do metabolismo cerebral, da atividade muscular etc.). Essa temperatura está muito acima da temperatura corporal média tolerável, por isso, eles devem se manter sempre com bom condicionamento físico.

As corridas de Fórmula Indy são mais tradicionais nos EUA, onde se adota a leitura da temperatura na escala Fahrenheit. Baseado nas informações apresentadas no texto, é correto afirmar que a temperatura do cockpit que um carro de Fórmula Indy chega a atingir durante a corrida, em grau Fahrenheit, é

Dados:
Temperatura de fusão do gelo = 32 ºF;
Temperatura de ebulição da água = 212 ºF.

a) 32.
b) 50.
c) 82.
d) 122.
e) 212.

Resposta correta: d) 122

Para relacionar as duas temperaturas, utilizamos a equação:

numerador teta sinal de grau C sobre denominador 5 fim da fração igual a numerador teta sinal de grau F espaço menos espaço 32 sobre denominador 9 fim da fração

Substituindo teta sinal de grau C por 50 e resolvendo para teta sinal de grau F , temos:

50 sobre 5 igual a numerador teta sinal de grau F espaço menos espaço 32 sobre denominador 9 fim da fração 10 espaço igual a numerador teta sinal de grau F espaço menos espaço 32 sobre denominador 9 fim da fração 10 espaço. espaço 9 espaço igual a espaço teta sinal de grau F espaço menos espaço 32 90 espaço igual a espaço teta sinal de grau F espaço menos espaço 32 90 espaço mais espaço 32 espaço igual a espaço teta sinal de grau F 122 espaço igual a espaço teta sinal de grau F

Portanto, a temperatura no cockpit, em Fahrenheit é de 122°F.

Exercícios Sobre Propagação do Calor

Exercício 8

(Enem 2021) Em um manual de instruções de uma geladeira, constam as seguintes recomendações:

• Mantenha a porta de seu refrigerador aberta apenas o tempo necessário;

• É importante não obstruir a circulação do ar com a má distribuição dos alimentos nas prateleiras;

• Deixe um espaço de, no mínimo, 5 cm entre a parte traseira do produto (dissipador serpentinado) e a parede.

Com base nos princípios da termodinâmica, as justificativas para essas recomendações são, respectivamente:

a) Reduzir a saída de frio do refrigerador para o ambiente, garantir a transmissão do frio entre os alimentos na prateleira e permitir a troca de calor entre o dissipador de calor e o ambiente.

b) Reduzir a saída de frio do refrigerador para o ambiente, garantir a convecção do ar interno, garantir o isolamento térmico entre a parte interna e a externa.

c) Reduzir o fluxo de calor do ambiente para a parte interna do refrigerador, garantir a convecção do ar interno e permitir a troca de calor entre o dissipador e o ambiente.

d) Reduzir o fluxo de calor do ambiente para a parte interna do refrigerador, garantir a transmissão do frio entre os alimentos na prateleira e permitir a troca de calor entre o dissipador e o ambiente.

e) Reduzir o fluxo de calor do ambiente para a parte interna do refrigerador, garantir a convecção do ar interno e garantir o isolamento térmico entre as partes interna e externa.

Resposta correta: c) Reduzir o fluxo de calor do ambiente para a parte interna do refrigerador, garantir a convecção do ar interno e permitir a troca de calor entre o dissipador e o ambiente.

  • Manter a porta do refrigerador fechada, abrindo apenas o necessário, evita a entrada de calor proveniente do ambiente externo.

  • Dentro da geladeira, as trocas de calor entre o ambiente interno frio e os alimentos produzem correntes de ar, por meio da convecção. Estas correntes são necessárias para o resfriamento dos alimentos.

  • O calor retirado dos alimentos e trocado com o fluido refrigerante da geladeira é transportado ao dissipador que fica na parte de traz. Este calor será trocado com o ambiente, principalmente por convecção, por isso o espaço é necessário.

Exercício 9

(UEPB 2009) Uma criança que gostava de brigadeiro decidiu fazer este doce, e para isso começou a separar os ingredientes e utensílios. Inicialmente pegou a lata de leite condensado, o chocolate em pó e a margarina, depois uma panela e colher de aço e um abridor de latas. A criança fez um furo na lata, a fim de fazer escoar para a panela o leite condensado. Sua mãe, ao ver aquela atitude, sugeriu que o filho fizesse outro furo na lata, pois assim ele conseguiria retirar aquele líquido com mais facilidade. Ao levar a panela ao fogo para mexer o brigadeiro, a criança sentiu que, depois de alguns minutos, o cabo da colher tinha se aquecido e reclamou: “Mãe, a colher está queimando a minha mão”. Então, sua mãe pediu que ele fizesse uso de uma colher de pau, para evitar uma queimadura.

Sobre o aquecimento da colher evidenciado na reclamação da criança de que sua mão estava queimando, podemos afirmar que

a) com a colher de pau, que é um excelente isolante térmico, esta aquece-se mais rápido que a colher de aço.

b) acontece porque as partículas que constituem a colher criam correntes de convecção, aquecendo-a por inteiro, de uma extremidade à outra.

c) devido a irradiação a colher se aquece por inteiro, de uma extremidade à outra.

d) com a colher de pau, que é um excelente condutor térmico, esta aquece-se mais rápido que a colher de aço.

e) acontece porque as partículas que constituem a colher passam a conduzir de uma extremidade a outra o calor ali absorvido.

Resposta correta: e) acontece porque as partículas que constituem a colher passam a conduzir de uma extremidade a outra o calor ali absorvido.

O processo de propagação de calor é a condução. Apenas a energia é transferida de uma partícula às de sua vizinhança. Os metais são excelentes transmissores de calor.

Exercício 10

(Enem 2016) Num experimento, um professor deixa duas bandejas de mesma massa, uma de plástico e outra de alumínio, sobre a mesa do laboratório. Após algumas horas, ele pede aos alunos que avaliem a temperatura das duas bandejas, usando para isso o tato. Seus alunos afirmam, categoricamente, que a bandeja de alumínio encontra-se numa temperatura mais baixa. Intrigado, ele propõe uma segunda atividade, em que coloca um cubo de gelo sobre cada uma das bandejas, que estão em equilíbrio térmico com o ambiente, e os questiona em qual delas a taxa de derretimento do gelo será maior.

O aluno que responder corretamente ao questionamento do professor dirá que o derretimento ocorrerá

a) mais rapidamente na bandeja de alumínio, pois ela tem uma maior condutividade térmica que a de plástico.

b) mais rapidamente na bandeja de plástico, pois ela tem inicialmente uma temperatura mais alta que a de alumínio.

c) mais rapidamente na bandeja de plástico, pois ela tem uma maior capacidade térmica que a de alumínio.

d) mais rapidamente na bandeja de alumínio, pois ela tem um calor específico menor que a de plástico.

e) com a mesma rapidez nas duas bandejas, pois apresentarão a mesma variação de temperatura.

Resposta correta: a) mais rapidamente na bandeja de alumínio, pois ela tem uma maior condutividade térmica que a de plástico.

O gelo derrete mais rápido na bandeja que transfere calor a uma maior taxa, ou seja, mais rápido. Como os metais possuem maior condutibilidade térmica, a bandeja de alumínio transfere mais calor ao gelo e ele derreterá mais rápido.

Exercício 11

(Enem 2021) Na cidade de São Paulo, as ilhas de calor são responsáveis pela alteração da direção do fluxo da brisa marítima que deveria atingir a região de mananciais. Mas, ao cruzar a ilha de calor, a brisa marítima agora encontra um fluxo de ar vertical, que transfere para ela energia térmica absorvida das superfícies quentes da cidade, deslocando-a para altas altitudes. Dessa maneira, há condensação e chuvas fortes no centro da cidade, em vez de na região de mananciais. A imagem apresenta os três subsistemas que trocam energia nesse fenômeno.

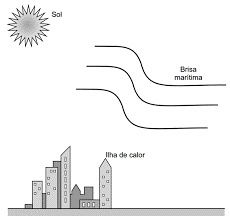
Imagem associada a resolução da questão.

Esses mecanismos são, respectivamente,

a) irradiação e convecção.
b) irradiação e irradiação.
c) condução e irradiação.
d) convecção e irradiação.
e) convecção e convecção.

Resposta correta: a) irradiação e convecção.

Irradiação é processo de transferência de calor entre o Sol e as cidades. Neste processo, o calor é transferido por radiação eletromagnética.

Convecção é o processo de transferência de calor entre as ilhas de calor e a brisa marítima. Neste processo, o calor é transferido por um meio fluido, no caso, o ar, através de seus movimentos. Na convecção o ar quente que se expande, fica menos denso e sobe. O ar mais frio nas altitudes superiores, mais denso, desce criando correntes de ar que trocam calor.

Exercícios Sobre Calor Latente e Calor Sensível

Exercício 12

(Enem 2015) As altas temperaturas de combustão e o atrito entre suas peças móveis são alguns dos fatores que provocam o aquecimento dos motores à combustão interna. Para evitar o superaquecimento e consequentes danos a esses motores, foram desenvolvidos os atuais sistemas de refrigeração, em que um fluido arrefecedor com propriedades especiais circula pelo interior do motor, absorvendo o calor que, ao passar pelo radiador, é transferido para a atmosfera.

Qual propriedade o fluido arrefecedor deve possuir para cumprir seu objetivo com maior eficiência?

a) Alto calor específico.
b) Alto calor latente de fusão.
c) Baixa condutividade térmica.
d) Baixa temperatura de ebulição.
e) Alto coeficiente de dilatação térmica.

Resposta correta: a) Alto calor específico.

Calor específico é uma propriedade do material, no caso, o fluido refrigerador. Ele indica a quantidade de calor que ele precisa receber ou ceder para uma unidade de massa, variar uma unidade de temperatura.

Em outras palavras, quanto maior a calor específico, mais calor ele pode receber sem aumentar muito sua temperatura. Substâncias com alto calor específico possuem menor sensibilidade a mudança de temperatura.

Desta forma, o líquido refrigerante com alto calor específico pode "recolher" maior quantidade de energia térmica do motor sem entrar em ebulição.

Exercício 13

(FATEC 2014) Em uma aula da disciplina de Física no curso de Soldagem da Fatec, o docente responsável retoma com os alunos um tópico visto por eles no Ensino Médio. Explica como efetuar a análise de um gráfico de mudança de estado de uma determinada substância pura hipotética. Para isso, basta avaliarmos as grandezas físicas representadas nos eixos e o gráfico formado pela relação entre essas grandezas. Nesse gráfico, o trecho que apresenta inclinação indica mudança de temperatura por absorção de energia, e o que apresenta platô (trecho horizontal) indica mudança de estado por absorção de energia.

Após essa explicação, ele pergunta aos alunos qual foi a quantidade total de energia absorvida pela substância entre o fim da mudança de estado para o líquido, até o fim da mudança de estado para o gasoso.

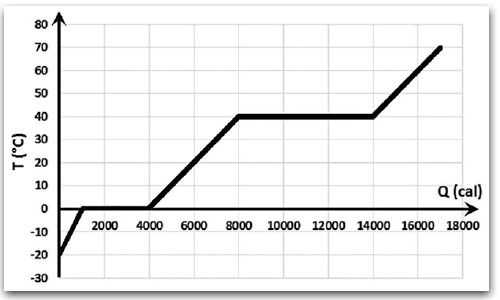
Imagem associada a resolução da questão.

A resposta correta a essa pergunta, em calorias, é

a) 2 000.
b) 4 000.
c) 6 000.
d) 10 000.
e) 14 000.

Resposta correta: d) 10 000.

Esta mudança ocorre entre as 4000 e 14000 calorias. A substância está totalmente em estado líquido quando começa a rampa, após o primeiro platô. A transformação da fase líquida para gasosa acorre no segundo platô.

Exercícios Sobre Dilatação Térmica

Exercício 14

(URCA 2012) O raio da base de um cone metálico, cuja densidade é igual a 10 g/cm3 , tem a 0°C um comprimento inicial Ro = 2 cm. Aquecendo­-se este cone até uma temperatura de 100°C a sua altura sofre uma variação Δh = 0,015 cm. Sendo a massa do cone de 100 g, o coeficiente de dilatação linear médio do material vale:

a parêntese direito espaço 6 espaço x espaço 10 à potência de menos 4 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial

b parêntese direito espaço 6 espaço x espaço 10 à potência de menos 5 espaço fim do exponencial sinal de grau C à potência de menos 1 fim do exponencial

c parêntese direito espaço 5 espaço x espaço 10 à potência de menos 4 espaço fim do exponencial sinal de grau C à potência de menos 1 fim do exponencial

d parêntese direito espaço 5 espaço x espaço 10 à potência de menos 5 espaço fim do exponencial sinal de grau C à potência de menos 1 fim do exponencial

e parêntese direito espaço 4 espaço x espaço 10 à potência de menos 4 espaço fim do exponencial sinal de grau C à potência de menos 1 fim do exponencial

Resposta correta: b parêntese direito espaço 6 espaço x espaço 10 à potência de menos 5 espaço fim do exponencial sinal de grau C à potência de menos 1 fim do exponencial

Objetivo: determinar o coeficiente de dilatação linear (alfa).

Dados
incremento h = 0,015 cm
Raio inicial, = 2 cm
incremento teta = 100°C
massa, m = 100 g
densidade, d = 10 g/cm3

Modelo matemático e físico da dilatação térmica linear
incremento h igual a h com i subscrito. alfa. incremento teta

Onde,
alfa é o coeficiente de dilatação linear.
incremento h é a variação da altura.
h com i subscrito é a altura inicial.
incremento teta é a variação da temperatura.

Isolando alfa,

alfa igual a numerador incremento h sobre denominador h com i subscrito. incremento teta fim da fração

incremento teta espaço e incremento h são fornecidos. Desta forma, para determinar alfa, é preciso determinar h com i subscrito.

Para determinar h com i subscrito vamos utilizar as relações do volume e da densidade.

Volume do cone

V igual a numerador á r e a espaço d a espaço b a s e espaço. espaço a l t u r a sobre denominador 3 fim da fração V com i subscrito espaço igual a espaço numerador pi. r com i subscrito ao quadrado. h com i subscrito sobre denominador 3 fim da fração

Densidade
d igual a m sobre V

Isolando V,
V espaço igual a espaço m sobre d igual a 100 sobre 10 igual a 10 espaço c m ao cubo

Substituindo o valor de V e r na equação do volume e fazendo pi = 3,
V com i subscrito espaço igual a espaço numerador pi. r com i subscrito ao quadrado. h com i subscrito sobre denominador 3 fim da fração 10 espaço igual a numerador 3 espaço. espaço 2 ao quadrado espaço. espaço h com i subscrito sobre denominador 3 fim da fração 10 espaço. espaço 3 espaço igual a espaço 3 espaço. espaço 4 espaço. espaço h com i subscrito 30 sobre 12 igual a h com i subscrito 2 vírgula 5 espaço igual a espaço h com i subscrito

Agora podemos substituir h com i subscrito na equação do coeficiente de dilatação térmica,

alfa igual a numerador incremento h sobre denominador h com i subscrito. incremento teta fim da fração alfa igual a numerador 0 vírgula 015 sobre denominador 2 vírgula 5.100 fim da fração igual a 0 vírgula 00006 espaço

Transformando em notação científica

0,0006 = 6 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial

Aprenda mais sobre

Para mais exercícios de Física:

Exercícios de Física (resolvidos) para 2º ano do ensino médio

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Exercícios de Física
Que tal um up?
Toda Matéria+
Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo
Exercícios exclusivos Acesso a centenas de questões com gabaritos
Estude sem publicidade Navegação limpa e focada para evitar distrações
Assinar Toda Matéria+
Toda Matéria no YouTube
Thumbnail Toda Matéria no Youtube
Toda Matéria Inscreva-se