Vetores
Vetor é a representação que determina o módulo, a direção e o sentido de uma grandeza vetorial. Os vetores são segmentos de reta orientados por uma seta em uma extremidade.
Nomeamos os vetores com uma letra e uma pequena seta.
Os vetores caracterizam as grandezas vetoriais, que são as grandezas que precisam de orientação, ou seja, direção e sentido. Alguns exemplos são: força, velocidade, aceleração e deslocamento. Não basta o valor numérico, é preciso descrever para onde atuam estas grandezas.
Módulo de um vetor
O módulo do vetor, ou intensidade, é seu valor numérico, seguido da unidade de medida da grandeza que ele representa, por exemplo:
Indicamos o módulo entre barras mantendo a seta ou, apenas a letra, sem barras e sem seta.
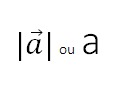
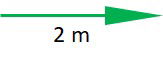
O comprimento do vetor é proporcional ao módulo. Um vetor maior representa um módulo maior.
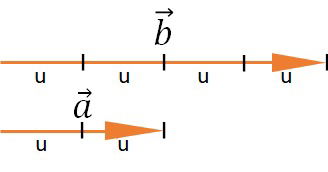
O módulo do vetor é de 4 unidades, enquanto do vetor
é de 2 unidades.
Direção de um Vetor
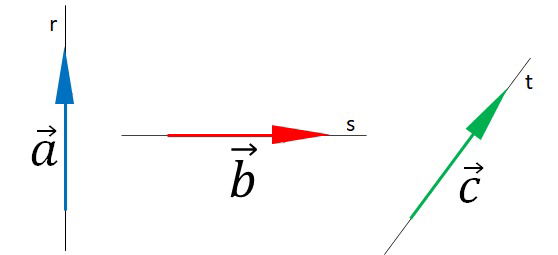
A direção do vetor é a inclinação da reta suporte em que ele está determinado. Só existe uma direção para cada vetor.
Sentido de um Vetor
O sentido do vetor é mostrado pela seta. Uma mesma direção pode conter dois sentidos, como para cima ou para baixo e, para a direita ou esquerda.
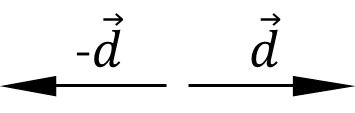
Adotando um sentido como positivo, o sentido oposto, o negativo, é representado com um sinal de subtração antes do símbolo do vetor.
Vetor Resultante
O vetor resultante é resultado de operações vetoriais e, equivale a um conjunto de vetores. É conveniente conhecer o vetor que representa o efeito produzido por mais de um vetor.
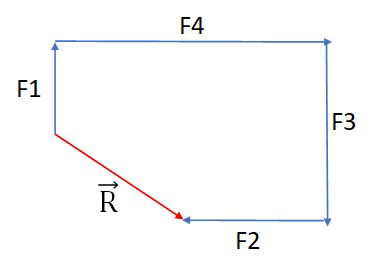
Por exemplo, um corpo pode estar sujeito a um conjunto de forças e, querermos saber o resultado que irão produzir, todas juntas, sobre este corpo. Cada força é representada por um vetor, mas o resultado pode ser representado por apenas um vetor: o vetor resultante.
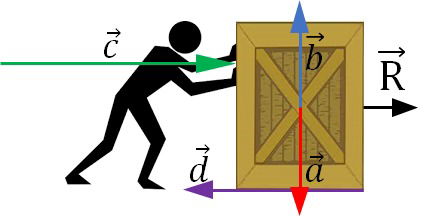
O vetor resultante, , de direção horizontal e sentido para a direita, é o resultado de somas e subtrações dos vetores
,
,
e
. O vetor resultante mostra uma tendência ao corpo se mover com esta orientação.
Os vetores com direção vertical, possuem o mesmo tamanho, ou seja, o mesmo módulo. Como possuem sentidos opostos eles se anulam. Isto mostra que não haverá movimento do caixote na direção vertical.
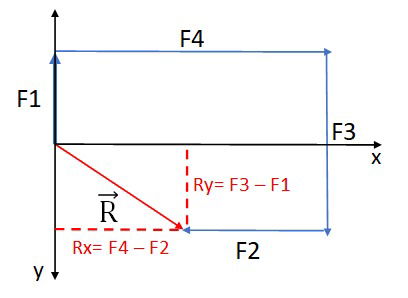
Ao analisar os vetores e
, que possuem mesma direção e sentidos opostos, percebemos que "sobra" uma parte da força para a direita, pois o vetor
é maior que o
, ou seja, o módulo de
é maior.
Para determinar o vetor resultante, realizamos operações de soma e subtração de vetores.
Soma e subtração de vetores com mesma direção
Com sentidos iguais, somamos os módulos e mantemos a direção e o sentido.
Exemplo:
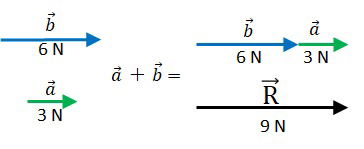
Graficamente colocamos os vetores em sequência, sem alterar seus módulos. O início de um deve coincidir com o final do outro.
Vale a propriedade comutativa da adição, pois a ordem não altera o resultado.
Com sentidos opostos, subtraímos os módulos e mantemos a direção. O sentido do vetor resultante é o do vetor com maior módulo.
Exemplo:
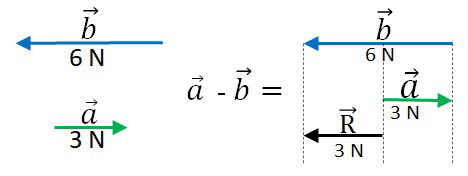
O vetor é a parte que sobra de
, após retirar
.
Subtrair um vetor equivale a somar com o oposto do outro.
Soma e Subtração de Vetores Perpendiculares
Para somar dois vetores com direções perpendiculares, movimentamos os vetores sem alterar seus módulos, de modo que o início de um coincida o final do outro.
O vetor resultante liga o início do primeiro ao final do segundo.
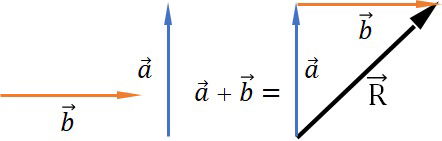
Para determinar o módulo do vetor resultante entre dois vetores perpendiculares, fazemos coincidir o início dos dois vetores.
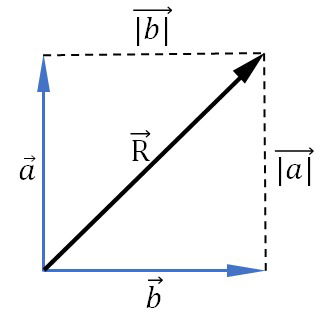
O módulo do vetor resultante é determinado pelo teorema de Pitágoras.
Soma e subtração de vetores oblíquos
Dois vetores são oblíquos quando formam um ângulo entre suas direções, diferente de 0°, 90° e 180°. Para somar ou subtrair vetores oblíquos utilizam-se os métodos do paralelogramo e linha poligonal.
Método do paralelogramo
Para realizar o método, ou regra, do paralelogramo entre dois vetores e, desenhar o vetor resultante, seguimos os seguintes passos:
O primeiro passo é posicionar suas origens no mesmo ponto e traçarmos retas paralelas aos vetores, para formar um paralelogramo.
O segundo é traçar um vetor diagonal no paralelogramo, entre a união dos vetores e a união das retas paralelas.
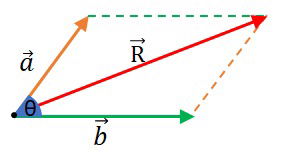
As linhas pontilhadas são paralelas aos vetores e a figura geométrica formada é um paralelogramo.
O vetor resultante é a linha que liga a origem dos vetores ao encontro das paralelas.
O módulo do vetor resultante é obtido pela Lei dos Cossenos.
Onde:
R é o módulo do vetor resultante;
a é o módulo do vetor ;
b é o módulo do vetor ;
é o ângulo formado entre as direções dos vetores.
O método do paralelogramo é utilizado para somar um par de vetores. Caso se queira somar mais de dois vetores, devemos somá-los dois a dois. Ao vetor resultante da soma dos dois primeiros, somamos o terceiro e assim por diante.
Outra forma de somar mais de dois vetores é usar o método da linha poligonal.
Método da linha poligonal
O método da linha poligonal é utilizado para encontrar o vetor resultante da adição de vetores. Este método é especialmente útil ao somar mais de dois vetores, como os seguintes vetores ,
,
e
.
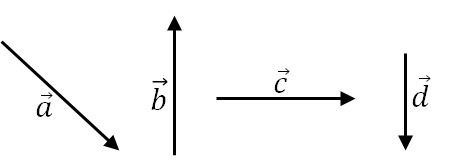
Para utilizar este método devemos ordenar os vetores de modo que o final de um (seta), coincida com o início de outro. É importante conservar o módulo, a direção e o sentido.
Após organizar todos os vetores na forma de uma linha poligonal, devemos traçar o vetor resultante que vai do início do primeiro até o final do último.
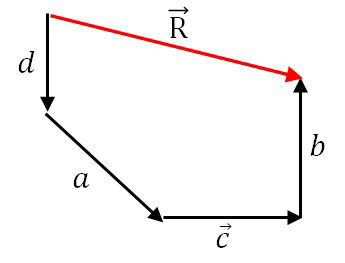
É importante que o vetor resultante feche o polígono, com sua seta coincidindo com a seta do último vetor.
A propriedade comutativa é válida, pois a ordem que posicionamos os vetores-parcelas não altera o vetor resultante.
Decomposição Vetorial
Decompor um vetor é escrever os componentes que formam este vetor. Esses componentes são outros vetores.
Todo vetor pode ser escrito como uma composição de outros vetores, através de uma soma vetorial. Em outras palavras, podemos escrever um vetor como sendo resultante da soma de dois vetores, que chamamos componentes.
Utilizando um sistema cartesiano de coordenadas, com eixos x e y perpendiculares, determinamos os componentes do vetor.
O vetor é resultante da soma vetorial entre os vetores componentes
e
.
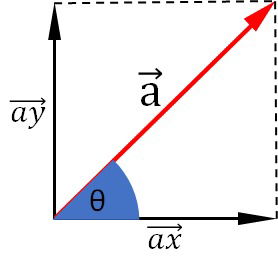
O vetor de inclinação
forma um triângulo retângulo com o eixo x. Assim, determinamos os módulos dos vetores componentes utilizando trigonometria.
Módulo do componente ax.
Módulo do componente ay.
O módulo do vetor é obtido pelo Teorema de Pitágoras.
Exemplo
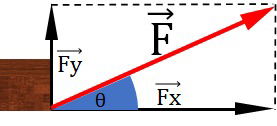
Uma força é realizada ao puxar um bloco no chão. A força de módulo 50 N tem inclinação de 30° com a horizontal. Determine as componentes horizontal e vertical desta força.
Dados:
Multiplicação de um número real por um vetor
Ao multiplicar um número real por um vetor, o resultado será um novo vetor, que possui as seguintes características:
- Mesma direção, se o número real for diferente de zero;
- Mesmo sentido, se o número real for positivo e, sentido contrário se for negativo;
- O módulo será o produto entre o módulo do número real e o módulo do vetor multiplicado.
Produto entre um número real e um vetor
Onde:
é o vetor resultante da multiplicação;
é o número real;
é o vetor que está sendo multiplicado.
Exemplo
Seja o número real n = 3 e o vetor de módulo 2, o produto entre eles é igual a:
Cálculo do módulo
A direção e o sentido serão os mesmos.
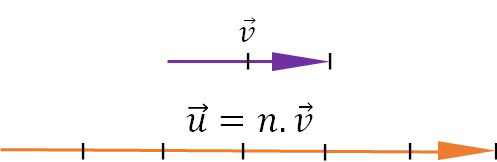
Exercício 1
(Enem 2011) A força de atrito é uma força que depende do contato entre corpos. Pode ser definida como uma força de oposição à tendência de deslocamento dos corpos e é gerada devido a irregularidades entre duas superfícies em contato. Na figura, as setas representam forças que atuam no corpo e o ponto ampliado representa as irregularidades que existem entre as duas superfícies.
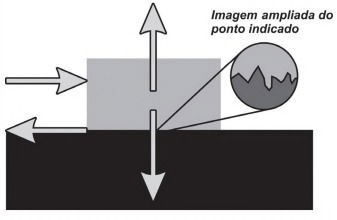
Na figura, os vetores que representam as forças que provocam o deslocamento e o atrito são, respectivamente:
a) ![]()
b) 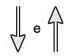
c) ![]()
d) 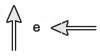
e) 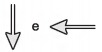
Exercício 2
(UEFS 2011) O diagrama vetorial da figura esquematiza as forças exercidas por dois elásticos em um dente de uma pessoa que faz tratamento ortodôntico.
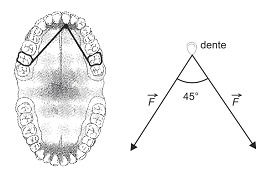
Admitindo-se F = 10,0N, sen45° = 0,7 e cos45° = 0,7, a intensidade da força aplicada pelos elásticos no dente, em N, é igual a
a) 3√10
b) 2√30
c) 2√85
d) 3√35
e) 2√45
Exercício 3
(PUC RJ 2016) As forças F1 , F2 , F3 e F4 , na Figura, fazem ângulos retos entre si e seus módulos são, respectivamente, 1 N, 2 N, 3 N e 4 N.
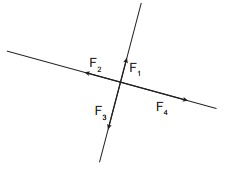
Calcule o módulo da força resultante, em N.
a) 0
b) √2
c) 2
d) 2√ 2
e) 10
Aprenda mais sobre
Pratique com:
ASTH, Rafael. Vetores. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/fisica-vetores/. Acesso em: