Acelere seu aprendizado

Força Centrípeta: o que é, fórmulas e exemplos

Rafael C. Asth

Professor de Matemática e Física

A força centrípeta é a força que age sobre os corpos no movimento circular em determinada trajetória curvilínea.

Através dela, é possível mudar a direção da velocidade de um corpo em uma trajetória circular, atraindo-o para o centro.

Fórmulas da força centrípeta

Como enunciado pela 2ª Lei de Newton, força é o produto entre a massa do corpo por sua aceleração.

$começar estilo tamanho matemático 20px reto F com reto c subscrito igual a reto m sinal de multiplicação reto a com reto c subscrito espaço fim do estilo$

Onde,

$começar estilo tamanho matemático 16px reto F com reto c subscrito fim do estilo$ é a Força centrípeta, em newton (N);
$começar estilo tamanho matemático 16px reto a com reto c subscrito fim do estilo$ é a aceleração centrípeta;
m: massa, em quilograma (Kg)

Em muitos problemas é preciso calcular a aceleração centrípeta, sendo ela a divisão entre a velocidade ao quadrado e o raio da trajetória circular.

$começar estilo tamanho matemático 20px reto a com reto c subscrito igual a reto v ao quadrado sobre reto r fim do estilo$

Onde,

v: velocidade, em metros por segundo (m/s)
r: raio da trajetória circular, em metros (m)

Juntando as duas fórmulas, obtemos:

$Error converting from MathML to accessible text.$

Força centrípeta: Segunda Lei de Newton e a aceleração centrípeta

A fórmula da força centrípeta deriva da Segunda Lei de Newton, também chamada de Princípio Fundamental da Dinâmica, que diz:

“A aceleração (a) adquirida por um corpo é diretamente proporcional à força resultante (F_r) que atua sobre ele.”

A massa do objeto (m) pode ser interpretada a constante de proporcionalidade da equação e representa a medida da inércia do corpo.

Se a mesma força for aplicada em dois corpos de massas diferentes, o corpo de menor massa sofrerá uma aceleração maior.

Para calcular a força centrípeta, a aceleração (a) utilizada na fórmula é a aceleração centrípeta (ac), também chamada de aceleração radial, que atua nos corpos que realizam uma trajetória circular.

Essa grandeza aponta para o centro da curvatura, sendo perpendicular à velocidade do corpo.

Portanto, substituindo a fórmula da aceleração centrípeta na fórmula de força resultante da Segunda Lei de Newton, temos a fórmula da força centrípeta.

Exemplo de aplicação da força centrípeta

O globo da morte é uma grande esfera metálica utilizada como atração em circos, por exemplo, para um motociclista realizar movimentos no espaço.

Quando uma pessoa movimenta-se com sua moto em um globo da morte, ela precisa aplicar uma velocidade mínima para não cair ao dar uma volta completa.

Observe as forças que atuam sobre um motociclista ao percorrer o globo da morte.

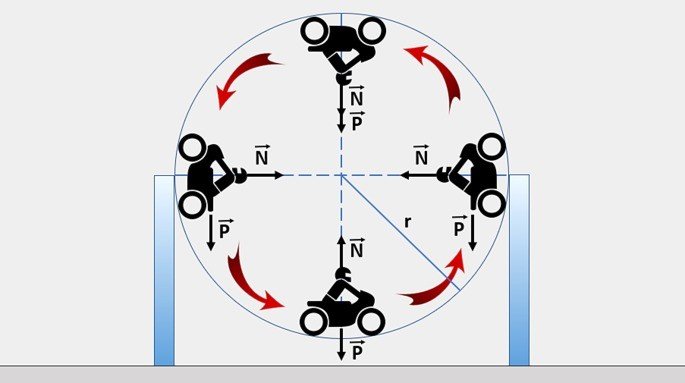
Observe que a força peso (P) sempre aponta para baixo, enquanto a força normal (N) aponta para o centro da esfera.

No movimento circular realizado, a velocidade é constante, mas a direção e o sentido do vetor variam,, ao mudarem com a aceleração centrípeta.

Na direção do raio da trajetória, a força centrípeta é dada pela soma das forças que atuam sobre o corpo.

Exemplo resolvido:

Considere a imagem do globo da morte e os dados: r = 2,0 m; m = 150 kg (homem + moto) e v = 6,0 m/s (velocidade no ponto mais alto). Determine a força centrípeta do conjunto motociclista e motocicleta neste ponto.

$Fc igual a numerador 150 espaço kg espaço. espaço parêntese esquerdo 6 espaço reto m dividido por reto s parêntese direito ao quadrado sobre denominador 2 espaço reto m fim da fração Fc igual a numerador 5400 espaço kg espaço. espaço reto m ao quadrado dividido por reto s ao quadrado sobre denominador 2 espaço reto m fim da fração Fc igual a 2700 espaço tipográfico numerador kg. reto m sobre denominador reto s ao quadrado fim da fração igual a 2700 espaço reto N igual a 2 vírgula 7.10 ao cubo espaço reto N$

Existe força centrífuga?

Ao realizarmos uma curva em um automóvel, temos a impressão de que uma força nos puxa, “para fora da curva”. Essa sensação se dá pela inércia dos corpos, não por uma força.

A primeira Lei de Newton diz que um corpo tende a permanecer em velocidade constante (módulo, direção e sentido), a menos que outra força atue sobre o corpo. Esta propriedade dos corpos é chamada inércia.

Essa resistência a continuar o movimento, devido à inércia, é a causa da impressão de que uma força esteja resistindo à curva. No entanto, esta força não existe.

É a força centrípeta que atua alterando a trajetória original retilínea. Assim, afirmamos que só há força radial em trajetórias curvilíneas apontando para o centro da trajetória, nunca para fora.

Leia também sobre Força e Força de Atrito.

Exercícios de força centrípeta

Questão 1

Determine a força centrípeta descrita por uma montanha-russa com massa de 1000 kg e aceleração centrípeta de 200 m/s².

Ver Resposta

Resposta correta: 200.000 N

Utilizando a fórmula da Segunda Lei de Newton, temos:

$reto F com reto c subscrito espaço igual a espaço reto m espaço. espaço reto a com reto c subscrito espaço reto F com reto c espaço subscrito fim do subscrito igual a espaço 1000 espaço kg espaço. espaço 200 espaço reto m dividido por reto s à potência de 2 espaço fim do exponencial reto F com reto c subscrito espaço igual a espaço 200 espaço 000 espaço tipográfico numerador kg. reto m sobre denominador reto s ao quadrado fim da fração espaço igual a espaço 200 espaço 000 espaço reto N$

Logo, a força centrípeta é de 200 000 N ou 2.10⁵ N.

Questão 2

Na estrada, um caminhão descreve uma trajetória circular com aceleração centrípeta de 2 m/s². Sendo o raio da pista de 1800 m, calcule a velocidade do veículo.

Ver Resposta

Resposta correta: 60 m/s.

Utilizando a fórmula da aceleração centrípeta, podemos calcular a velocidade do veículo durante a trajetória circular:

$reto a com reto c subscrito espaço igual a espaço reto v ao quadrado sobre reto r espaço 2 espaço reto m dividido por reto s ao quadrado espaço igual a numerador reto v ao quadrado sobre denominador 1800 espaço reto m espaço fim da fração 2 espaço reto m dividido por reto s ao quadrado espaço.1800 espaço reto m espaço igual a espaço reto v ao quadrado espaço reto v ao quadrado espaço igual a espaço 3600 espaço reto m ao quadrado dividido por reto s ao quadrado espaço reto v espaço igual a espaço raiz quadrada de 3600 espaço reto m ao quadrado dividido por reto s ao quadrado espaço fim da raiz reto v espaço igual a espaço 60 espaço reto m dividido por reto s$

Portanto, a velocidade do caminhão na curva é de 60 m/s.

Para praticar mais: Exercício sobre força centrípeta (com gabarito explicado)

Expanda seus conhecimentos com a leitura dos artigos:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações