Força elétrica: o que é e como usar a fórmula

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

Força elétrica é a interação de atração ou repulsão gerada entre duas cargas devido à existência de um campo elétrico ao redor delas.

A capacidade de uma carga criar forças elétricas foi descoberta e estudada pelo físico francês Charles Augustin de Coulomb (1736-1806) no final do século XVIII.

Por volta de 1780, Coulomb criou a balança de torção e com esse instrumento demonstrou experimentalmente que a intensidade da força elétrica é diretamente proporcional ao valor das cargas elétricas que interagem e inversamente proporcional ao quadrado da distância que as separa.

Fórmula da força elétrica

A fórmula matemática, também chamada Lei de Coulomb, que expressa a intensidade da força elétrica é:

reto F espaço igual a reto K espaço numerador abre barra vertical reto q com 1 subscrito fecha barra vertical abre barra vertical reto q com 2 subscrito fecha barra vertical sobre denominador reto r ao quadrado fim da fração

Onde,

No Sistema Internacional de unidades (SI), a intensidade da força elétrica (F) é expressa em newton (N).

Os termos q1 e q2 da fórmula correspondem aos valores absolutos das cargas elétricas, cuja unidade no SI é coulomb (C), e a distância que separa as duas cargas (r) é representada em metros (m).

A constante de proporcionalidade (K) depende do meio que as cargas estão inseridas, por exemplo, no vácuo esse termo recebe o nome de constante eletrostática (K0) e seu valor é 9.109 N.m2/C2.

Saiba mais sobre a Lei de Coulomb.

Para que é usada a fórmula da força elétrica e como calcular?

A fórmula criada por Coulomb é utilizada para descrever a intensidade da interação mútua entre duas cargas puntiformes. Essas cargas são corpos eletrizados cujas dimensões são desprezíveis se comparadas com a distância entre elas.

A atração elétrica ocorre entre cargas que possuem sinais opostos, porque a força existente é de atração. A repulsão elétrica ocorre quando cargas de mesmo sinal são aproximadas, já que a força repulsiva atua sobre elas.

Error converting from MathML to accessible text.

Para calcular a força elétrica os sinais das cargas elétricas não são levados em consideração, apenas seus valores. Veja como calcular a força elétrica com os exemplos a seguir.

Exemplo 1
Duas partículas eletrizadas, q1 = 3,0 x 10-6 C e q2 = 5,0 x 10-6 C, e de dimensões desprezíveis situam-se a uma distância de 5 cm uma da outra. Determine a intensidade da força elétrica considerando que elas estão no vácuo. Utilize a constante eletrostática K0 = 9 . 109 N.m2/C2.

Resolução
Para encontrar a força elétrica, os dados devem ser aplicados na fórmula com as mesmas unidades da constante eletrostática.

Observe que a distância foi dada em centímetros, mas a constante apresenta metro e, por isso, o primeiro passo é transformar a unidade de distância.

1 espaço cm espaço igual a espaço 1 sobre 100 espaço reto m 5 espaço cm espaço igual a espaço 5 sobre 100 espaço reto m igual a 0 vírgula 05 espaço reto m

O próximo passo é substituir os valores na fórmula e calcular a força elétrica.

reto F espaço igual a reto K espaço numerador abre barra vertical reto q com 1 subscrito fecha barra vertical abre barra vertical reto q com 2 subscrito fecha barra vertical sobre denominador reto r ao quadrado fim da fração reto F espaço igual a espaço 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador parêntese esquerdo 3 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito espaço. espaço parêntese esquerdo 5 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito sobre denominador parêntese esquerdo 0 vírgula 05 espaço reto m parêntese direito ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador 15 vírgula 0 espaço reto x espaço 10 à potência de menos 6 mais parêntese esquerdo menos 6 parêntese direito fim do exponencial espaço reto C ao quadrado sobre denominador 0 vírgula 0025 espaço reto m ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. riscado diagonal para cima sobre reto m ao quadrado fim do riscado sobre denominador riscado diagonal para cima sobre reto C ao quadrado fim do riscado fim da fração. numerador 15 vírgula 0 espaço. espaço 10 à potência de menos 12 fim do exponencial espaço riscado diagonal para cima sobre reto C ao quadrado fim do riscado sobre denominador 0 vírgula 0025 espaço riscado diagonal para cima sobre reto m ao quadrado fim do riscado fim da fração reto F espaço igual a numerador 135 espaço sobre denominador 0 vírgula 0025 fim da fração espaço.10 à potência de 9 mais parêntese esquerdo menos 12 parêntese direito fim do exponencial reto N reto F espaço igual a 54000 espaço. espaço 10 à potência de menos 3 fim do exponencial espaço reto N reto F espaço igual a 54 espaço reto N

Chegamos a conclusão que a intensidade da força elétrica que age sobre as cargas é de 54 N.

Você também pode se interessar por Eletrostática.

Exemplo 2
A distância entre os pontos A e B é de 0,4 m e nas extremidades estão situadas as cargas Q1 e Q2. Uma terceira carga, Q3, foi inserida em um ponto que está a 0,1 m de Q1.

Error converting from MathML to accessible text.

Calcule a força resultante sobre Q3 sabendo que:

  • Q1 = 2,0 x 10-6 C
  • Q2 = 8,0 x 10-6 C
  • Q3 = – 3,0 x 10-6 C
  • K0 = 9 . 109 N.m2/C2

Resolução
O primeiro passo para resolver esse exemplo é calcular a intensidade da força elétrica entre duas cargas por vez.

Vamos iniciar calculando a força de atração entre Q1 e Q3.

reto F espaço igual a reto K com 0 subscrito espaço numerador abre barra vertical reto q com 1 subscrito fecha barra vertical abre barra vertical reto q com 3 subscrito fecha barra vertical sobre denominador reto d com 1 subscrito ao quadrado fim da fração reto F espaço igual a espaço 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador parêntese esquerdo 2 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito espaço. espaço parêntese esquerdo 3 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito sobre denominador parêntese esquerdo 0 vírgula 1 espaço reto m parêntese direito ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador 6 vírgula 0 espaço reto x espaço 10 à potência de menos 6 mais parêntese esquerdo menos 6 parêntese direito fim do exponencial espaço reto C ao quadrado sobre denominador 0 vírgula 01 espaço reto m ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. riscado diagonal para cima sobre reto m ao quadrado fim do riscado sobre denominador riscado diagonal para cima sobre reto C ao quadrado fim do riscado fim da fração. numerador 6 vírgula 0 espaço. espaço 10 à potência de menos 12 fim do exponencial espaço riscado diagonal para cima sobre reto C ao quadrado fim do riscado sobre denominador 0 vírgula 01 espaço riscado diagonal para cima sobre reto m ao quadrado fim do riscado fim da fração reto F espaço igual a numerador 54 espaço sobre denominador 0 vírgula 01 fim da fração espaço.10 à potência de 9 mais parêntese esquerdo menos 12 parêntese direito fim do exponencial reto N reto F espaço igual a 5400 espaço. espaço 10 à potência de menos 3 fim do exponencial espaço reto N reto F espaço igual a 5 vírgula 4 espaço reto N

Agora, calculamos a força de atração entre Q3 e Q2.

Se a distância total entre a reta AB com barra sobrescrito é de 0,4 m e Q3 está posicionada a 0,1 m de A, quer dizer que a distância entre Q3 e Q2 é de 0,3 m.

reto F espaço igual a reto K com 0 subscrito espaço numerador abre barra vertical reto q com 3 subscrito fecha barra vertical abre barra vertical reto q com 2 subscrito fecha barra vertical sobre denominador reto d com 2 subscrito ao quadrado fim da fração reto F espaço igual a espaço 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador parêntese esquerdo 3 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito espaço. espaço parêntese esquerdo 8 vírgula 0 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço reto C parêntese direito sobre denominador parêntese esquerdo 0 vírgula 3 espaço reto m parêntese direito ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. reto m ao quadrado sobre denominador reto C ao quadrado fim da fração. numerador 24 vírgula 0 espaço reto x espaço 10 à potência de menos 6 mais parêntese esquerdo menos 6 parêntese direito fim do exponencial espaço reto C ao quadrado sobre denominador 0 vírgula 09 espaço reto m ao quadrado fim da fração reto F espaço igual a 9 espaço. espaço 10 à potência de 9 espaço numerador reto N. riscado diagonal para cima sobre reto m ao quadrado fim do riscado sobre denominador riscado diagonal para cima sobre reto C ao quadrado fim do riscado fim da fração. numerador 24 vírgula 0 espaço. espaço 10 à potência de menos 12 fim do exponencial espaço riscado diagonal para cima sobre reto C ao quadrado fim do riscado sobre denominador 0 vírgula 09 espaço riscado diagonal para cima sobre reto m ao quadrado fim do riscado fim da fração reto F espaço igual a numerador 216 sobre denominador 0 vírgula 09 fim da fração espaço.10 à potência de 9 mais parêntese esquerdo menos 12 parêntese direito fim do exponencial reto N reto F espaço igual a 2400 espaço. espaço 10 à potência de menos 3 fim do exponencial espaço reto N reto F espaço igual a 2 vírgula 4 espaço reto N

A partir dos valores das forças de atração entre as cargas, podemos calcular a força resultante da seguinte forma:

reto F com reto r subscrito espaço igual a espaço reto F com 13 subscrito espaço menos espaço reto F com 23 subscrito reto F com reto r subscrito espaço igual a espaço 5 vírgula 4 espaço reto N espaço menos espaço 2 vírgula 4 espaço reto N reto F com reto r subscrito espaço igual a espaço 3 espaço reto N

Chegamos a conclusão que a força elétrica resultante que Q1 e Q2 exercem sobre Q3 é de 3 N.

Exercícios de Força elétrica

Exercício 1

(PUC - RS 2016) Três esferas de dimensões desprezíveis A, B e C estão eletricamente carregadas com cargas elétricas respectivamente iguais a 2q, q e q. Todas encontram-se fixas, apoiadas em suportes isolantes e alinhadas horizontalmente, como mostra a figura abaixo:

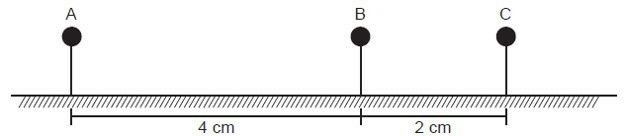
Imagem associada à questão.

O módulo da força elétrica exercida por B na esfera C é F. O módulo da força elétrica exercida por A na esfera B é

a) F/4

b) F/2

c) F

2F

4F

Gabarito explicado

O módulo da força elétrica é dado por:

F igual a numerador K. q 1. q 2 sobre denominador r ao quadrado fim da fração

De B para C

F com B C subscrito fim do subscrito igual a F igual a numerador K. q. q sobre denominador 2 ao quadrado fim da fração igual a numerador K q ao quadrado sobre denominador 4 fim da fração

De A para B

F com A B subscrito fim do subscrito igual a numerador K.2 q. q sobre denominador 4 ao quadrado fim da fração igual a numerador 2 K q ao quadrado sobre denominador 16 fim da fração igual a numerador K q ao quadrado sobre denominador 8 fim da fração

Assim F com A B subscrito fim do subscrito igual a F sobre 2 pois,

F com A B subscrito fim do subscrito igual a F sobre 2numerador K q ao quadrado sobre denominador 8 fim da fração igual a numerador começar estilo mostrar numerador K q ao quadrado sobre denominador 4 fim da fração fim do estilo sobre denominador 2 fim da fraçãonumerador K q ao quadrado sobre denominador 8 fim da fração igual a numerador K q ao quadrado sobre denominador 4 fim da fração.1 meio igual a numerador K q ao quadrado sobre denominador 8 fim da fração

Exercício 2

(UNIFESP-SP) Duas partículas de cargas elétricas estão separadas no vácuo por uma distância de 3 vírgula 0 espaço. espaço 10 à potência de menos 9 fim do exponencialm. Sendo k igual a 9 vírgula 0 espaço. espaço 10 à potência de 9 espaço N. m ao quadrado dividido por C ao quadrado, a intensidade da força de interação entre elas, em newtons, é de

(UNIFESP-SP) Duas partículas de cargas elétricas q com 1 subscrito igual a 4 vírgula 0 espaço. espaço 10 à potência de menos 16 fim do exponencial C espaço e q com 2 subscrito igual a 6 vírgula 0 espaço. espaço 10 à potência de menos 16 fim do exponencial Cestão separadas no vácuo por uma distância de 3 vírgula 0 espaço. espaço 10 à potência de menos 9 fim do exponencialm. Sendok igual a 9 vírgula 0 espaço. espaço 10 à potência de 9 espaço fim do exponencial N. m ao quadrado dividido por C ao quadrado, a intensidade da força de interação entre elas, em newtons, é de

1 vírgula 2 espaço. espaço 10 à potência de menos 5 fim do exponencial.

1 vírgula 8 espaço. espaço 10 à potência de menos 4 fim do exponencial.

2 vírgula 0 espaço. espaço 10 à potência de menos 4 fim do exponencial.

2 vírgula 4 espaço. espaço 10 à potência de menos 4 fim do exponencial.

3 vírgula 0 espaço. espaço 10 à potência de menos 3 fim do exponencial.

Gabarito explicado

A intensidade ou módulo da força elétrica de interação eletrostática é dado pela aplicação da Lei de Coulomb:

F igual a numerador k. q com 1 subscrito. q com 2 subscrito sobre denominador r ao quadrado fim da fração

Substituindo os valores fornecidos:

F igual a numerador 9 vírgula 0 sinal de multiplicação 10 à potência de 9. espaço 4 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial. espaço 6 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial sobre denominador parêntese esquerdo 3 vírgula 0 sinal de multiplicação 10 à potência de menos 9 fim do exponencial parêntese direito ao quadrado fim da fraçãoF igual a numerador 9 vírgula 0 sinal de multiplicação 10 à potência de 9. espaço 4 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial. espaço 6 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial sobre denominador 9 vírgula 0 sinal de multiplicação 10 à potência de menos 18 fim do exponencial fim da fraçãoF igual a numerador 9 vírgula 0 sinal de multiplicação 10 à potência de 9. espaço 4 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial. espaço 6 vírgula 0 sinal de multiplicação 10 à potência de menos 16 fim do exponencial sobre denominador 9 vírgula 0 sinal de multiplicação 10 à potência de menos 18 fim do exponencial fim da fraçãoF igual a numerador 216 sinal de multiplicação 10 à potência de 9 mais parêntese esquerdo menos 16 parêntese direito mais parêntese esquerdo menos 16 parêntese direito fim do exponencial sobre denominador 9 vírgula 0 sinal de multiplicação 10 à potência de menos 18 fim do exponencial fim da fraçãoF igual a numerador 216 sinal de multiplicação 10 à potência de menos 23 fim do exponencial sobre denominador 9 vírgula 0 sinal de multiplicação 10 à potência de menos 18 fim do exponencial fim da fraçãoF igual a 24 sinal de multiplicação 10 à potência de menos 23 menos parêntese esquerdo menos 18 parêntese direito fim do exponencialF igual a 24 sinal de multiplicação 10 à potência de menos 23 mais 18 fim do exponencialF igual a 24 sinal de multiplicação 10 à potência de menos 5 fim do exponencial

Em notação científica:

F igual a 2 vírgula 4 sinal de multiplicação 10 à potência de menos 4 fim do exponencial espaço N

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também