Fração Geratriz

Rosimar Gouveia

Professora de Matemática e Física

Adicionar aos favoritos Salvar Adicionar aos favoritos

Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico).

Os números decimais periódicos apresentam um ou mais algarismos que se repetem infinitamente. Esse algarismo ou algarismos que se repetem representam o período do número.

Quando o parte decimal é composta apenas pelo período, a dizima é classificada como simples. Já quando além do período existir, na parte decimal, algarismos que não se repetem, a dízima será composta.

Exemplos

Cálculo da fração geratriz

Encontrar a fração geratriz de uma dízima periódica muitas vezes é necessário para que possamos efetuar cálculos, por exemplo, em expressões numéricas.

Para descobrir a fração geratriz de uma dízima periódica simples, podemos seguir os seguintes passos:

• 1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.
• 2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos "andar" para que o período fique antes da vírgula.
• 3º passo: Diminuir a equação encontrada da equação inicial.
• 4º passo: Isolar a incógnita.

Saiba mais sobre as Expressões Numéricas.

Exemplos

1) Encontre a fração geratriz do número 0,8888...

Solução

Primeiro vamos escrever a equação do 1º grau, igualando o número a x:

x = 0,8888...

Observe que o período é composto por um único algarismo (8). Assim sendo, temos que "andar" apenas uma casa para ter o período na frente da vírgula. Assim, multiplicaremos a equação por 10.

10 x = 10 . 0,8888...
10 x = 8,888...

Agora vamos diminuir as duas equações, ou seja:

Isolando o x, encontramos a fração geratriz:

Veja também: O que é Fração?

2) Transforme o número decimal 0,454545... em fração.

Solução

Iremos seguir os mesmos passos do exemplo anterior. A única diferença é que agora o período é composto de 2 algarismos (45). Neste caso, teremos que "andar" duas casas, e então iremos multiplicar por 100.

x = 0,454545...
100 x = 100 . 0,454545...
100 x = 45,454545...

Subtraindo as equações:

Isolando o x, descobrimos que a fração geratriz é igual a . Podemos ainda simplificar esta fração dividindo o numerador e o denominador por 9.

Assim, temos:

Quando a dízima periódica for composta, além dos passos indicados para a simples, devemos também multiplicar a primeira equação por um número múltiplo de 10, que a transforme em uma dízima simples.

Acompanhe o exemplo abaixo:

Qual a fração geratriz de 2,3616161...?

Veja também: Tipos de Frações

Solução

Neste exemplo, a dízima periódica é composta, pois o algarismo 3, que aparece depois da vírgula, não se repete.

Escrevendo a equação inicial, temos:

x = 2,3616161...

Como a dízima é composta, devemos primeiro multiplicar essa equação por 10, pois com isso, passamos o 3 para a frente da vírgula (algarismo que não se repete).

10 x = 23,616161...

Agora vamos escrever a outra equação multiplicando ambos os lados da equação inicial por 1000, pois assim, conseguimos passar o período para a frente da vírgula.

1000 x = 2361,616161...

Em seguida, faremos a subtração dessas duas equações e isolaremos o x para encontrar a fração geratriz.

Veja também: Números Racionais

Método Prático

Para encontrar a fração geratriz de uma dízima periódica, podemos também utilizar um método prático.

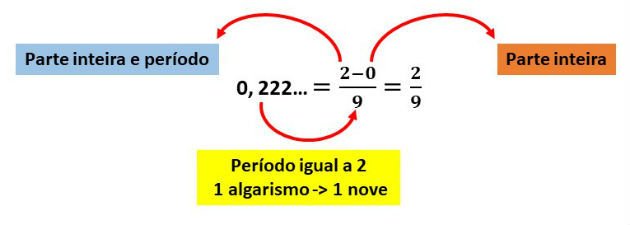
Quando a dízima for simples, o numerador será igual a parte inteira com o período menos a parte inteira, e no denominador, a quantidades de "noves" igual ao número de algarismo do período.

Exemplos

1) Determine a fração geratriz da dízima periódica 0,222...

Solução

Para encontrar a fração geratriz, vamos usar o método prático conforme esquematizado abaixo:

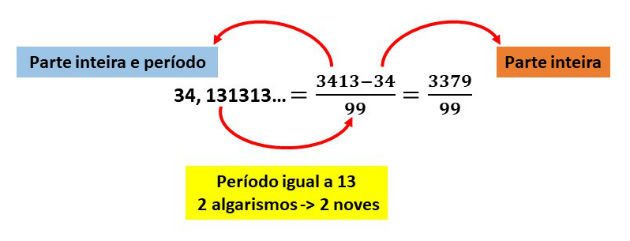
2) Qual a fração geratriz da dízima periódica 34,131313...?

Solução

Acompanhe o esquema abaixo para encontrar a fração geratriz.

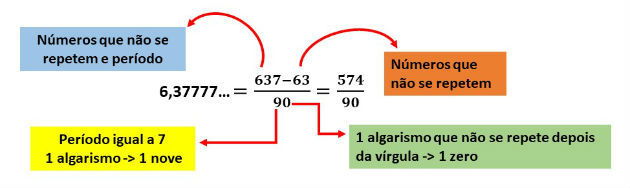
Quando a dízima for composta, o numerador será igual a parte que não se repete com o período, menos a parte que não se repete.

Exemplo

Encontre a fração geratriz da dízima periódica 6,3777...

Solução

Como a dízima periódica é composta, encontraremos a fração geratriz utilizando o seguinte esquema:

Exercícios Resolvidos

1) IFRS - 2017

Um menino estava na aula de matemática e a professora propôs uma atividade com fichas. Cada ficha tinha um número e a regra era colocar as fichas em ordem crescente. Observe a resolução do menino e determine V para verdadeiro e F para falso a cada sentença abaixo.

I - A resolução do menino, representada nas fichas acima, está correta.
II - Os números 1,333 … e – 0,8222... são dízimas periódicas.
III - O número decimal 1,333 … não pode ser escrito na forma .
IV - Adicionando apenas os valores positivos das fichas, obtemos .

Assinale a alternativa correta.

a) F – V – F – V
b) F – F – F – F
c) F – V – V – V
d) V – F – V – F
e) V – V –V – V

2) Colégio Naval - 2013

Qual é o valor da expressão

a) 0,3
b)
c) 1
d) 0
e) -1

Pratique mais Exercícios sobre fração geratriz e dízima periódica.

Para saber mais, veja também:

• Frações Equivalentes
• Adição e Subtração de Frações
• Multiplicação e Divisão de Frações
• Exercícios sobre divisão e multiplicação de frações

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.