Função Exponencial

Rosimar Gouveia

Professora de Matemática e Física

Função Exponencial é aquela que a variável está no expoente e cuja base é sempre maior que zero e diferente de um.

Essas restrições são necessárias, pois 1 elevado a qualquer número resulta em 1. Assim, em vez de exponencial, estaríamos diante de uma função constante.

Além disso, a base não pode ser negativa, nem igual a zero, pois para alguns expoentes a função não estaria definida.

Por exemplo, a base igual a - 3 e o expoente igual a 1/2. Como no conjunto dos números reais não existe raiz quadrada de número negativo, não existiria imagem da função para esse valor.

Exemplos:

f(x) = 4^x
f(x) = (0,1)^x
f(x) = (⅔)^x

Nos exemplos acima 4, 0,1 e ⅔ são as bases, enquanto x é o expoente.

Gráfico da função exponencial

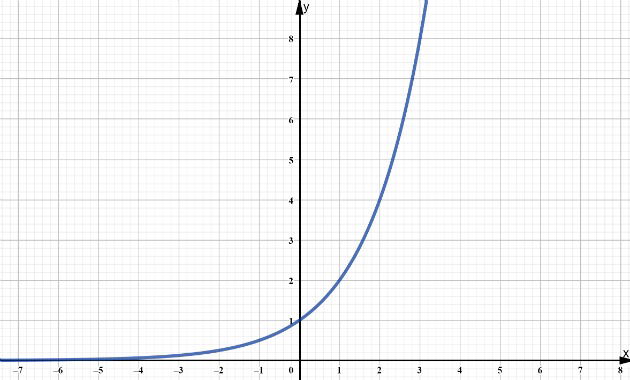
O gráfico desta função passa pelo ponto (0,1), pois todo número elevado a zero é igual a 1. Além disso, a curva exponencial não toca no eixo x.

Na função exponencial a base é sempre maior que zero, portanto a função terá sempre imagem positiva. Assim sendo, não apresenta pontos nos quadrantes III e IV (imagem negativa).

Abaixo representamos o gráfico da função exponencial.

Função Crescente ou Decrescente

A função exponencial pode ser crescente ou decrescente.

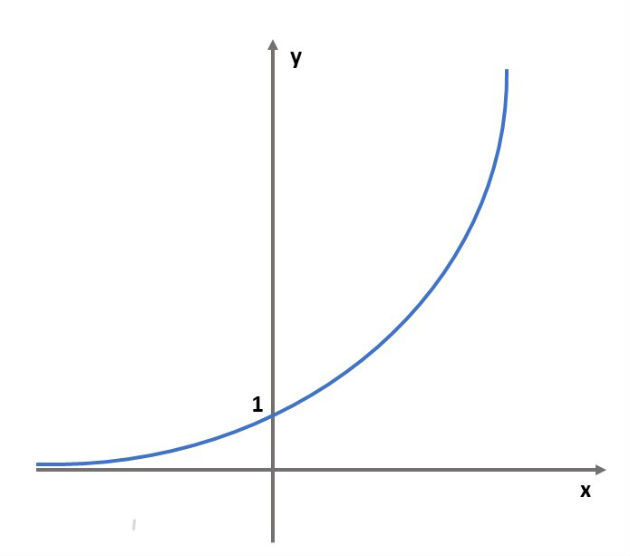
Será crescente quando a base for maior que 1. Por exemplo, a função y = 2^x é uma função crescente.

Para constatar que essa função é crescente, atribuímos valores para x no expoente da função e encontramos a sua imagem. Os valores encontrados estão na tabela abaixo.

Observando a tabela, notamos que quando aumentamos o valor de x, a sua imagem também aumenta. Abaixo, representamos o gráfico desta função.

Por sua vez, as funções cujas bases são valores maiores que zero e menores que 1, são decrescentes. Por exemplo, f(x) = (1/2)^x é uma função decrescente.

Calculamos a imagem de alguns valores de x e o resultado encontra-se na tabela abaixo.

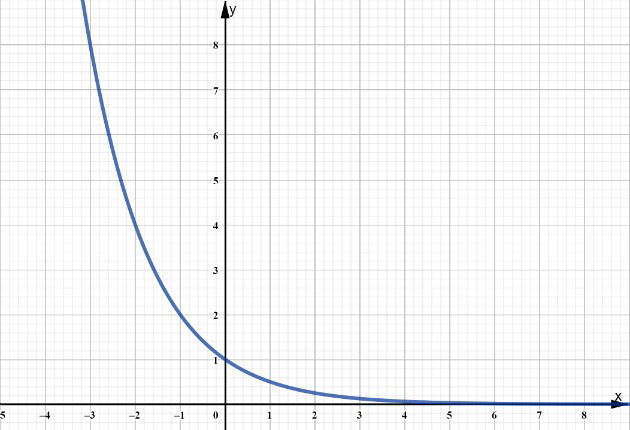
Notamos que para esta função, enquanto os valores de x aumentam, os valores das respectivas imagens diminuem. Desta forma, constatamos que a função f(x) = (1/2)^x é uma função decrescente.

Com os valores encontrados na tabela, traçamos o gráfico dessa função. Note que quanto maior o x, mais perto do zero a curva exponencial fica.

Função Logarítmica

A inversa da função exponencial é a função logarítmica. A função logarítmica é definida como f(x) = log_ax, com a real positivo e a ≠ 1.

Sendo, o logaritmo de um número definido como o expoente ao qual se deve elevar a base a para obter o número x, ou seja, y = log_ax ⇔ a^y = x.

Uma relação importante é que o gráfico de duas funções inversas são simétricos em relação a bissetriz dos quadrantes I e III.

Desta maneira, conhecendo o gráfico da função exponencial de mesma base, por simetria podemos construir o gráfico da função logarítmica.

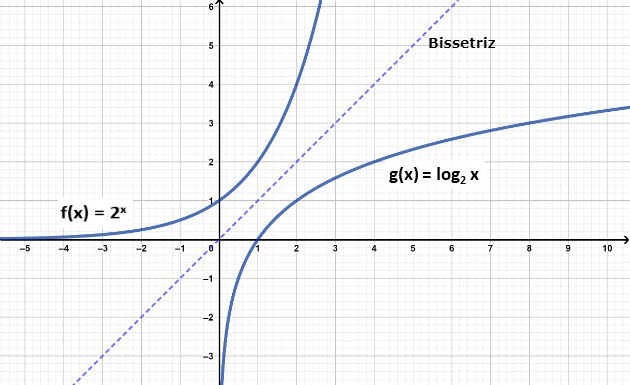
No gráfico acima, observamos que enquanto a função exponencial cresce rapidamente, a função logarítmica cresce lentamente.

Leia também:

• Função Exponencial - Exercícios
• Equação exponencial
• Exercícios de equação exponencial
• O que é função
• Potenciação
• Exercícios de Potenciação
• Logaritmo - Exercícios
• Propriedades dos Logaritmos
• Função Afim
• Função Quadrática
• Função Quadrática - Exercícios
• Função Modular
• Exercícios sobre função modular
• Função Composta
• Função Inversa
• Função Injetora
• Função Bijetora
• Função Sobrejetora
• Funções Trigonométricas
• Fórmulas de Matemática

Exercícios de Vestibular Resolvidos

1. (Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v₀ . 2 ^-0,2t, em que v₀ é uma constante real.

Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.

2. (PUCC-SP) Numa certa cidade, o número de habitantes, num raio de r km a partir do seu centro é dado por P(r) = k . 2^3r, em que k é constante e r > 0.

Se há 98 304 habitantes num raio de 5 km do centro, quantos habitantes há num raio de 3 km do centro?

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.