Função modular: entenda o que é e como calcular (com exemplos)

Rafael C. Asth

Professor de Matemática e Física

Função modular é a função (lei ou regra) que associa elementos de um conjunto em módulos.

O módulo é representado entre barras e retorna sempre um número positivo. A função modular é usada para calcular a distância entre um número e zero, ignorando o sinal.

Também chamada de função módulo ou função valor absoluto, é expressa como:

Se , a função retorna o valor x.

Exemplo

Se , a função retorna o valor - x.

Exemplo

Embora esta seja a forma mais simples da função modular, ela pode ser combinada com outras operações, por exemplo:

Esta função, associa elementos do domínio ao contradomínio . Isto significa que a função aceita qualquer valor do conjunto dos números reais e retorna, também, valores do conjunto dos números reais. Matematicamente escrevemos: .

Como esboçar o gráfico de uma função modular

O gráfico de uma função é a representação de seus pares ordenados (x, y) em um plano cartesiano. Para esboçá-lo, vamos analisar por partes.

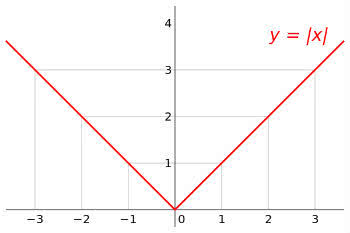
Gráfico da função .

Fazendo uma tabela para alguns valores:

Ao colocarmos estes valores no plano cartesiano, obtemos:

A função modular possui duas seções, uma descendente f(-x) = - x para x < 0 e, uma ascendente f(x) = x para x 0.

Ao representar um módulo negativo, o gráfico para na intersecção e volta a fazer o sentido ascendente.

Isso porque tudo o que fica abaixo tem valor negativo e os módulos negativos sempre se tornam números positivos.

Propriedades dos módulos

Existem algumas propriedades (algumas regras) que ajudam e simplificam cálculos. Aqui estão:

1. Todo x ∊ R, temos |x| = |-x|
2. Todo x ∊ R, temos |x²| = |x|²= x²
3. Todo x e y ∊ R, temos |x.y| = |x| . |y|
4. Todo x e y ∊ R, temos |x + y| ≤ |x| + |y|

Repare que os números reais são o domínio de cada uma das funções acima.

Leia também sobre o que é função?

Exercícios sobre função modular

Exercício 1

(UNITAU) O domínio da função f(x) = √ [(1-|x-1|)/2] é:

a) 0 ≤ x ≤ 2.
b) x ≥ 2.
c) x ≤ 0.
d) x < 0.
e) x > 0.

Exercício 2

(UFG) Relativamente à função f, de R em R, dada por f(x)=|x|+|x-1|, é correto afirmar que

a) o gráfico de f é a reunião de duas semirretas.
b) o conjunto imagem de f é o intervalo [1, + ∞].
c) f é crescente para todo x ∊ R.
d) f é decrescente para todo x ∊ R. e x ≥ 0.
e) o valor mínimo de f é 0.

Exercício 3

(UFG) Seja R o conjunto dos números reais. Considere a função f:R→R, definida por f(x)=|1-|x||.

Assim,

( ) f(-4) = 5.
( ) o valor mínimo de f é zero.
( ) f é crescente para x no intervalo [0,1].
( ) a equação f(x) = 1 possui três soluções reais distintas.

Pratique com exercícios de função modular.

Conheça outros tipos de funções:

• Função Quadrática
• Função Exponencial
• Função Composta
• Função Afim

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.