Função par e função ímpar

Rafael C. Asth

Professor de Matemática e Física

Uma função matemática pode ser classificada como par ou ímpar, dependendo de algumas características. Também conhecida como paridade, indica se são simétricas em relação ao eixo y ou à origem de um sistema cartesiano.

As funções são expressões que recebem valores x e os transformam em valores y, seguindo as operações em sua lei de formação. Conforme este conjunto de pares ordenados (x, y) são pontuados em um plano cartesiano, formam um gráfico.

Funções pares produzem gráficos simétricos ao eixo y e funções ímpares simétricas à origem do sistema cartesiano.

Uma função sem paridade é que não possui nenhuma destas características, ou seja, não é par nem ímpar.

Função ímpar

Uma função é ímpar quando f(-x) = -f(x). Isto significa que os valores assumidos pela função serão simétricos tanto em relação ao eixo x, quanto em relação ao eixo y.

Exemplo
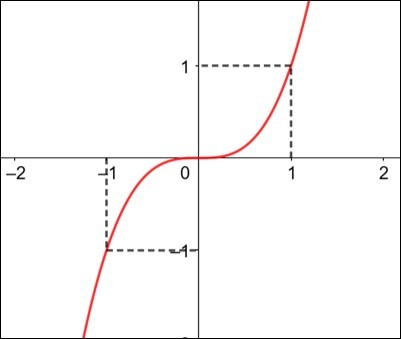
Função f:R→R definida por .

x	f(x)	y
-1		-1
0		0
1		1

Verificamos que f(-1) = -f(1) = -1, portanto a função é ímpar e seu gráfico é simétrico em relação à origem.

Função par

Uma função é par quando f(-x) = f(x). Isto significa que o valor assumido pela função nos pontos x e -x são iguais. Desta forma, podemos dizer que a função assume valores iguais para valores de x simétricos.

Exemplo
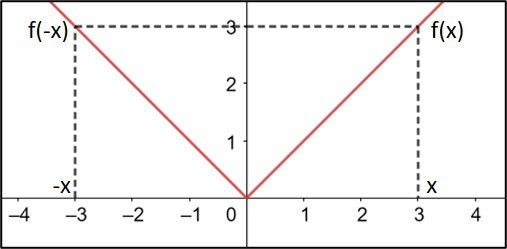
Função f:R→R definida por .

x	f(x)	y
-3		3
0		0
3		3

Verificamos que f(-3) = f(3) = 3, de forma que a função é par e seu gráfico é simétrico em relação ao eixo y.

Aprenda mais sobre funções.

Talvez se interesse por:

• Domínio, contradomínio e imagem
• Função Sobrejetora
• Função Bijetora
• Função Injetora
• Função Inversa
• Função Composta

Pratique também exercícios sobre domínio, contradomínio e imagem.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.