Função quadrática

A função quadrática, também chamada de função polinomial de 2º grau, é uma função representada pela seguinte expressão:

f(x) = ax² + bx + c

Onde a, b e c são números reais e a ≠ 0.

Exemplo:

f(x) = 2x² + 3x + 5,

sendo,

a = 2
b = 3
c = 5

Nesse caso, o polinômio da função quadrática é de grau 2, por ser o maior expoente da variável x.

O conjunto domínio das funções quadráticas são os números reais, assim como seu contradomínio (). Já o conjunto imagem depende do vértice da parábola e de sua concavidade.

Gráfico da função quadrática: a parábola

O gráfico das funções do 2º grau são curvas que recebem o nome de parábolas. Diferente das funções do 1º grau, onde conhecendo dois pontos é possível traçar o gráfico, nas funções quadráticas são necessários conhecer vários pontos.

A curva de uma função quadrática corta o eixo x nas raízes ou zeros da função, em no máximo dois pontos dependendo do valor do discriminante (Δ). Assim, temos:

• Se Δ > 0, o gráfico cortará o eixo x em dois pontos;
• Se Δ < 0, o gráfico não cortará o eixo x;
• Se Δ = 0, a parábola tocará o eixo x em apenas um ponto.

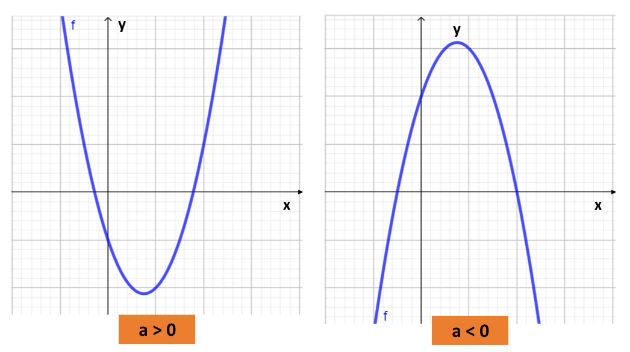
Relação entre a parábola e os parâmetros a, b e c

É possível identificar a posição da concavidade da curva analisando apenas o sinal do coeficiente a. Se o coeficiente for positivo, a concavidade ficará voltada para cima e se for negativo ficará para baixo.

O parâmetro b indica se a parábola corta o eixo y no ramo descendente ou ascendente. Caso o b seja negativo, a parábola cruza o eixo y na "descida", como na parábola da esquerda da imagem anterior. Já se o b for positivo, a parábola cruza o eixo y na "subida", como na parábola da direita da imagem anterior.

O parâmetro c indica exatamente a ordenada do ponto onde a parábola cruza o eixo y. Ou seja, ele indica o valor do y no ponto onde a parábola corta seu eixo.

Exemplo da parábola da função f(x) = 2x² + 3x + 5.

• a = 2
• b = 3
• c =5

Sendo a um valor positivo, a parábola tem concavidade para cima.

O parâmetro b também é positivo, logo a parábola cortará o eixo y na subida.

Ainda, a parábola irá cortar o eixo y na ordenada 5.

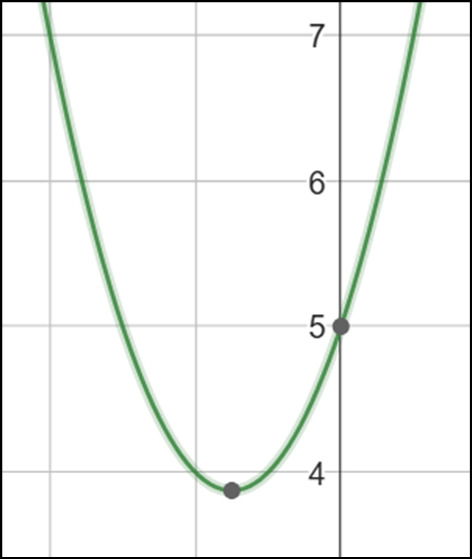
Como a parábola não cruza o eixo x, esse é um caso em que Δ < 0.

A partir dos pares ordenados dados (x, y), podemos construir a parábola num plano cartesiano, por meio da ligação entre os pontos encontrados.

Aprenda mais sobre:

• Funções do 1º grau
• Vértice da parábola

Raízes da Função

As raízes ou zeros da função do segundo grau representam aos valores de x tais que f(x) = 0. As raízes da função são determinadas pela resolução da equação de segundo grau, bastante fazer f(x) = 0.

0 = ax² +bx + c

Para resolver a equação do 2º grau podemos utilizar vários métodos, sendo um dos mais utilizados é aplicando a Fórmula de Bhaskara, ou seja:

Exemplo de cálculo das raízes da função f(x) = x² – 5x + 6.

Resolução:

Sendo
a = 1
b = – 5
c = 6

Substituindo esses valores na fórmula de Bhaskara, temos:

Portanto, as raízes são 2 e 3.

Vértice da parábola: as coordenadas do extremo

Existe ainda outro ponto, chamado de vértice da parábola, sendo o valor máximo ou mínimo da função. Este ponto é encontrado usando-se a seguinte fórmula:

O vértice irá representar o ponto de valor máximo da função quando a parábola estiver voltada para baixo e o valor mínimo quando estiver para cima.

Exemplo de cálculo do vértice da função f(x) = x² – 5x + 6.

Substituindo os valores:

Como determinar uma função quadrática

Determinar a lei de formação de uma função é conhecer o valor numérico de seus parâmetros. No caso da função quadrática, os valores de a, b e c.

Confira abaixo o passo a passopor meio um exemplo de resolução da função quadrática:

Determine a, b e c na função quadrática dada por: f(x) = ax² + bx + c, sendo:

f (-1) = 8
f (0) = 4
f (2) = 2

Primeiramente, vamos substituir o x pelos valores de cada função e assim teremos:

f (-1) = 8
a (-1)² + b (–1) + c = 8
a - b + c = 8 (equação I)

f (0) = 4
a . 0² + b . 0 + c = 4
c = 4 (equação II)

f (2) = 2
a . 2² + b . 2 + c = 2
4a + 2b + c = 2 (equação III)

Pela segunda função f (0) = 4, já temos o valor de c = 4.

Assim, vamos substituir o valor obtido para c nas equações I e III para determinar as outras incógnitas (a e b):

(Equação I)

a - b + 4 = 8
a - b = 4
a = b + 4

Já que temos a equação de a pela Equação I, vamos substituir na III para determinar o valor de b:

(Equação III)

4a + 2b + 4 = 2
4a + 2b = - 2
4 (b + 4) + 2b = - 2
4b + 16 + 2b = - 2
6b = - 18
b = - 3

Por fim, para encontrar o valor de a substituímos os valores de b e c que já foram encontrados. Logo:

(Equação I)

a - b + c = 8
a - (- 3) + 4 = 8
a = - 3 + 4
a = 1

Sendo assim, os coeficientes da função quadrática dada são:

a = 1
b = - 3
c = 4

Exercícios sobre função quadrática

Exercício 1

(Vunesp-SP) Todos os possíveis valores de m que satisfazem a desigualdade 2x² – 20x – 2m > 0, para todo x pertencente ao conjunto dos reais, são dados por:

a) m > 10
b) m > 25
c) m > 30
d) m
e) m

Exercício 2

(UE-CE) O gráfico da função quadrática f(x) = ax² + bx é uma parábola cujo vértice é o ponto (1, – 2). O número de elementos do conjunto x = {(– 2, 12), (–1,6), (3,8), (4, 16)} que pertencem ao gráfico dessa função é:

a) 1
b) 2
c) 3
d) 4

Exercício 3

(Cefet-SP) Sabendo que as equações de um sistema são x . y = 50 e x + y = 15, os possíveis valores para x e y são:

a) {(5,15), (10,5)}
b) {(10,5), (10,5)}
c) {(5,10), (15,5)}
d) {(5,10), (5,10)}
e) {(5,10), (10,5)}

Leia também:

• Equação do Segundo Grau
• Exercícios de Função Afim
• Equação do 2º Grau - Exercícios
• Soma e produto
• Função Injetora
• Função Bijetora
• Função Quadrática - Exercícios
• Matemática no Enem
• Fórmulas de Matemática