Geometria analítica

Rafael C. Asth

Professor de Matemática e Física

A Geometria Analítica estuda elementos geométricos em um sistema de coordenadas num plano ou espaço. Estes objetos geométricos são determinados por sua localização e posição em relação a pontos e eixos deste sistema de orientação.

Desde povos da antiguidade, como egípcios e romanos, a ideia de coordenadas já aparece na história. Mas é no século XVII, com os trabalhos de René Descartes e Pierre de Fermat que este campo da Matemática se sistematiza.

Sistema cartesiano ortogonal

O Sistema Cartesiano Ortogonal é uma base de referência para localização de coordenadas. É constituído, em um plano, por dois eixos perpendiculares entre si.

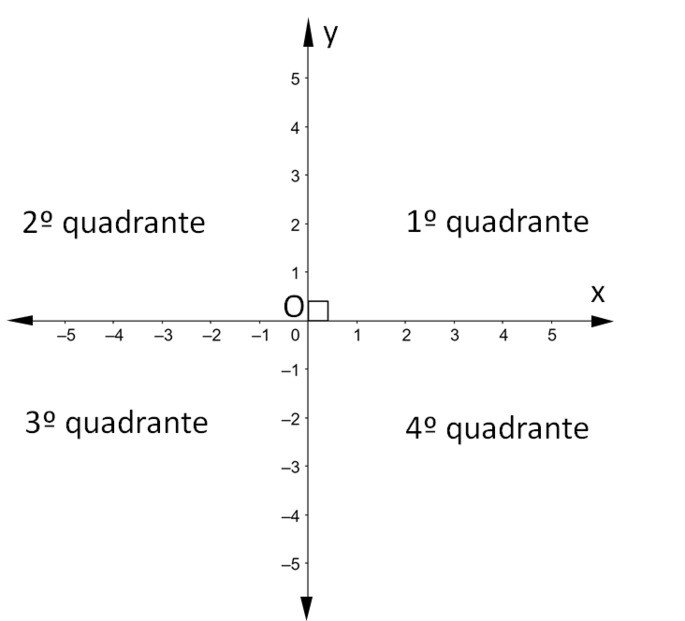
Sistema Cartesiano Ortogonal

A origem O(0,0) deste sistema é a intersecção destes eixos.
O eixo x é o das abscissas.
O eixo y é o das ordenadas.
Convenciona-se a orientação anti-horária dos quatro quadrantes.

Par ordenado

Um ponto qualquer no plano possui a coordenada P(x, y).

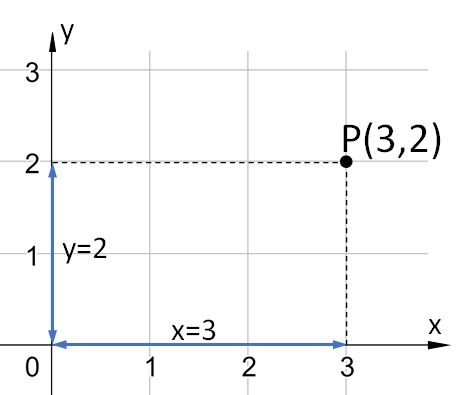
x é a abscissa do ponto P e constitui a distância entre sua projeção ortogonal no eixo x até a origem.
y é a ordenada do ponto P e constitui a distância entre sua projeção ortogonal no eixo y até a origem.

Distância entre dois pontos

A distância entre dois pontos no plano cartesiano é o comprimento do segmento que une estes dois pontos.

Fórmula da distância entre dois pontos $reto A parêntese esquerdo reto x com reto A subscrito vírgula espaço reto y com reto A subscrito parêntese direito$ e $reto B abre parênteses reto x com reto B subscrito vírgula espaço reto y com reto B subscrito espaço fecha parênteses$ quaisquer.

$começar estilo tamanho matemático 22px reto d com AB subscrito igual a raiz quadrada de parêntese esquerdo reto x com reto B subscrito menos reto x com reto A subscrito parêntese direito ao quadrado mais parêntese esquerdo reto y com reto B subscrito menos reto y com reto A subscrito parêntese direito ao quadrado fim da raiz fim do estilo$

Coordenadas do ponto médio

Ponto médio é o ponto que divide um segmento em duas partes de mesma medida.

Sendo $M abre parênteses x com M subscrito vírgula espaço y com M subscrito fecha parênteses$ o ponto médio de um segmento $pilha A B com barra acima$ , suas coordenadas são as médias aritméticas das abscissas e ordenadas.

$começar estilo tamanho matemático 22px x com reto M subscrito igual a numerador reto x com reto B subscrito mais reto x com reto A subscrito sobre denominador 2 fim da fração fim do estilo$ e $começar estilo tamanho matemático 22px reto y com reto M subscrito igual a numerador reto y com reto B subscrito mais reto y com reto A subscrito sobre denominador 2 fim da fração fim do estilo$

Condição de alinhamento de três pontos

Dados os pontos: $reto A abre parênteses reto x com reto A subscrito vírgula espaço reto y com reto A subscrito fecha parênteses vírgula espaço espaço reto B abre parênteses reto x com reto B subscrito vírgula espaço reto y com reto B subscrito fecha parênteses espaço espaço espaço reto e espaço espaço reto C parêntese esquerdo reto x com reto C subscrito vírgula espaço reto y com reto C subscrito parêntese direito$ .

Estes três pontos estarão alinhados se o determinante da seguinte matriz for igual a zero.

$começar estilo tamanho matemático 22px det espaço abre colchetes tabela linha com célula com reto x com reto A subscrito fim da célula célula com reto y com reto A subscrito fim da célula 1 linha com célula com reto x com reto B subscrito fim da célula célula com reto y com reto B subscrito fim da célula 1 linha com célula com reto x com reto C subscrito fim da célula célula com reto y com reto C subscrito fim da célula 1 fim da tabela fecha colchetes espaço igual a espaço 0 fim do estilo$

Exemplo

Coeficiente angular de uma reta

O coeficiente angular $reto m$ de uma reta é a tangente de sua inclinação $alfa$ em relação ao eixo x.

$começar estilo tamanho matemático 22px reto m espaço igual a espaço tg espaço reto alfa fim do estilo$

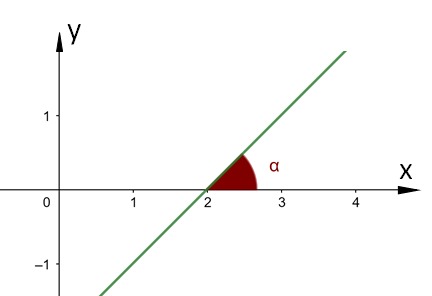
Para obter o coeficiente angular a partir de dois pontos:

$começar estilo tamanho matemático 22px reto m igual a numerador reto y com reto B subscrito menos reto y com reto A subscrito sobre denominador reto x com reto B subscrito menos reto x com reto A subscrito fim da fração fim do estilo$

Se m > 0 a reta é ascendente, caso contrário, se m < 0, a reta é decrescente.

Equação geral da reta

$começar estilo tamanho matemático 22px ax espaço mais espaço by espaço mais espaço reto c espaço igual a espaço 0 fim do estilo$

Onde a, b e c são números reais constantes e, a e b não são simultaneamente nulos.

Exemplo

Equação da reta conhecendo um ponto e o coeficiente angular

Dado um ponto $reto A abre parênteses reto x com 0 subscrito vírgula espaço reto y com 0 subscrito fecha parênteses$ e o coeficiente angular $reto m$ .

A equação da reta será:

$começar estilo tamanho matemático 22px reto y menos reto y com 0 subscrito igual a reto m parêntese esquerdo reto x menos reto x com 0 subscrito parêntese direito fim do estilo$

Exemplo

Forma reduzida da equação da reta

$começar estilo tamanho matemático 22px reto y igual a mx mais reto n fim do estilo$

Onde:
m é o coeficiente angular;
n é o coeficiente linear.

n é ordenada em que a reta intersecta o eixo y.

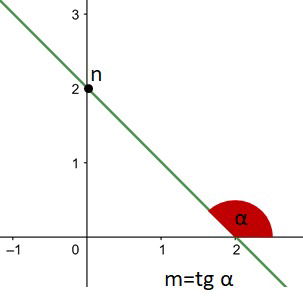
Exemplo

Veja Equação da Reta.

Posição relativa entre duas retas paralelas em um plano

Duas retas distintas são paralelas quando seus coeficientes angulares são iguais.

Se uma reta r possui coeficiente angular $reto m com reto r subscrito$ , e uma reta s possui coeficiente angular $reto m com reto s subscrito$ , estas são paralelas quando:

$começar estilo tamanho matemático 22px reto m com reto r subscrito igual a reto m com reto s subscrito fim do estilo$

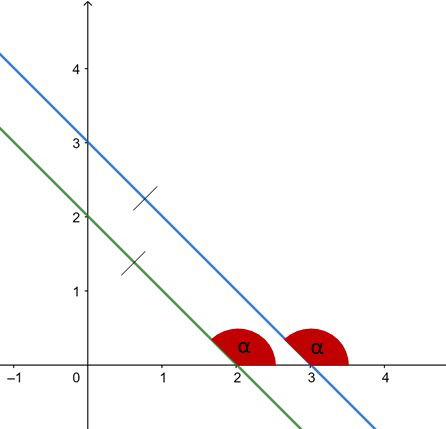
Para isto, suas inclinações devem ser iguais.

$m com s subscrito igual a t g espaço alfa com s espaço subscrito fim do subscrito m com r subscrito igual a t g espaço alfa com r espaço subscrito fim do subscrito$

As tangentes são iguais quando os ângulos são iguais.

Posição relativa entre duas retas concorrentes em um plano

Duas retas são concorrentes quando seus coeficientes angulares são diferentes.

$Error converting from MathML to accessible text.$

Por sua vez, os coeficientes angulares diferem quando seus ângulos de inclinação em relação ao eixo x, são diferentes.

$alfa com r subscrito não igual alfa com s subscrito$

Retas perpendiculares

Duas restas são perpendiculares quando o produto entre seus coeficientes angulares é igual a -1.

Duas retas r e s, distintas, com coeficientes angulares $m com r subscrito$ e $m com s subscrito$ , são perpendiculares se, e somente se:

$começar estilo tamanho matemático 22px reto m com reto r subscrito. reto m com s subscrito igual a menos 1 fim do estilo$

$começar estilo tamanho matemático 22px reto m com reto r subscrito igual a menos 1 sobre reto m com reto s subscrito fim do estilo$

Outro modo de saber se duas retas são perpendiculares é a partir de suas equações na forma geral.

Sendo as equações das retas r e s:

$r dois pontos espaço a com r subscrito x mais b com r subscrito y mais espaço c com r subscrito espaço s dois pontos espaço a com s subscrito x mais b com s subscrito y mais c com s subscrito$

Duas retas suas perpendiculares quando:

$começar estilo tamanho matemático 22px reto a com reto r subscrito. reto a com reto s subscrito mais reto b com reto r subscrito. reto b com reto s subscrito igual a 0 fim do estilo$

Veja Retas Perpendiculares.

Circunferência

Circunferência é o lugar geométrico no plano em que todos os pontos P(x, y) estão a mesma distância r do seu centro C(a, b), onde r é a medida de ser raio.

Equação da circunferência na forma reduzida

$começar estilo tamanho matemático 22px abre parênteses reto x menos reto a fecha parênteses ao quadrado mais abre parênteses reto y menos reto b fecha parênteses ao quadrado igual a reto r ao quadrado fim do estilo$

Onde:
r é o raio, a distância entre qualquer ponto de seu arco e o centro C.
a e b são as coordenadas do centro C.

Equação geral da circunferência

$começar estilo tamanho matemático 22px reto x ao quadrado mais reto y ao quadrado menos 2 ax menos 2 by mais abre parênteses reto a ao quadrado mais reto b ao quadrado menos reto r ao quadrado fecha parênteses igual a 0 fim do estilo$

É obtida ao desenvolver os termos elevados ao quadrado da equação reduzida da circunferência.

É muito comum aparecer a forma geral da equação da circunferência nos exercícios, também conhecida como forma normal.

Cônicas

A palavra cônica vêm de cone e se refere as curvas obtidas ao seccioná-lo. Elipse, hipérbole e parábola são curvas chamadas de cônicas.

Elipse

Elipse é uma curva fechada obtida pela secção de um cone circular reto por um plano oblíquo ao eixo, que não passa pelo vértice e não é paralelo as suas geratrizes.

Em um plano, o conjunto de todos os pontos cuja soma das distâncias a dois pontos fixos internos é constante.

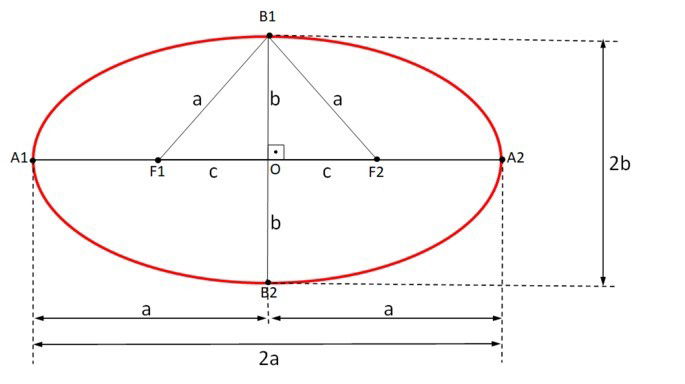
Elementos da elipse:

F1 e F2 são os focos da elipse;
2c é distância focal da elipse. É a distância entre F1 e F2;
O ponto O é centro da elipse. É o ponto médio entre F1 e F2;
A1 e A2 são os vértices da elipse;
O segmento $pilha reto A com 1 subscrito reto A com 2 subscrito com barra acima$ eixo maior e igual a 2a.
O segmento $pilha reto B com 1 subscrito reto B com 2 subscrito com barra acima$ eixo menor e igual a 2b.
Excentricidade $e espaço igual a espaço c sobre a$ onde 0 < e < 1.

Equação reduzida da elipse

Considere um ponto P(x, y) contido na elipse onde x é a abcissa e y a ordenada deste ponto.

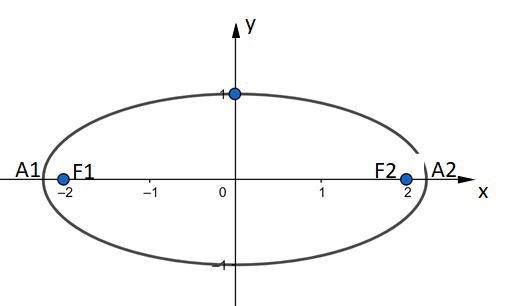
Centro da elipse na origem do sistema de coordenadas e eixo maior (AA) no eixo x.

$começar estilo tamanho matemático 22px reto x ao quadrado sobre reto a ao quadrado mais reto y ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

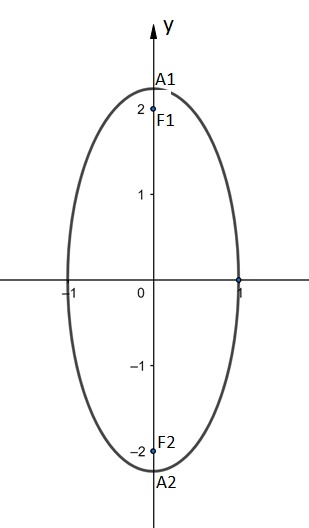
Centro da elipse na origem do sistema de coordenadas e eixo maior (AA) no eixo y.

$começar estilo tamanho matemático 22px reto x ao quadrado sobre reto b ao quadrado mais reto y ao quadrado sobre reto a ao quadrado igual a 1 fim do estilo$

Equação reduzida da elipse com eixos paralelos aos eixos coordenados

Considerando um ponto $reto O parêntese esquerdo reto x com 0 subscrito vírgula espaço reto y com 0 subscrito parêntese direito$ como a origem do sistema cartesiano e, um ponto $reto C parêntese esquerdo reto x com 0 subscrito vírgula espaço reto y com 0 subscrito parêntese direito$ como centro da elipse.

Eixo maior AA, paralelo ao eixo x.

$começar estilo tamanho matemático 22px parêntese esquerdo reto x menos reto x com 0 subscrito parêntese direito ao quadrado sobre reto a ao quadrado mais parêntese esquerdo reto y menos reto y com 0 subscrito parêntese direito ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

Eixo maior AA, paralelo ao eixo y.

$Error converting from MathML to accessible text.$

Hipérbole

Hipérbole é um conjunto de pontos em um plano onde a diferença entre dois pontos fixos F1 e F2 resulta em um valor constante e positivo.

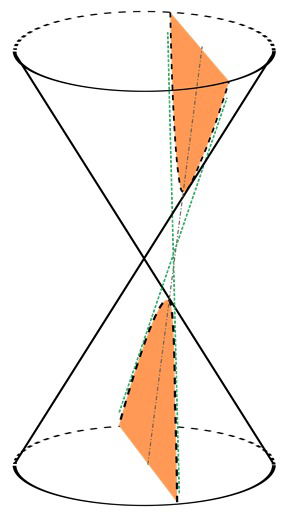
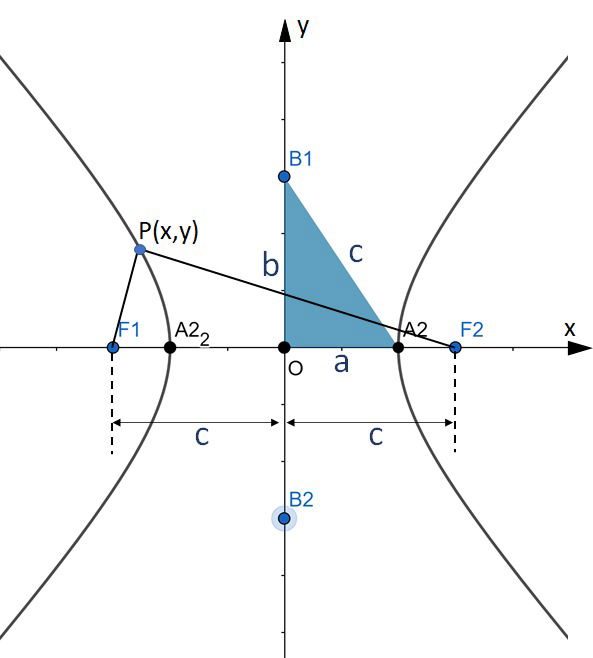
Elementos da hipérbole:

F1 e F2 são os focos da hipérbole.
2c = $pilha reto F 1 reto F 2 com barra acima$ é a distância focal.
Centro da hipérbole é o ponto O, médio do segmento F1F2.
A1 e A2 são os vértices.
2a = A1A2 é o eixo real ou transverso.
2b = B1B2 é o eixo imaginário ou conjugado.
$reto e igual a reto c sobre reto a espaço$ é a excentricidade.

Pelo triângulo B1OA2

$reto c ao quadrado igual a reto a ao quadrado mais reto b ao quadrado$

Equação reduzida da hipérbole

Com eixo real sobre o eixo x e centro na origem.

$começar estilo tamanho matemático 22px reto x ao quadrado sobre reto a ao quadrado menos reto y ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

Com eixo real sobre o eixo y e centro na origem.

$começar estilo tamanho matemático 22px reto y ao quadrado sobre reto a ao quadrado menos reto x ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

Equação da hipérbole com eixos paralelos aos eixos coordenados

Eixo real AA paralelo ao eixo x e centro $reto C parêntese esquerdo reto x com 0 subscrito vírgula reto y com 0 subscrito parêntese direito$ .

$começar estilo tamanho matemático 22px parêntese esquerdo reto x menos reto x com 0 subscrito parêntese direito ao quadrado sobre reto a ao quadrado menos parêntese esquerdo reto y menos reto y com 0 subscrito parêntese direito ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

Eixo real AA paralelo ao eixo y e centro $reto C parêntese esquerdo reto x com 0 subscrito vírgula reto y com 0 subscrito parêntese direito$ .

$começar estilo tamanho matemático 22px parêntese esquerdo reto y menos reto y com 0 subscrito parêntese direito ao quadrado sobre reto a ao quadrado menos parêntese esquerdo reto x menos reto x com 0 subscrito parêntese direito ao quadrado sobre reto b ao quadrado igual a 1 fim do estilo$

Parábola

Parábola é o lugar geométrico em que o conjunto de pontos P(x, y) estão a mesma distância de um ponto fixo F e de uma reta d.

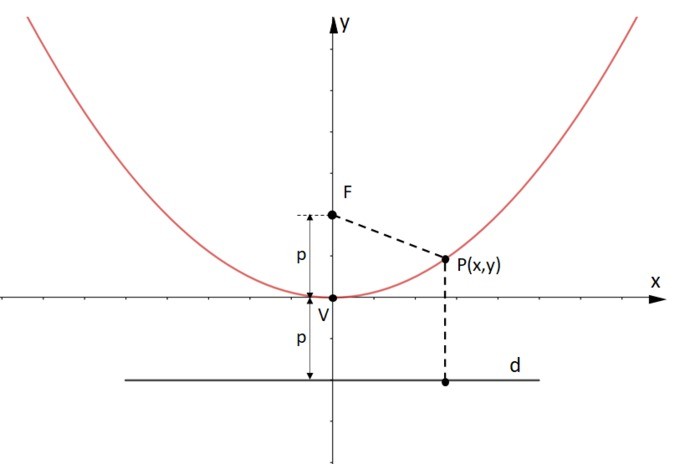
Elementos da parábola:

F é o foco da parábola;
d é a reta diretriz;
Eixo de simetria é a reta que passa pelo foco F e é perpendicular à diretriz.
V é vértice da parábola.
p é o segmento de mesmo comprimento entre o foco F e o vértice V e, entre o vértice e a diretriz d.

Equações reduzidas da parábola

Com vértice na origem e eixo de simetria sobre o eixo y.

$começar estilo tamanho matemático 22px reto x ao quadrado igual a 4 py fim do estilo$

Se p>0 concavidade para cima.
Se p<0 concavidade para baixo.

Com vértice na origem e eixo de simetria sobre o eixo x.

$começar estilo tamanho matemático 22px reto y ao quadrado igual a 4px fim do estilo$

Se p>0 concavidade para direita.
Se p<0 concavidade para esquerda.

Com eixo de simetria paralelo ao eixo y e vértice $reto V abre parênteses reto x com 0 subscrito vírgula reto y com 0 subscrito fecha parênteses$ .

$começar estilo tamanho matemático 22px abre parênteses reto x menos reto x com 0 subscrito fecha parênteses ao quadrado igual a 4 reto p abre parênteses reto y menos reto y com 0 subscrito fecha parênteses fim do estilo$

Com eixo de simetria paralelo ao eixo x e vértice $reto V abre parênteses reto x com 0 subscrito vírgula reto y com 0 subscrito fecha parênteses$ .

$começar estilo tamanho matemático 22px parêntese esquerdo reto y menos reto y com 0 subscrito parêntese direito ao quadrado igual a 4 reto p parêntese esquerdo reto x menos reto x com 0 subscrito parêntese direito fim do estilo$

Pratique com Exercícios sobre Geometria Analítica.

Aprenda mais em:
Plano Cartesiano
Distância entre dois pontos
Cônicas
Cálculo do Coeficiente Angular

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações