Isomeria Geométrica

Isomeria Geométrica é o tipo de isomeria espacial, também conhecida como estereoisomeria, que se caracteriza por apresentar uma dupla de isômeros com dimensões tridimensionais diferentes. Isso acontece em decorrência da presença de ligantes diferentes.

Também conhecida como isomeria cis-trans, ela somente é possível em cadeias abertas que apresentem dupla ligação de carbono, ou seja, em cadeias abertas insaturadas.

A isomeria geométrica, entretanto, não acontece apenas em cadeias abertas, também pode acontecer em compostos cíclicos.

Cis e Trans

Quando os ligantes dos carbonos da substância química encontram-se estruturalmente posicionados do mesmo lado, a isomeria é chamada de cis.

Quando os ligantes dos carbonos da substância química encontram-se estruturalmente posicionados do lado oposto, a isomeria é chamada de trans.

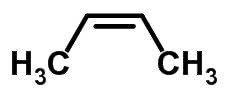
Forma molecular de cis-but-2-eno C₄H₈

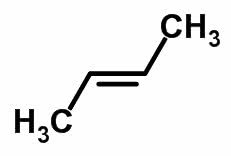
Forma molecular de trans-but-2-eno C₄H₈

Isomeria Geométrica em Compostos Cíclicos

Em compostos cíclicos, os ligantes têm de ser diferentes no mínimo em dois carbonos.

Nesse caso, podem ocorrer isômeros cis e trans ao mesmo tempo.

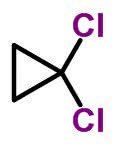
Forma molecular de cis-diclorociclopropano C₃H₄Cl₂

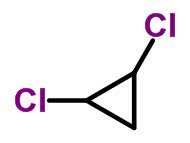
Forma molecular de trans-diclorociclopropano C₃H₄Cl₂

Nomenclatura

É por isso que a nomenclatura dos isômeros geométricos contém os prefixo cis e trans no nome, o que serve de identificação das substâncias.

Cis e trans podem ser substituídos pelas iniciais Z e E, respectivamente. É essa a nomenclatura aconselhada pela IUPAC (União Internacional de Química Pura e Aplicada).

Isso porque Z, do alemão zusammen, significa “juntos”. E, do alemão entegegen, significa “opostos”.

Leia também:

• O que é isomeria?
• Tipos de someria
• Isomeria Óptica
• Isomeria Plana

Exercícios

1. (Fuvest) Quantos isômeros estruturais e geométricos, considerando também os cíclicos, são previstos com a fórmula molecular C₃H₅Cl?

a) 2.
b) 3.
c) 4.
d) 5.
e) 7.

2. (Vunesp-SP) Apresenta isomeria geométrica:

a) pent-2-eno
b) but-1,2-dieno
c) propeno
d) tetrabromo etileno
e) 1,2-dimetil benzeno

3. (Vunesp-SP) Entre os compostos

I. C₂H₆O.
II. C₃H₆O.
III. C₂H₂Cℓ₂.

apresentam isomeria geométrica:

a) I, apenas.
b) II, apenas.
c) III, apenas.
d) I e II, apenas.
e) II e III, apenas.