Leis de Kepler: entenda quais são (com exemplos e exercícios resolvidos)
As Leis de Kepler são três leis propostas no século XVII pelo astrônomo e matemático alemão Johannes Kepler (1571–1630), apresentadas em sua obra Astronomia Nova (1609).
Elas descrevem os movimentos dos planetas, seguindo modelos heliocêntricos, ou seja, com o Sol no centro do sistema solar.
As afirmações a respeito dos movimentos dos planetas por Kepler, não propõem o porquê destes movimentos, não estão empenhadas em descrever as causas desses movimentos. Estas proposições tratam de descrever apenas os movimentos e suas órbitas.
Kepler elaborou suas afirmações de forma descritiva, baseado em observações astronômicas feitas por Tycho Brahe. Seus estudos pertencem ao campo da Física conhecida por cinemática.
Vale lembrar que as Leis de Kepler descrevem não apenas o movimento dos planetas ao redor do Sol, mas de qualquer corpo celeste que orbita outro que possua mais massa. Por exemplo, o movimento da Lua ao redor da Terra ou mesmo de satélites artificiais.
Primeira Lei de Kepler (Lei das Órbitas Elípticas)
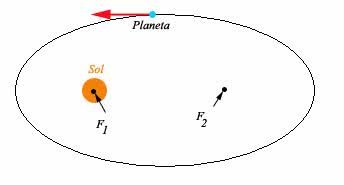
A 1ª Lei descreve a forma das órbitas dos planetas. Kepler propôs que os planetas giram em torno do Sol em órbitas elípticas, com o Sol em um dos focos.
Elipse é uma forma geométrica plana que você pode entender como sendo uma circunferência achatada. Em seu interior há dois pontos de grande importância no estudo de sua forma: os focos.
É exatamente sobre um de seus focos que se posiciona o corpo de maior massa (como o Sol, por exemplo).
Nesta Lei, Kepler corrige o modelo proposto por Copérnico que descrevia como circular o movimento orbital dos planetas.
Segunda Lei de Kepler (Lei das Áreas Iguais)
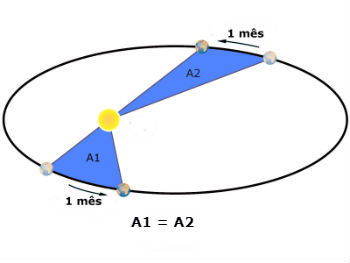
A 2ª lei de Kepler assegura que o segmento (raio vetor) que une o Sol a um planeta varre áreas iguais em intervalos de tempo iguais.
Raio vetor é uma linha imaginária no espaço que liga o Sol ao planeta que está sendo estudado. Conforme o movimento do planeta ocorre, essa linha vai 'varrendo o espaço'.
Em dois momentos diferentes ao longo da trajetória do planeta, se consideramos um mesmo intervalo de tempo e comparamos as áreas varridas no espaço, encontramos o mesmo valor.
A título de exemplo, suponha o raio vetor entre a Terra e o Sol ao longo do mês de janeiro. Durante seu movimento ele terá varrido, marcado, uma grande área com o formato próximo a um pedaço de pizza. Em outro momento do ano, no mês de julho, por exemplo, outra grande área será marcada e, sua medida será igual a de janeiro.
Uma consequência deste fato é que a velocidade do planeta ao longo da sua trajetória orbital muda, ela não é constante.
A velocidade do planeta será maior quando estiver mais próximo do seu periélio (menor distância entre o planeta e o Sol) e menor, quando o planeta se encontra próximo do seu afélio (maior distância do planeta ao Sol).
Terceira Lei de Kepler (Lei dos Períodos)
Período é o tempo para um planeta dar uma volta ao redor do Sol, ou seja, completar sua órbita. Por isso, também é conhecido como período orbital. Usaremos a letra T para representá-lo.
Outra medida fundamental para compreender a Lei dos Períodos é a distância média do planeta ao Sol, também chamada de semieixo maior da órbita ou, simplesmente, raio médio.
A média vem do fato de que essa distância muda ao longo do ano. Ora o planeta está mais perto, ora mais distante. Usaremos a letra r para representar essa medida.
A 3ª lei de Kepler indica que o quadrado do período orbital (T) de cada planeta, é proporcional ao cubo do raio médio (r).
Por isso, quanto mais distante o planeta estiver do sol, mais tempo levará para completar a translação.
Matematicamente, a terceira Lei de Kepler é descrita da seguinte maneira:
Onde:
T: período (tempo de translação).
r: o raio médio da órbita do planeta.
K: valor constante
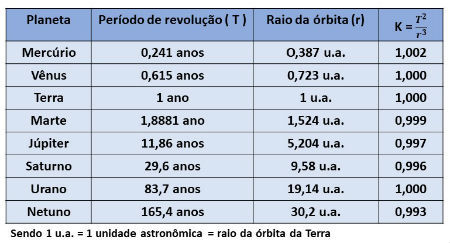
A seguinte tabela mostra os valores de T, r e K para os planetas do Sistema Solar.
Exercícios sobre as Leis de Kepler
Exercício 1
(Enem - 2009) O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bordo e uma câmera nova, que iria substituir uma outra danificada por um curto-circuito no telescópio Hubble. Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do Hubble. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio. Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno."
Considerando o texto e as leis de Kepler, pode-se afirmar que a frase dita pelo astronauta
a) se justifica porque o tamanho do telescópio determina a sua massa, enquanto seu pequeno peso decorre da falta de ação da aceleração da gravidade.
b) se justifica ao verificar que a inércia do telescópio é grande comparada à dele próprio, e que o peso do telescópio é pequeno porque a atração gravitacional criada por sua massa era pequena.
c) não se justifica, porque a avaliação da massa e do peso de objetos em órbita tem por base as leis de Kepler, que não se aplicam a satélites artificiais.
d) não se justifica, porque a força-peso é a força exercida pela gravidade terrestre, neste caso, sobre o telescópio e é a responsável por manter o próprio telescópio em órbita.
e) não se justifica, pois a ação da força-peso implica a ação de uma força de reação contrária, que não existe naquele ambiente. A massa do telescópio poderia ser avaliada simplesmente pelo seu volume.
Exercício 2
(UFRGS - 2011) Considere o raio médio da órbita de Júpiter em tomo do Sol igual a 5 vezes o raio médio da órbita da Terra.
Segundo a 3ª Lei de Kepler, o período de revolução de Júpiter em tomo do Sol é de aproximadamente
a) 5 anos
b) 11 anos
c) 25 anos
d) 110 anos
e) 125 anos
Exercício 3
(Enem - 2009) Na linha de uma tradição antiga, o astrônomo grego Ptolomeu (100-170 d.C.) afirmou a tese do geocentrismo, segundo a qual a Terra seria o centro do universo, sendo que o Sol, a Lua e os planetas girariam em seu redor em órbitas circulares. A teoria de Ptolomeu resolvia de modo razoável os problemas astronômicos da sua época. Vários séculos mais tarde, o clérigo e astrônomo polonês Nicolau Copérnico (1473-1543), ao encontrar inexatidões na teoria de Ptolomeu, formulou a teoria do heliocentrismo, segundo a qual o Sol deveria ser considerado o centro do universo, com a Terra, a Lua e os planetas girando circularmente em torno dele. Por fim, o astrônomo e matemático alemão Johannes Kepler (1571- 1630), depois de estudar o planeta Marte por cerca de trinta anos, verificou que a sua órbita é elíptica. Esse resultado generalizou-se para os demais planetas.
A respeito dos estudiosos citados no texto, é correto afirmar que
a) Ptolomeu apresentou as ideias mais valiosas, por serem mais antigas e tradicionais.
b) Copérnico desenvolveu a teoria do heliocentrismo inspirado no contexto político do Rei Sol.
c) Copérnico viveu em uma época em que a pesquisa científica era livre e amplamente incentivada pelas autoridades.
d) Kepler estudou o planeta Marte para atender às necessidades de expansão econômica e científica da Alemanha.
e) Kepler apresentou uma teoria científica que, graças aos métodos aplicados, pôde ser testada e generalizada.
Para saber mais, leia também Johannes Kepler.
Pratique mais exercícios sobre as Leis de Kepler.
Leis de Kepler e a Gravitação Universal
As Leis de Kepler descrevem o movimento dos planetas, sem se preocupar com as suas causas.
Isaac Newton ao estudar essas Leis, identificou que a velocidade dos planetas ao longo da trajetória é variável em valor e direção.
Para explicar essa variação, ele identificou existirem forças atuando nos planetas e no Sol.
Deduziu que essas forças de atração dependem da massa dos corpos envolvidos e das suas distâncias.
Chamada de Lei de Gravitação Universal, sua expressão matemática é:
Sendo,
F: força gravitacional
G: constante de gravitação universal
M: massa do Sol
m: massa do planeta
r: distância entre os corpos
Pratique com Exercícios sobre a gravitação universal.
ASTH, Rafael. Leis de Kepler: entenda quais são (com exemplos e exercícios resolvidos). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/leis-de-kepler/. Acesso em: