Leis de Kirchhoff: quais são, como usar e exercícios
As Leis de Kirchhoff são utilizadas para encontrar as intensidades das correntes em circuitos elétricos que não podem ser reduzidos a circuitos simples.
Constituídas por um conjunto de regras, elas foram concebidas em 1845 pelo físico alemão Gustav Robert Kirchhoff (1824-1887), quando ele era estudante na Universidade de Königsberg.
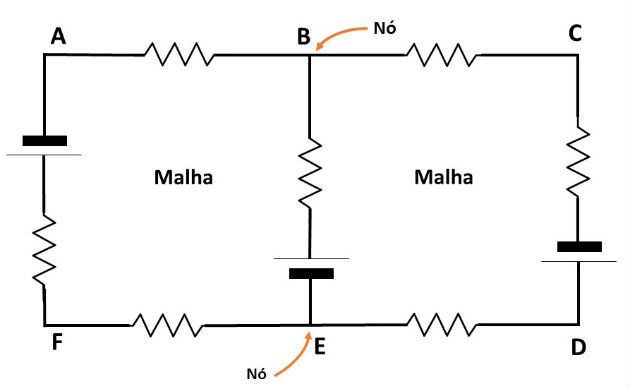
A 1ª Lei de Kirchhoff é chamada de Lei dos Nós, que se aplica aos pontos do circuito onde a corrente elétrica se divide. Ou seja, nos pontos de conexão entre três ou mais condutores (nós).
Já a 2ª Lei é chamada de Lei das Malhas, sendo aplicada aos caminhos fechados de um circuito, os quais são chamados de malhas.
Lei dos Nós (primeira lei de Kirchhoff)
A Lei dos Nós, também chamada de primeira lei de Kirchhoff, indica que a soma das correntes que chegam em um nó é igual a soma das correntes que saem.
Esta lei é consequência da conservação da carga elétrica, cuja soma algébrica das cargas existentes em um sistema fechado permanece constante.
Exemplo
Na figura abaixo, representamos um trecho de um circuito percorrido pelas correntes i1, i2, i3 e i4.
Indicamos ainda o ponto onde os condutores se encontram (nó):
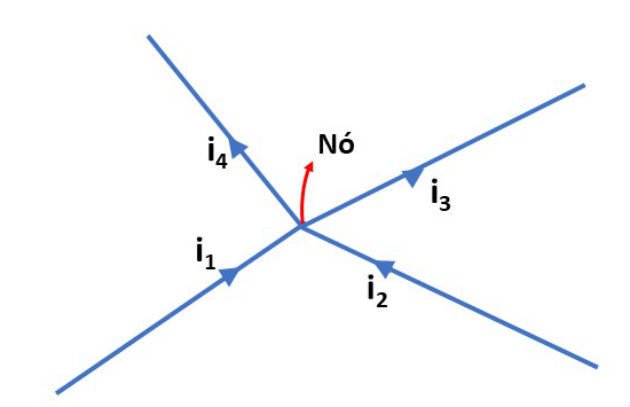
Neste exemplo, considerando que as correntes i1 e i2 estão chegando ao nó, e as correntes i3 e i4 estão saindo, temos:
i1 + i2 = i3 + i4
Em um circuito, o número de vezes que devemos aplicar a Lei dos Nós é igual ao número de nós do circuito menos 1. Por exemplo, se no circuito existir 4 nós, vamos usar a lei 3 vezes (4 - 1).
Veja sobre:
Lei das Malhas (segunda de Kirchhoff)
A Lei das Malhas é uma consequência da conservação da energia. Ela indica que quando percorremos uma malha em um dado sentido, a soma algébrica das diferenças de potencial (ddp ou tensão) é igual a zero.
Para aplicar a Lei das Malhas, devemos convencionar o sentido que percorremos o circuito.
A tensão poderá ser positiva ou negativa, conforme o sentido que arbitramos para a corrente e para percorrer o circuito.
Para isso, consideremos que o valor da ddp (tensão U) em um resistor é dado por:
U = R . i
Onde, R é a resistência e i é a corrente.
Se o sentido da corrente for o mesmo do sentido do percurso será positivo, e negativo se for no sentido contrário.
Para o gerador (fem) e receptor (fcem) utiliza-se o sinal de entrada no sentido que adotamos para a malha.
Como exemplo, considere a malha indicada na figura abaixo:
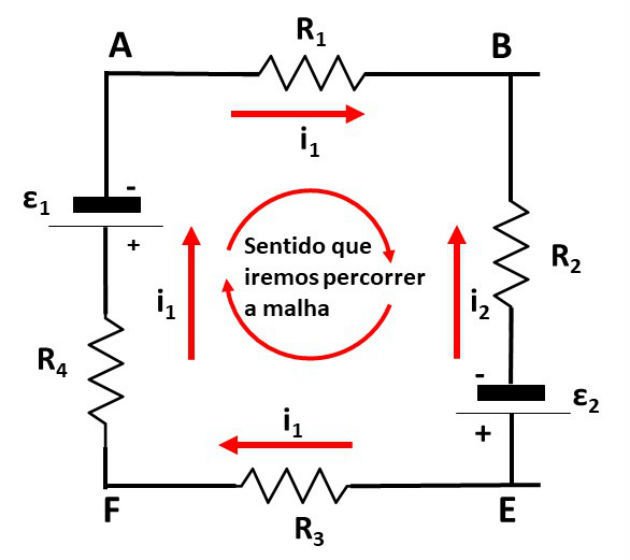
Aplicando a lei das malhas para esse trecho do circuito, teremos:
UAB + UBE + UEF + UFA = 0
Para substituir os valores de cada trecho, devemos analisar os sinais das tensões:
- ε1: positivo, pois ao percorrer o circuito no sentido horário (sentido que escolhemos) chegamos pelo polo positivo;
- R1.i1: positivo, pois estamos percorrendo o circuito no mesmo sentido que definimos o sentido de i1;
- R2.i2: negativo, pois estamos percorrendo o circuito no sentido contrário que definimos para o sentido de i2;
- ε2: negativo, pois ao percorrer o circuito no sentido horário (sentido que escolhemos), chegamos pelo polo negativo;
- R3.i1: positivo, pois estamos percorrendo o circuito no mesmo sentido que definimos o sentido de i1;
- R4.i1: positivo, pois estamos percorrendo o circuito no mesmo sentido que definimos o sentido de i1;
Considerando o sinal da tensão em cada componente, podemos escrever a equação desta malha como:
ε1 + R1.i1 - R2.i2 - ε2 + R3.i1 + R4.i1 = 0
Aprenda mais sobre:
Aplicação da Lei de Kirchhoff passo a passo
Para aplicar as Leis de Kirchhoff devemos seguir os seguintes passos:
- 1º Passo: Definir o sentido da corrente em cada ramo e escolher o sentido em que percorreremos as malhas do circuito. Essas definições são arbitrárias, contudo, devemos analisar o circuito para escolher coerentemente esses sentidos.
- 2º Passo: Escrever as equações relativas à Lei dos Nós e Lei das Malhas.
- 3º Passo: Juntar as equações obtidas pela Lei dos Nós e das Malhas em um sistema de equações e calcular os valores desconhecidos. O número de equações do sistema deve ser igual ao número de incógnitas.
Ao resolver o sistema, encontraremos todas as correntes que percorrem os diferentes ramos do circuito.
Se algum dos valores encontrados for negativo, significa que o sentido da corrente escolhido para o ramo tem, na verdade, sentido contrário.
Exemplo
No circuito abaixo, determine as intensidades das correntes em todos os ramos.
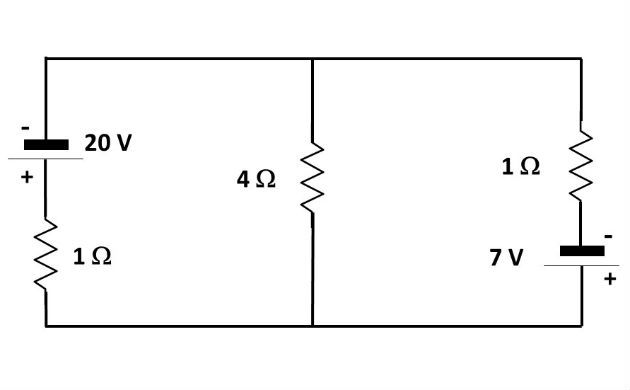
Solução
Primeiro, definimos um sentido arbitrário para as correntes e também o sentido que seguimos na malha.
Neste exemplo, escolhemos o sentido conforme esquema abaixo:
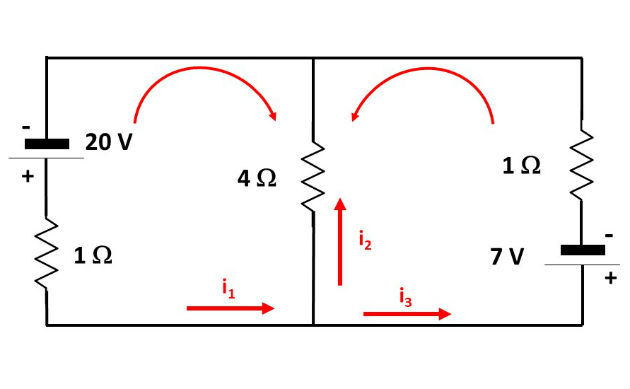
O próximo passo é escrever um sistema com as equações estabelecidas usando a Lei dos Nós e das Malhas. Sendo assim, temos:
Por fim, resolvemos o sistema. Começando substituindo i3 por i1 - i2 nas demais equações:
Resolvendo o sistema por soma, temos:
Agora encontramos o valor de i1, substituindo na segunda equação o valor encontrado para i2:
Finalmente, substituímos esses valores encontrados na primeira equação, para encontrar o valor de i3:
Assim, os valores das correntes que percorrem o circuito são: 3A, 8A e 5A.
Para saber mais, veja também:
Exercícios sobre as Leis de Kirchhof resolvidos
Exercício 1
(ITA - 2013) Considere o circuito elétrico mostrado na figura formado por quatro resistores de mesma resistência, R = 10 Ω, e dois geradores ideais cujas respectivas forças eletromotrizes são ε1 = 30 V e ε2 = 10 V. Pode-se afirmar que as correntes i1, i2, i3 e i4 nos trechos indicados na figura, em ampères, são respectivamente de

a) 2, 2/3, 5/3 e 4
b) 7/3, 2/3, 5/3 e 4
c) 4, 4/3, 2/3 e 2
d) 2, 4/3, 7/3 e 5/3
e) 2, 2/3, 4/3 e 4
Exercício 2
(Unesp - 1993) Três resistores, P, Q e S, cujas resistências valem 10, 20 e 20 ohms, respectivamente, estão ligados ao ponto A de um circuito. As correntes que passam por P e Q são 1,00 A e 0,50 A, como mostra a figura adiante.
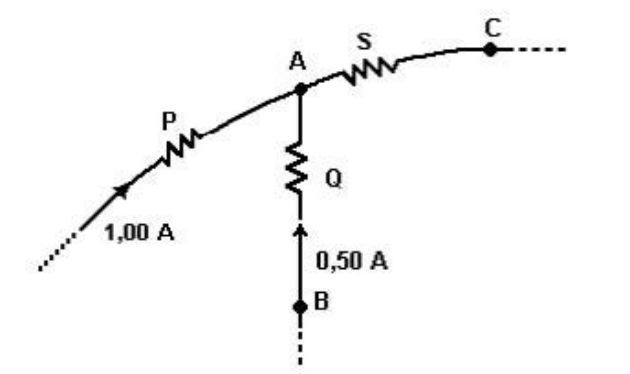
Determine as diferenças de potencial:
a) entre A e C;
b) entre B e C.
Pratique com Exercícios sobre capacitores.
ASTH, Rafael. Leis de Kirchhoff: quais são, como usar e exercícios. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/leis-de-kirchhoff/. Acesso em:


