Matriz Transposta

Rosimar Gouveia

Professora de Matemática e Física

A transposta de uma matriz A é uma matriz que apresenta os mesmos elementos de A, só que colocados em uma posição diferente. Ela é obtida transportando-se ordenadamente os elementos das linhas de A para as colunas da transposta.

Portanto, dada uma matriz A = (a_ij)_{m x n} a transposta de A é A^t = (a’_ji) _{n x m}.

Sendo,

i: posição na linha
j: posição na coluna
a_ij: um elemento da matriz na posição ij
m: número de linhas da matriz
n: número de colunas da matriz
A^t: matriz transposta de A

Note que a matriz A é de ordem m x n, enquanto sua transposta A^t é de ordem n x m.

Exemplo

Encontre a matriz transposta da matriz B.

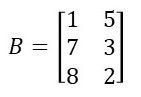
Como a matriz dada é do tipo 3x2 (3 linhas e 2 colunas) a sua transposta será do tipo 2x3 (2 linhas e 3 colunas).
Para construir a matriz transposta, devemos escrever todas as colunas de B como linhas de B^t. Conforme indicado no esquema abaixo:

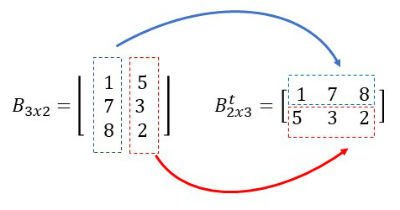
Assim, a matriz transposta de B será:

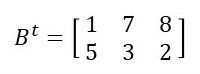
Veja também: Matrizes

Propriedades da Matriz Transposta

• (A^t)^t = A: essa propriedade indica que a transposta de uma matriz transposta é a matriz original.
• (A + B)^t = A^t + B^t: a transposta da soma duas matrizes é igual a soma da transposta de cada uma delas.
• (A . B)^t = B^t . A^t: a transposta da multiplicação de duas matrizes é igual ao produto das transpostas de cada uma delas, em ordem inversa.
• det(M) = det(M^t): o determinante da matriz transposta é igual ao determinante da matriz original.

Matriz Simétrica

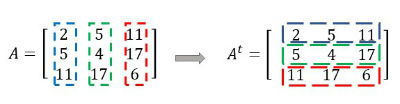
Uma matriz é chamada simétrica quando, para qualquer elemento da matriz A, a igualdade a_ij = a_ji é verdadeira.

As matrizes desse tipo são matrizes quadradas, ou seja, o número de linhas é igual ao número de colunas.

Toda matriz simétrica, satisfaz a seguinte relação:

A = A^t

Matriz Oposta

Importante não confundir a matriz oposta com a transposta. A matriz oposta é aquela que contém os mesmos elementos nas linhas e nas colunas, no entanto, com sinais diferentes. Assim, a oposta de B é –B.

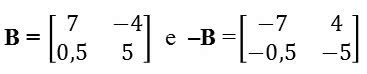
Matriz Inversa

A matriz inversa (indicada pelo número –1) é aquela em que produto de duas matrizes é igual a uma matriz identidade (I) quadrada de mesma ordem.

Exemplo:

A . B = B . A = I_n (quando a matriz B é inversa da matriz A)

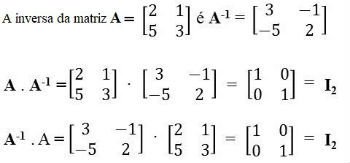
Exercícios de Vestibular com Gabarito

1. (Fei-SP) Dada a Matriz A = , sendo A^t sua transposta, o determinante da matriz A . A^t é:

a) 1
b) 7
c) 14
d) 49

2. (FGV-SP) A e B são matrizes e A^t é a matriz transposta de A. Se 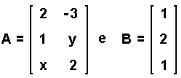, então a matriz A^t . B será nula para:

a) x + y = –3
b) x . y = 2
c) x/y = –4
d) x . y² = –1
e) x/y = –8

3. (UFSM-RS) Sabendo-se que a matriz

é igual a transposta, o valor de 2x + y é:

a) –23
b) –11
c) –1
d) 11
e) 23

Leia Também:

• Matrizes - Exercícios
• Tipos de Matrizes
• Matriz Identidade
• Matrizes e Determinantes
• Multiplicação de Matrizes

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.