Matrizes e Determinantes

Rosimar Gouveia

Professora de Matemática e Física

As Matrizes e os Determinantes são conceitos utilizados na matemática e em outras áreas como, por exemplo, da informática.

São representadas na forma de tabelas que correspondem a união de números reais ou complexos, organizados em linhas e colunas.

Matriz

A Matriz é um conjunto de elementos dispostos em linhas e colunas. As linhas são representadas pela letra 'm' enquanto as colunas pela letra 'n', onde n ≥ 1 e m ≥ 1.

Nas matrizes podemos calcular as quatro operações: soma, subtração, divisão e multiplicação:

Exemplos:

Uma matriz de ordem m por n (m x n)

A = | 1 0 2 4 5|

Logo, A é uma matriz de ordem 1 (com 1 linha) por 5 (5 colunas)

Lê-se Matriz de 1 x 5

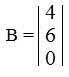
Logo B é uma matriz de ordem 3 (com 3 linha) por 1 (1 colunas)

Lê-se Matriz de 3 x 1

Saiba mais com a leitura dos artigos:

• Matrizes - Exercícios
• Tipos de Matrizes
• Matriz Inversa
• Matriz Identidade
• Matriz Transposta
• Multiplicação de Matrizes
• Teorema de Laplace
• Equação da Reta

Determinante

O Determinante é um número associado a uma matriz quadrada, ou seja, uma matriz que apresenta o mesmo número de linhas e de colunas (m = n).

Neste caso, é chamada de Matriz Quadrada de ordem n. Em outras palavras, toda matriz quadrada possui um determinante, seja ele um número ou uma função associado à ela:

Exemplo:

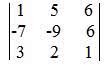
Assim, para calcular o Determinante da Matriz Quadrada:

• Deve se repetir as 2 primeiras colunas

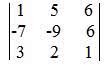
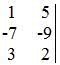
• Encontrar as diagonais e multiplicar os elementos, não esquecendo de trocar o sinal no resultado da diagonal secundária:

1. Diagonal principal (da esquerda para a direita): (1,-9,1) (5,6,3) (6,-7,2)
2. Diagonal secundária (da direita para a esquerda): (5,-7,1) (1,6,2) (6,-9,3)

Portanto, o Determinante da matriz 3x3 = 182.

Aprenda também sobre a Regra de Cramer.

Curiosidades

• Pierre Frédéric Sarrus (1798-1861) foi um matemático francês que inventou um método para o encontrar os determinantes das matrizes quadradas de ordem 3 (3x3) conhecido como a "Regra de Sarrus".
• O "Teorema de Laplace", um método para calcular o determinante de qualquer tipo de matriz quadrada, foi inventado pelo matemático e físico francês Pierre Simon Marquis de Laplace (1749-1827).
• Os determinantes considerados nulos são aqueles em que a soma dos elementos de qualquer das diagonais seja igual a zero.
• São tipos de Matrizes Quadradas: Matriz Identidade, Matriz Inversa, Matriz Singular, Matriz Simétrica, Matriz Positiva Definida e Matriz Negativa. Há também as matrizes transpostas e opostas.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.