MDC - Máximo Divisor Comum

Rafael C. Asth

Professor de Matemática e Física

O máximo divisor comum (MDC ou M.D.C) corresponde ao produto dos divisores comuns entre dois ou mais números inteiros.

Lembre-se que os números divisores são aqueles que ocorrem quando o resto da divisão é igual a zero. Por exemplo, o número 12 é divisível por 1, 2, 3, 4, 6 e 12. Se dividirmos 12 por esses números obteremos um resultado exato, sem que haja um resto na divisão.

Quando um número tem apenas dois divisores, ou seja, ele é divisível somente por 1 e por ele mesmo, eles são chamados de números primos.

Vale notar que todo número natural possui divisores. O menor divisor de um número será sempre o número 1. Por sua vez, o maior divisor de um número é o próprio número.

Obs: Além do MDC temos o MMC (mínimo múltiplo comum) que corresponde ao menor número inteiro positivo de dois ou mais números inteiros.

Atenção!

O zero (0) não é divisor de nenhum número.

Como calcular o MDC?

Para calcular o máximo divisor comum (MDC) entre números, devemos realizar a fatoração por meio da decomposição em fatores primos dos números indicados.

Para exemplificar, vamos calcular através da fatoração o MDC do 20 e 24:

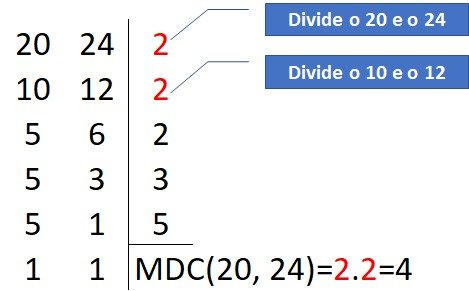
Para saber o MDC dos números, devemos olhar à direita da fatoração e ver quais números dividiram, simultaneamente, nas duas colunas e multiplicá-los.

Assim, pela fatoração podemos concluir que o 4 (2x2) é o maior número que divide ambos e, portanto, é o máximo divisor comum de 20 e 24.

Saiba mais sobre a divisão.

Exemplos

1. Qual o MDC de 18 e 60?

Pela fatoração de ambos os números, temos:

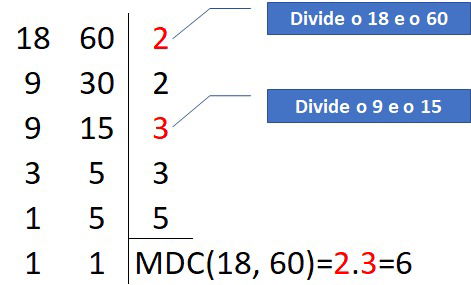
Ao multiplicar os números que dividem ambos, temos que o MDC de 18 e 60 é 6 (2 x 3).

2. Qual o MDC de 6; 12 e 15?

Pela fatoração dos números, temos:

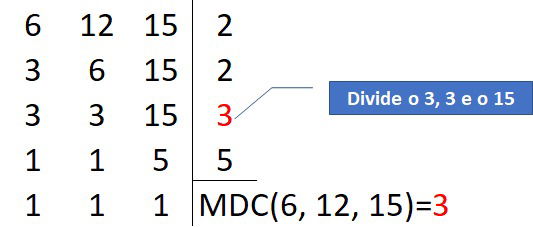
Logo, temos que o MDC de 6; 12 e 15 é o 3.

Propriedades do MDC

• Quando temos dois números consecutivos entre si, podemos concluir que o MDC deles é 1, uma vez que eles serão sempre números primos entre si. Por exemplo: 25 e 26 (o maior número que divide ambos é o 1);
• Quando temos dois ou mais números e um deles é divisor dos outros, podemos concluir que ele é o MDC dos números, por exemplo, 3 e 6. (se 3 é divisor de 6, ele é o MDC de ambos)

Saiba mais sobre os números primos.

Veja também os textos:

• Divisores
• MMC e MDC
• MMC - mínimo múltiplo comum

Exercícios de Vestibular com Gabarito

Questão 1

(Vunesp) Em um colégio de São Paulo, há 120 alunos na 1.ª série do Ensino Médio, 144 na 2.ª e 60 na 3.ª. Na semana cultural, todos esses alunos serão organizados em equipes, com o mesmo número de elementos, sem que se misturem alunos de séries diferentes. O número máximo de alunos que pode haver em cada equipe é igual a:

a) 7
b) 10
c) 12
d) 28
e) 30

Questão 2

(Enem-2015) Um arquiteto está reformando uma casa. De modo a contribuir com o meio ambiente, decide reaproveitar tábuas de madeira retiradas da casa. Ele dispõe de 40 tábuas de 540 cm, 30 de 810 cm e 10 de 1 080 cm, todas de mesma largura e espessura. Ele pediu a um carpinteiro que cortasse as tábuas em peças de mesmo comprimento, sem deixar sobras, e de modo que as novas peças ficassem com o maior tamanho possível, mas de comprimento menor que 2 m.
Atendendo o pedido do arquiteto, o carpinteiro deverá produzir
a) 105 peças
b) 120 peças
c) 210 peças
d) 243 peças
e) 420 peças

Questão 3

(Enem-2015) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos:

1) cada escola deverá receber ingressos para uma única sessão;
2) todas as escolas contempladas deverão receber o mesmo número de ingressos;
3) não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).

O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é:

a) 2
b) 4
c) 9
d) 40
e) 80

Para mais questões, veja:

Exercícios de MMC e MDC.

Exercícios sobre Máximo Divisor Comum (MDC).

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.