Média Aritmética Ponderada

Rafael C. Asth

Professor de Matemática e Física

A Média Aritmética Ponderada ou, Média Ponderada, é usada quando alguns elementos são mais importantes que outros. Esses elementos são ponderados pelos seus pesos.

A Média Ponderada (MP) considera os valores que devem influenciar mais no valor final, os que têm maior peso. Para isso cada elementos do conjunto, é multiplicado por um valor atribuído.

Fórmula da Média Ponderada

$começar estilo tamanho matemático 20px MP igual a numerador reto x com 1 subscrito. reto p com 1 subscrito espaço mais espaço reto x com 2 subscrito. reto p com 2 subscrito espaço mais espaço reto x com 3 subscrito. reto p com 3 subscrito espaço mais espaço... espaço mais espaço reto x com reto n subscrito. reto p com reto n subscrito sobre denominador reto p com 1 subscrito mais espaço reto p com 2 subscrito espaço mais espaço reto p com 3 subscrito espaço mais espaço... espaço mais espaço reto p com reto n subscrito fim da fração fim do estilo$

Onde:
$reto x com 1 subscrito vírgula espaço reto x com 2 subscrito vírgula espaço reto x com 3 subscrito vírgula espaço... espaço reto x com reto n subscrito$ são os elementos do conjunto que queremos determinar a média;

$reto p com 1 subscrito vírgula espaço reto p com 2 subscrito vírgula espaço reto p com 3 subscrito vírgula espaço... espaço reto p com reto n subscrito$ são os pesos.

Cada elemento é multiplicado por seu peso e o resultado das multiplicações é somado. Este resultado é dividido pela soma dos pesos.

Os valores dos pesos são atribuídos por quem está calculando a média, conforme a importância ou necessidade das informações.

Exemplo 1
Para construir uma parede foram comprados 150 blocos na loja A, o que era todo estoque da loja, pelo preço de R$ 11,00 a unidade. Como eram necessários 250 blocos para construir a parede, outros 100 blocos foram comprados na loja B, por R$ 13,00 a unidade. Qual a Média Ponderada do preço do bloco?

Como queremos determinar a média do preço, estes são os elementos e, as quantidades de blocos são os pesos.

$M P espaço igual a espaço numerador 11.150 espaço mais espaço 13.100 sobre denominador 150 espaço mais espaço 100 fim da fração M P espaço igual a espaço numerador 1 espaço 650 espaço mais espaço 1 espaço 300 sobre denominador 250 fim da fração M P espaço igual a espaço numerador 2 espaço 950 sobre denominador 250 fim da fração igual a 11 vírgula 8$

Portanto, a média ponderada do preço foi de R$ 11,80.

Exemplo 2
Um grupo de pessoas com idades diferentes foram entrevistadas e, suas idades anotadas na tabela. Determine a Média Aritmética Ponderada das idades.

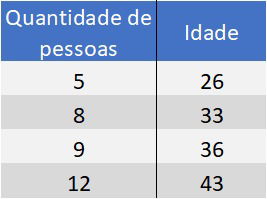
Como queremos a média das idades, estes são os elementos e, a quantidade de pessoas são os pesos.

$M P igual a numerador 26.5 espaço mais espaço 33.8 espaço mais espaço 36.9 espaço mais espaço 43.12 sobre denominador 5 mais 8 mais 9 mais 12 fim da fração M P igual a numerador 130 espaço mais espaço 264 espaço mais espaço 324 espaço mais espaço 516 sobre denominador 34 fim da fração M P espaço igual a espaço numerador 1 espaço 234 sobre denominador 34 fim da fração aproximadamente igual 36 vírgula 3$

A Média Ponderada das idades é de, aproximadamente, 36,3 anos.

Exercícios

Exercício 1

(FAB - 2021) A classificação final de um aluno, num determinado curso é dado pela média ponderada das notas obtidas nas provas de Matemática, Português e Conhecimentos Específicos.

Suponha que as notas de um determinado aluno são as seguintes:

Com base nessas informações, calcule a média ponderada desse aluno e assinale a opção correta.

a) 7.
b) 8.
c) 9.
d) 10.

Ver Resposta

Resposta correta: b) 8.

$M P igual a numerador 10.1 espaço mais espaço 2.7 espaço mais espaço 2.8 sobre denominador 1 espaço mais espaço 2 espaço mais espaço 2 fim da fração M P igual a numerador 10 espaço mais espaço 14 espaço mais espaço 16 sobre denominador 5 fim da fração M P igual a 40 sobre 5 igual a 8$

Exercício 2

(Enem - 2017) A avaliação de rendimento de alunos de um curso universitário baseia-se na média ponderada das notas obtidas nas disciplinas pelos respectivos números de créditos, como mostra o quadro:

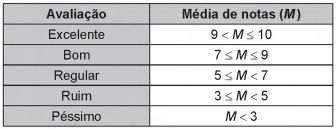
Quanto melhor a avaliação de um aluno em determinado período letivo, maior sua prioridade na escolha de disciplinas para o período seguinte.

Determinado aluno sabe que se obtiver avaliação “Bom” ou “Excelente” conseguirá matrícula nas disciplinas que deseja. Ele já realizou as provas de 4 das 5 disciplinas em que está matriculado, mas ainda não realizou a prova da disciplina I, conforme o quadro.

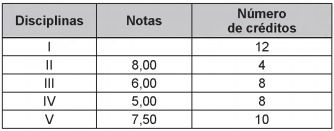
Para que atinja seu objetivo, a nota mínima que ele deve conseguir na disciplina I é

a) 7,00.
b) 7,38.
c) 7,50.
d) 8,25.
e) 9,00.

Ver Resposta

Resposta correta: d) 8,25.

O aluno precisa alcançar pelo menos o conceito bom e, pela primeira tabela, no mínimo, ele deve ficar com média 7.

Vamos utilizar a fórmula da média ponderada onde os números de créditos são os pesos e, a nota que estamos procurando, chamaremos de x.

$M P igual a numerador x.12 espaço mais espaço 8.4 espaço mais espaço 6.8 espaço mais espaço 5.8 espaço mais espaço 7 vírgula 5 espaço. espaço 10 sobre denominador 12 espaço mais espaço 4 espaço mais espaço 8 espaço mais espaço 8 espaço mais espaço 10 fim da fração 7 espaço igual a espaço numerador 12 x espaço mais espaço 32 espaço mais espaço 48 espaço mais espaço 40 espaço mais espaço 75 sobre denominador 42 fim da fração 7 igual a numerador 12 x espaço mais espaço 195 sobre denominador 42 fim da fração 7 espaço. espaço 42 espaço igual a espaço 12 x espaço mais espaço 195 294 espaço igual a espaço 12 x espaço mais espaço 195 294 espaço menos espaço 195 espaço igual a espaço 12 x 99 espaço igual a espaço 12 x 8 vírgula 25 espaço igual a espaço x$

Portanto, a nota mínima que ele deve conseguir na disciplina I é 8,25.

Exercício 3

Um professor de matemática aplica três provas em seu curso (P1 , P2 , P3 ), cada uma valendo de 0 a 10 pontos. A nota final do aluno é a média aritmética ponderada das três provas, sendo que o peso da prova Pn é igual a n2 . Para ser aprovado na matéria, o aluno tem que ter nota final maior ou igual a 5,4. De acordo com esse critério, um aluno será aprovado nessa disciplina, independentemente das notas tiradas nas duas primeiras provas, se tirar na P3 , no mínimo, nota

a) 7,6.
b) 7,9.
c) 8,2.
d) 8,4.
e) 8,6.

Ver Resposta

Resposta correta: d) 8,4.

Os pesos das provas são:

$P 1 igual a 1 ao quadrado igual a 1 P 2 igual a 2 ao quadrado igual a 4 P 3 igual a 3 ao quadrado igual a 9$

Desconsiderando as notas das provas 1 e 2, ou seja, mesmo que tenha tirado zero, a média deve ser 5,4.

Utilizando a fórmula da média ponderada, onde: N1, N2 e N3 são as notas das provas 1, 2 e 3:

$M P igual a numerador N 1. P 1 espaço mais espaço N 2. P 2 espaço mais espaço N 3. P 3 sobre denominador P 1 espaço mais espaço P 2 espaço mais espaço P 3 fim da fração M P igual a numerador 0. P 1 espaço mais espaço 0. P 2 espaço mais espaço N 3.9 sobre denominador 1 mais 4 mais 9 fim da fração 5 vírgula 4 igual a numerador 9. N 3 sobre denominador 14 fim da fração 5 vírgula 4 espaço. espaço 14 espaço igual a espaço 9. N 3 numerador 75 vírgula 6 sobre denominador 9 fim da fração igual a N 3 8 vírgula 4 igual a N 3$

Portanto, a nota mínima deve ser 8,4.

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações