Movimento harmônico simples

Rafael C. Asth

Professor de Matemática e Física

Na Física, o movimento harmônico simples (MHS) é uma trajetória que ocorre na oscilação em torno de uma posição de equilíbrio.

Nesse tipo particular de movimento, existe uma força que direciona o corpo a um ponto de equilíbrio e sua intensidade é proporcional à distância alcançada quando o objeto se afasta do referencial.

Amplitude, período e frequência angular no MHS

Quando um movimento é realizado e alcança uma amplitude, gerando oscilações que se repetem por um período expresso com uma frequência em unidades de tempo, temos um movimento harmônico ou movimento periódico.

A amplitude (A) corresponde a distância entre a posição de equilíbrio e a posição ocupada ao afastar o corpo.

O período (T) é o intervalo de tempo em que o evento de oscilação se complete. Ele é calculado através da fórmula:

$reto T espaço igual a espaço 2 reto pi raiz quadrada de reto m sobre reto k fim da raiz$

Outra maneira de expressar o período, é relacionando-o com a frequência, que representa o número de oscilações realizadas por unidade de tempo.

$reto T espaço igual a espaço 1 sobre f$

A frequência angular ou velocidade angular é dada pela fórmula:

$reto ómega espaço igual a espaço numerador 2 reto pi sobre denominador reto T fim da fração$ ou $reto ómega espaço igual a espaço 2 reto pi f$

Note que ela pode ser calculada relacionando-se com o período (T) ou com a frequência (f).

Força restauradora no MHS

O afastamento de um corpo da sua posição de equilíbrio faz com que uma força aja sobre ele para que retorne a sua posição.

A força que atua no movimento harmônico simples é de restauração, do tipo elástica. Por isso, a força restauradora no MHS é dada por:

$reto F espaço igual a espaço menos espaço Kx$

Onde, K é uma constante e x é o deslocamento.

Por exemplo, se uma mola suspensa verticalmente encontra-se parada e na sua posição de equilíbrio, ela pode sofrer um deslocamento se a esticarmos ou comprimirmos. Portanto, a deformação sofrida é representada na fórmula por x.

Fórmulas do movimento harmônico simples

O movimento harmônico simples pode ser estudado através do movimento circular uniforme. Unindo-se os conceitos, é possível chegar as equações horárias a seguir.

Posição

$reto x espaço igual a espaço reto A espaço cos espaço abre parênteses ωt espaço mais reto ϕ com 0 subscrito fecha parênteses$

A posição (x), em metros, é dada por:

Amplitude do movimento (A), em metros.
Frequência angular ou velocidade angular ( $reto ómega$ ), em radianos por segundo.
Tempo (t), em segundos.
Fase inicial do MHS ( $reto ϕ com 0 subscrito$ ), em radianos.

Velocidade

$reto v espaço igual a espaço – espaço reto ómega espaço reto A espaço sen espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito parêntese direito espaço$

A velocidade de uma partícula (v), em metros por segundo, é dada por:

Velocidade angular ( $reto ómega$ ), em radianos por segundo.
Amplitude (A), em metros.
Tempo (t), em segundos.
Fase inicial ( $reto ϕ com 0 subscrito$ ), em radianos.

Aceleração

$reto alfa espaço igual a espaço – espaço reto ómega ao quadrado espaço reto A espaço cos espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito espaço parêntese direito espaço$ ou $reto alfa espaço igual a espaço – espaço reto ómega ao quadrado espaço reto x$

A aceleração de uma partícula (A), em metros por segundo ao quadrado, depende de:

Velocidade angular ( $reto ómega$ ), em radianos por segundo.
Posição (x), em metros.

Você também pode se interessar por:

Energia no movimento harmônico simples

A energia no movimento harmônico simples está associada com a energia cinética e energia potencial.

A energia cinética é referente à posição da partícula, sendo calculada por:

$reto E com reto c subscrito espaço igual a espaço mv ao quadrado sobre 2$

A energia potencial é referente à velocidade atingida pela partícula durante o movimento. Como é do tipo elástica, a energia é calculada por:

$reto E com reto p subscrito espaço igual a espaço kx ao quadrado sobre 2$

A soma das duas energias resulta na energia mecânica:

$reto E com reto m subscrito espaço igual a espaço reto E com reto c subscrito espaço mais espaço reto E com reto p subscrito$

Vale lembrar que no movimento harmônico simples a energia cinética e potencial variam, pois dependem da posição e da velocidade. Entretanto, a energia mecânica é constante, supondo que não existem forças dissipativas no movimento harmônico simples.

Saiba mais sobre a Energia Mecânica.

Exemplo de MHS: pêndulo simples

O pêndulo simples é um sistema que realiza o movimento harmônico simples. Ele é composto por um fio inextensível e em sua extremidade está fixa uma partícula de dimensões desprezíveis, que se movimenta livremente.

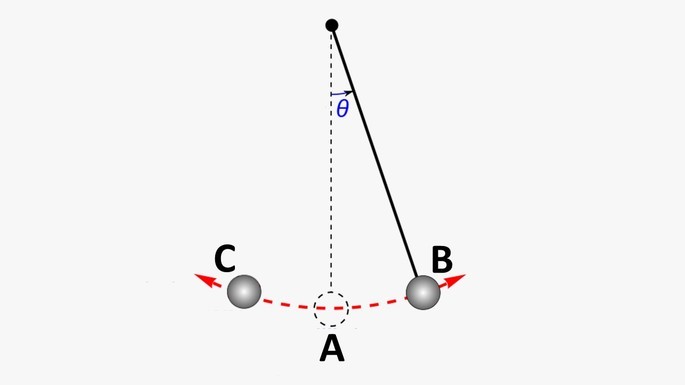
A posição de equilíbrio de um pêndulo, ponto A na imagem acima, acontece quando o instrumento está parado, permanecendo em uma posição fixa.

Deslocar a massa presa na ponta do fio para determinada posição, na imagem representada por B e C, faz com que haja uma oscilação em torno do ponto de equilíbrio.

Fórmulas de período e frequência para o pêndulo

O movimento periódico realizado pelo pêndulo simples pode ser calculado através do período (T).

$reto T espaço igual a espaço 2 reto pi raiz quadrada de reto L sobre reto g fim da raiz$

Onde,

T é o período, em segundos (s).
L é o comprimento do fio, em metros (m).
g é a aceleração da gravidade, em (m/s²).

Já a frequência do movimento pode ser calculada pelo inverso do período, e por isso, a fórmula é:

$f espaço igual a espaço numerador 1 sobre denominador 2 reto pi fim da fração raiz quadrada de reto g sobre reto L fim da raiz$

Saiba mais sobre o pêndulo simples.

Exercícios sobre movimento harmônico simples

Questão 1

Uma esfera de massa igual a 0,2 kg está presa a uma mola, cuja constante elástica k = $0 vírgula 8 espaço reto pi ao quadrado espaço reto N dividido por reto m$ . Afasta-se a mola 3 cm de onde estava em repouso e ao soltá-la o conjunto massa-mola começa a oscilar, executando um MHS. Desprezando as forças dissipativas, determine o período e a amplitude do movimento.

Ver Resposta

Resposta correta: T = 1s e A = 3 cm.

a) O período do movimento.

O período (T) depende apenas da massa, m = 0,2 kg, e da constante, k = $0 vírgula 8 espaço reto pi ao quadrado espaço reto N dividido por reto m$ .

$reto T igual a 2 reto pi espaço. raiz quadrada de numerador 0 vírgula 2 espaço kg sobre denominador 0 vírgula 8 espaço reto pi ao quadrado espaço começar estilo mostrar numerador kg. reto m dividido por reto s ao quadrado sobre denominador reto m fim da fração fim do estilo fim da fração fim da raiz reto T espaço igual a espaço 2 reto pi espaço. raiz quadrada de numerador 1 sobre denominador 4 reto pi ao quadrado espaço fim da fração reto s ao quadrado fim da raiz reto T espaço igual a espaço 2 reto pi espaço. numerador 1 sobre denominador 2 reto pi fim da fração reto s reto T espaço igual a espaço numerador 2 reto pi sobre denominador 2 reto pi fim da fração reto s reto T igual a 1 reto s$

b) A amplitude do movimento.

A amplitude do movimento é 3 cm, distância máxima alcançada pela esfera ao retirá-la da posição de equilíbrio. Portanto, o movimento realizado é de 3 cm para cada lado da posição inicial.

Questão 2

Em uma mola, cuja constante elástica é 65 N/m, está acoplado um bloco de massa 0,68 kg. Movendo o bloco da posição de equilíbrio, x = 0, até uma distância de 0,11 m e soltando-o do repouso em t = 0, determine a frequência angular e a aceleração máxima do bloco.

Ver Resposta

Resposta correta: $reto ómega$ = 9,78 rad/s e $reto alfa com reto m subscrito$ = 11 m/s².

Os dados apresentados no enunciado são:

m = 0,68 kg
k = 65 N/m
x = 0,11 m

A frequência angular é dada pela fórmula: $reto ómega espaço igual a espaço numerador 2 reto pi sobre denominador reto T fim da fração$ e o período é calculado por $reto T espaço igual a espaço 2 reto pi raiz quadrada de reto m sobre reto k fim da raiz$ , então:

$reto ómega espaço igual a espaço numerador 2 reto pi sobre denominador reto T fim da fração espaço igual a espaço numerador 2 reto pi sobre denominador 2 reto pi raiz quadrada de começar estilo mostrar reto m sobre reto k fim do estilo fim da raiz fim da fração igual a numerador 1 sobre denominador raiz quadrada de reto m sobre reto k fim da raiz fim da fração igual a raiz quadrada de reto k sobre reto m fim da raiz$

Substituindo os valores da massa (m) e da constante elástica (k) na fórmula acima, calculamos a frequência angular do movimento.

$reto ómega espaço igual a raiz quadrada de reto k sobre reto m fim da raiz igual a raiz quadrada de numerador 65 espaço começar estilo mostrar tipográfico reto N sobre reto m fim do estilo sobre denominador 0 vírgula 68 espaço kg fim da fração fim da raiz aproximadamente igual 9 vírgula 78 espaço rad dividido por reto s$

A aceleração no MHS é calculada por $reto alfa espaço igual a espaço – espaço reto ómega ao quadrado espaço reto A espaço cos espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito espaço parêntese direito espaço$ enquanto que a posição possui a fórmula $reto x espaço igual a espaço reto A espaço cos espaço abre parênteses ωt espaço mais reto ϕ com 0 subscrito fecha parênteses$ . Sendo assim, podemos modificar a fórmula da aceleração.

$reto alfa espaço igual a espaço – espaço reto ómega ao quadrado espaço reto x$

Observe que a aceleração é uma grandeza proporcional ao negativo do deslocamento. Portanto, quando a posição do móvel está em seu menor valor a aceleração apresenta seu maior valor e vice-versa. Por isso, a aceleração é máxima´é calculada por: $reto alfa com reto m subscrito espaço igual a espaço reto ómega ao quadrado espaço reto x$ .

Substituindo os dados do enunciado na fórmula, temos:

$reto alfa com reto m subscrito espaço igual a espaço reto ómega ao quadrado espaço reto x reto alfa com reto m subscrito espaço igual a parêntese esquerdo 9 vírgula 78 espaço rad dividido por reto s parêntese direito ao quadrado espaço. espaço 0 vírgula 11 espaço reto m reto alfa com reto m subscrito espaço aproximadamente igual 11 espaço reto m dividido por reto s ao quadrado$

Sendo assim, os valores para o problema são: $reto ómega espaço igual a espaço 9 vírgula 78 espaço rad dividido por reto s espaço reto e espaço reto alfa com reto m subscrito espaço igual a espaço 11 espaço reto m dividido por reto s ao quadrado$ .

Questão 3

(Mack-SP) Uma partícula descreve um movimento harmônico simples segundo a equação $reto x espaço igual a 0 vírgula 3. cos abre parênteses reto pi sobre 3 mais 2. reto t fecha parênteses$ , no SI. O módulo da máxima velocidade atingida por esta partícula é:

a) π 3 m/s.
b) 0,2 . π m/s.
c) 0,6 m/s.
d) 0,1 . π m/s.
e) 0,3 m/s.

Ver Resposta

Resposta correta: c) 0,6 m/s.

A equação apresentada no enunciado da questão é a equação horária da posição $reto x espaço igual a espaço reto A espaço cos espaço abre parênteses ωt espaço mais reto ϕ com 0 subscrito fecha parênteses$ . Portanto, os dados apresentados são:

Amplitude (A) = 0,3 m
Frequência angular ( $reto ómega$ ) = 2 rad/s
Fase inicial ( $reto ϕ com 0 subscrito$ ) = $tipográfico reto pi sobre 3$ rad

A velocidade no MHS é calculada por $reto v espaço igual a espaço – espaço reto ómega espaço reto A espaço sen espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito parêntese direito espaço$ . Entretanto, quando $sen espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito parêntese direito espaço igual a espaço menos 1$ a velocidade máxima é atingida e, por isso, a fórmula pode ser reescrita como $reto v espaço igual a espaço – espaço reto ómega espaço reto A espaço. espaço menos 1 espaço igual a espaço reto ómega espaço reto A$ .

Substituindo a frequência angular e amplitude na fórmula, podemos encontrar a velocidade máxima.

$reto v espaço igual a espaço reto ómega espaço reto A reto v espaço igual a espaço 2 espaço reto x espaço 0.3 espaço reto v espaço igual a espaço 0 vírgula 6 espaço reto m dividido por reto s$

Sendo assim, o módulo da máxima velocidade atingida por esta partícula é 0,6 m/s.

Questão 4

Se a posição de uma partícula é determinada pela função horária $reto x espaço igual a espaço 2 espaço cos espaço abre parênteses 4 πt espaço mais reto pi sobre 2 fecha parênteses$ , qual a velocidade escalar da partícula quando t = 1 s?

a) $reto v espaço igual a espaço – espaço 6 espaço reto pi espaço reto m dividido por reto s$
b) $reto v espaço igual a espaço – espaço 8 espaço reto pi espaço reto m dividido por reto s$
c) $reto v espaço igual a espaço – espaço 4 espaço reto pi espaço reto m dividido por reto s$
d) $reto v espaço igual a espaço – espaço 2 espaço reto pi espaço reto m dividido por reto s$
e) n.d.a

Ver Resposta

Resposta correta: b) $reto v espaço igual a espaço – espaço 8 espaço reto pi espaço reto m dividido por reto s$ .

Segundo a função horária temos os seguintes dados:

Amplitude (A) = 2 m
Frequência angular ( $reto ómega$ ) = $4 reto pi$ rad/s
Fase inicial ( $reto ϕ com 0 subscrito$ ) = $tipográfico reto pi sobre 2$ rad

Para calcular a velocidade utilizaremos a fórmula $reto v espaço igual a espaço – espaço reto ómega espaço reto A espaço sen espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito parêntese direito espaço$ .

Primeiramente, vamos resolver o seno da fase do MHS: sen $parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito parêntese direito espaço$ .

Observe que precisamos calcular o seno da soma e, portanto, utilizamos a fórmula:

Por isto, precisamos dos seguintes dados:

$1. espaço sen espaço 4 reto pi espaço igual a espaço sen espaço parêntese esquerdo 2.2 reto pi parêntese direito espaço igual a espaço sen espaço abre parênteses 2.360 º fecha parênteses espaço igual a espaço 0 2. espaço sen espaço tipográfico reto pi sobre 2 espaço igual a espaço sen espaço 90 º espaço igual a espaço 1 3. espaço cos espaço 4 reto pi espaço igual a espaço cos espaço parêntese esquerdo 2.2 reto pi parêntese direito espaço igual a espaço cos espaço abre parênteses 2.360 º fecha parênteses espaço igual a espaço 1 4. espaço cos espaço tipográfico reto pi sobre 2 espaço igual a espaço cos espaço 90 º espaço igual a espaço 0$

Agora, substituímos os valores e calculamos o resultado.

$sen espaço parêntese esquerdo reto A espaço mais espaço reto B parêntese direito espaço igual a espaço sen espaço reto A. cos espaço reto B espaço mais espaço sen espaço reto B. cos espaço reto A sen espaço parêntese esquerdo 4 espaço reto pi espaço mais espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração parêntese direito espaço igual a espaço sen espaço 4 espaço reto pi. cos espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração espaço mais espaço sen tipográfico numerador espaço reto pi espaço sobre denominador 2 fim da fração. cos espaço 4 espaço reto pi sen espaço parêntese esquerdo 4 espaço reto pi espaço mais espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração parêntese direito espaço igual a 0.0 espaço mais espaço 1.1 sen espaço parêntese esquerdo 4 espaço reto pi espaço mais espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração parêntese direito espaço igual a 1$

Colocando o resultado na função horária, calculamos a velocidade da seguinte forma:

$reto v espaço igual a espaço – espaço reto ómega espaço reto A espaço sen espaço parêntese esquerdo reto ómega espaço reto t espaço mais espaço reto ϕ com 0 subscrito espaço parêntese direito espaço reto v espaço igual a espaço – espaço 4 espaço reto pi espaço. espaço 2 espaço sen espaço parêntese esquerdo 4 espaço reto pi.1 espaço mais espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração parêntese direito espaço reto v espaço igual a espaço – espaço 4 espaço reto pi espaço. espaço 2 espaço sen espaço parêntese esquerdo 4 espaço reto pi espaço mais espaço tipográfico numerador reto pi espaço sobre denominador 2 fim da fração parêntese direito espaço reto v espaço igual a espaço – espaço 4 espaço reto pi espaço. espaço 2 espaço. espaço 1 reto v espaço igual a espaço – espaço 8 espaço reto pi espaço reto m dividido por reto s$

Veja também

Para mais exercícios de Física:

Exercícios de Física (resolvidos) para 2º ano do ensino médio

Referências Bibliográficas

RAMALHO, NICOLAU e TOLEDO. Fundamentos da Física - Vol. 2. 7. ed. São Paulo: Editora Moderna, 1999.

MÁXIMO, A., ALVARENGA, B. Curso de Física - Vol. 2. 1. ed. São Paulo: Editora Scipione, 2006.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.