Multiplicação de Matrizes: como multiplicar e exercícios resolvidos

Rafael C. Asth

Professor de Matemática e Física

A multiplicação de matrizes corresponde ao produto entre duas matrizes. O número de linhas da matriz é definida pela letra m e o número de colunas pela letra n.

Já as letras i e j representam os elementos presentes nas linhas e colunas respectivamente.

$reto A igual a parêntese esquerdo reto a com ij subscrito parêntese direito com mxn subscrito$

Exemplo: A_3x3(a matriz A possui três linhas e três colunas)

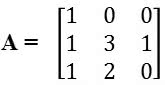
Obs: Importante ressaltar que na multiplicação de matrizes, a ordem dos elementos afeta o resultado. Ou seja, ela não é comutativa:

A . B ≠ B . A

Como multiplicar matrizes?

Para multiplicar duas matrizes devemos seguir uma ordem de operações específicas, onde cada linha da primeira matriz, multiplica todas as colunas da segunda matriz.

Multiplicamos os elementos correspondentes da linha e da coluna e somamos os produtos, assim:

1º elemento da linha x 1º da coluna + 2º elemento da linha x 2º elemento da coluna + … . O processo continua até que todos os elementos tenham sido multiplicados.

Exemplo

Multiplique a matriz A pela B, obtendo uma matriz C.

$abre colchetes tabela linha com 1 2 linha com 3 4 fim da tabela fecha colchetes sinal de multiplicação abre colchetes tabela linha com 2 5 linha com 6 3 fim da tabela fecha colchetes$

A 1ª linha da matriz A multiplica a primeira coluna da matriz B, obtendo o elemento c11.

1 . 2 + 2 . 6 = 14

Para obter o elemento c12, multiplicamos a 1ª linha de A pela 2º coluna de B.

1 . 5 + 2 . 3 = 11

Como já multiplicamos a 1ª linha de A por todas as colunas de B, passamos para 2ª linha de A, que irá multiplicar cada coluna de B.

Para obter o elemento c21, multiplicamos a 2ª linha de A pela 1ª coluna de B.

3 . 2 + 4 . 6 = 30

Para obter o elemento c22, multiplicamos a 2ª linha de A pela segunda coluna de B.

3 . 5 + 4 . 3 = 27

A matriz C fica assim:

$abre colchetes tabela linha com célula com reto c 11 fim da célula célula com reto c 12 fim da célula linha com célula com reto c 21 fim da célula célula com reto c 22 fim da célula fim da tabela fecha colchetes igual a abre colchetes tabela linha com 14 11 linha com 30 27 fim da tabela fecha colchetes$

De forma geral:

Sejam as matrizes $reto A espaço igual a espaço parêntese esquerdo reto a com ij subscrito parêntese direito com mxn subscrito$ e $reto B espaço igual a espaço parêntese esquerdo reto b com jk subscrito parêntese direito com nxp subscrito$

$reto A espaço. espaço reto B espaço igual a espaço matriz espaço reto C espaço igual a espaço parêntese esquerdo reto c com ik subscrito parêntese direito com mxp subscrito$

donde,

$reto c com ik subscrito espaço igual a espaço reto a com reto i 1 subscrito fim do subscrito espaço. espaço reto b com 1 reto k subscrito fim do subscrito espaço mais espaço reto a com reto i 2 subscrito fim do subscrito espaço. espaço reto b com 2 reto k subscrito fim do subscrito espaço mais espaço... espaço mais espaço reto a com in subscrito espaço. espaço reto b com nk subscrito$

_{Quando é possível multiplicar matrizes?}

Para ser possível multiplicar matrizes, é primordial que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz.

O número n de colunas da matriz A é igual ao número n de linhas da matriz B.

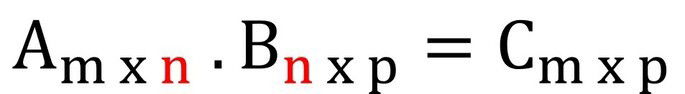
A matriz C, resultado da multiplicação A . B, tem as dimensões m x p, ou seja, o número de linhas da primeira matriz e o número de colunas da segunda.

Exemplo

Verificar se é possível realizar a multiplicação de matrizes abaixo e identificar quais as dimensões da matriz C, resultante da multiplicação.

$reto A com 3 espaço reto x espaço 2 subscrito fim do subscrito espaço. espaço reto B com 2 espaço reto x espaço 4 subscrito fim do subscrito espaço igual a$

É possível multiplicar, pois A possui duas colunas e B possui duas linhas.

A matriz resultante C, possuirá 3 linhas e 4 colunas.

$reto A com 3 espaço reto x espaço 2 subscrito fim do subscrito espaço. espaço reto B com 2 espaço reto x espaço 4 subscrito fim do subscrito igual a reto C com 3 espaço reto x espaço 4 subscrito fim do subscrito$

Veja também: Matrizes

Exemplo de Multiplicação de Matrizes

No exemplo abaixo, temos que a matriz A é do tipo 2x3 e a matriz B é do tipo 3x2. Portanto, o produto entre elas (matriz C) resultará numa matriz 2x2.

$começar estilo tamanho matemático 20px reto A igual a abre colchetes tabela linha com 2 3 1 linha com célula com menos 1 fim da célula 0 2 fim da tabela fecha colchetes espaço espaço reto e espaço espaço reto B igual a abre colchetes tabela linha com 1 célula com menos 2 fim da célula linha com 0 5 linha com 4 1 fim da tabela fecha colchetes reto A com 2 reto x 3 subscrito fim do subscrito espaço. espaço reto B com 3 reto x 2 subscrito fim do subscrito igual a reto C com 2 reto x 2 subscrito fim do subscrito fim do estilo$

Assim, a matriz C genérica é:

$reto C igual a abre colchetes tabela linha com célula com reto c com 11 subscrito fim da célula célula com reto c com 12 subscrito fim da célula linha com célula com reto c com 21 subscrito fim da célula célula com reto c com 22 subscrito fim da célula fim da tabela fecha colchetes$

Inicialmente, multiplicaremos os elementos da linha 1 de A com os da coluna 1 de B. Encontrados os produtos, somamos esses valores:

c11 = 2 . 1 + 3 . 0 + 1 . 4 = 6

Por conseguinte, multiplicaremos e somar os elementos da linha 1 de A com a coluna 2 de B:

c12 = 2 . (-2) + 3 . 5 + 1 . 1 = 12

Depois disso, passaremos para a linha 2 de A e multiplicar e somar com a coluna 1 de B:

c21 = (-1) . 1 + 0 . 0 + 2 . 4 = 7

Ainda na linha 2 de A, multiplicaremos e somar com a coluna 2 de B:

c22 = (-1) . (-2) + 0 . 5 + 2 . 1 = 4

Por fim, temos que a multiplicação de A . B é:

$começar estilo tamanho matemático 20px reto C igual a abre colchetes tabela linha com 6 12 linha com 7 4 fim da tabela fecha colchetes fim do estilo$

Multiplicação de um Número Real por uma Matriz

No caso de multiplicar um número real por uma matriz, deve-se multiplicar cada elemento da matriz por esse número:

Matriz identidade

Matriz identidade é a matriz quadrada de ordem n (2x2, 3x3, 4x4, ... nxn), em que os elementos da diagonal principal são iguais a 1 e, o restante dos elementos são iguais a 0.

Exemplos de matriz identidade de ordens 2 e 3.

$reto I com 2 igual a subscrito fim do subscrito abre colchetes tabela linha com 1 0 linha com 0 1 fim da tabela fecha colchetes espaço espaço espaço espaço espaço espaço reto I com 3 subscrito igual a abre colchetes tabela linha com 1 0 0 linha com 0 1 0 linha com 0 0 1 fim da tabela fecha colchetes$

Matriz Inversa

A matriz inversa é um tipo de matriz que utiliza a propriedade da multiplicação:

A . B = B . A = In (quando a matriz B é inversa da matriz A)

Uma matriz multiplicada por sua inversa é igual a matriz identidade.

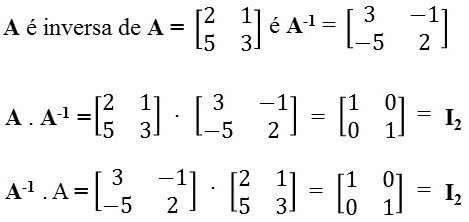
Note que a matriz inversa de A é representada por A^-1.

Aprenda mais sobre matriz inversa.

Exercícios de multiplicação de matrizes

Questão 1

(PUC-RS) Sendo

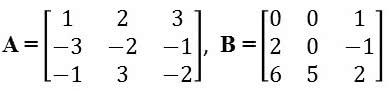
e C = A . B, o elemento C₃₃ da matriz C é:

a) 9
b) 0
c) -4
d) -8
e) -12

Ver Resposta

Resposta correta: d) -8

Como $reto A com 3 reto x 3 subscrito fim do subscrito espaço reto e espaço reto B com 3 reto x 3 subscrito fim do subscrito$ é possível haver multiplicação, pois o número de colunas de A é igual ao número de linhas de B.

A matriz C genérica será:

$C espaço igual a espaço abre colchetes tabela linha com célula com c com 11 subscrito fim da célula célula com c com 12 subscrito fim da célula célula com c com 13 subscrito fim da célula linha com célula com c com 21 subscrito fim da célula célula com c com 22 subscrito fim da célula célula com c com 23 subscrito fim da célula linha com célula com c com 31 subscrito fim da célula célula com c com 32 subscrito fim da célula célula com bold italic c com negrito 33 subscrito fim da célula fim da tabela fecha colchetes$

c33 é o resultado da multiplicação matricial entre a terceira linha de A com a terceira coluna de B.

c33 = -1.1 + 3.(-1) + (-2).2 = -1 -3 -4 = -8

Assim, c33 = -8.

Questão 2

(UF-AM) Sendo

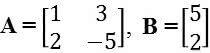
e AX = 2B. Então a matriz X é igual a:

Ver Resposta

Resposta correta: alternativa c)

Passo 1: calcular 2 x B.

Sendo um número real que multiplica uma matriz, basta multiplicá-lo por cada elemento da matriz B.

$2 B espaço igual a espaço abre colchetes tabela linha com célula com 2 espaço. espaço 5 fim da célula linha com célula com 2 espaço. espaço 2 fim da célula fim da tabela fecha colchetes espaço igual a espaço abre colchetes tabela linha com 10 linha com 4 fim da tabela fecha colchetes$

Passo 2: determinar as dimensões da matriz X

Para ser possível a multiplicação entre A e X, o número de colunas de A deve ser igual ao linhas de X.

Como B tem dimensões 2x1, a matriz X tem que ser do tipo $X com 2 espaço x espaço 1 subscrito fim do subscrito$ .

Passo 3: matriz genérica X

$reto X espaço igual a espaço abre colchetes tabela linha com célula com x com 11 subscrito fim da célula linha com célula com x com 21 subscrito fim da célula fim da tabela fecha colchetes$

Passo 4: montando a equação matricial.

$A X espaço igual a 2 B abre colchetes tabela linha com 1 3 linha com 2 célula com menos 5 fim da célula fim da tabela fecha colchetes. abre colchetes tabela linha com célula com x com 11 subscrito fim da célula linha com célula com x com 12 subscrito fim da célula fim da tabela fecha colchetes igual a abre colchetes tabela linha com 10 linha com 4 fim da tabela fecha colchetes$

Passo 5: fazendo o produto matricial.

$abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com 1 espaço. espaço x com 11 subscrito espaço mais espaço 3 espaço. espaço x com 12 subscrito igual a espaço 10 espaço fim da célula linha com célula com espaço 2 espaço. espaço x com 11 subscrito espaço mais espaço parêntese esquerdo menos 5 parêntese direito. x com 12 subscrito espaço igual a espaço 4 fim da célula fim da tabela fecha abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com x com 11 subscrito espaço mais espaço 3 x com 12 subscrito espaço igual a espaço 10 espaço negrito equação negrito espaço negrito I fim da célula linha com célula com espaço 2 x com 11 subscrito espaço menos 5 x com 12 subscrito espaço igual a espaço 4 espaço negrito equação negrito espaço negrito II fim da célula fim da tabela fecha$

Como temos duas equações e duas incógnitas, basta resolver o sistema 2 x 2 para determinar x11 e x12.

Passo 6: resolver o sistema de equações

Isolando x11 na equação I

$x com 11 subscrito espaço igual a espaço 10 espaço menos espaço 3 x com 12 subscrito$

Substituindo na equação II

$2 parêntese esquerdo 10 espaço menos espaço 3 x com 12 subscrito parêntese direito espaço menos espaço 5 x com 12 subscrito espaço igual a espaço 4 20 espaço menos espaço 6 x com 12 subscrito espaço menos espaço 5 x com 12 subscrito espaço igual a espaço 4 espaço 20 espaço menos 11 x com 12 subscrito espaço igual a espaço 4 espaço menos 11 x com 12 subscrito espaço igual a espaço 4 espaço menos espaço 20 espaço menos 11 x com 12 subscrito espaço igual a espaço menos 16 espaço x com 12 subscrito espaço igual a espaço 16 sobre 11$

Substituindo o valor de x12 na equação I

$x com 11 subscrito espaço mais espaço 3. espaço 16 sobre 11 espaço igual a espaço 10 espaço x com 11 subscrito espaço igual a espaço 10 espaço menos espaço 48 sobre 11 x com 11 subscrito espaço igual a espaço numerador 10 espaço. espaço 11 sobre denominador 11 fim da fração menos 48 sobre 11 x com 11 subscrito espaço igual a espaço 62 sobre 11$

Sendo assim

$X espaço igual a espaço abre colchetes tabela linha com célula com 62 sobre 11 fim da célula linha com célula com 16 sobre 11 fim da célula fim da tabela fecha colchetes$

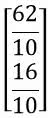
Questão 3

(PUC-MG) Considere as matrizes de elementos reais

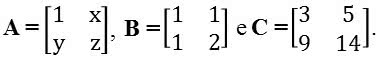
Sabendo-se que A . B = C, pode-se afirmar que a soma dos elementos de A é:

a) 10
b) 11
c) 12
d) 13

Ver Resposta

Resposta correta: c) 12

Passo 1: montar a equação matricial.

AB = C

$abre colchetes tabela linha com 1 x linha com y z fim da tabela fecha colchetes. abre colchetes tabela linha com 1 1 linha com 1 2 fim da tabela fecha colchetes igual a abre colchetes tabela linha com 3 5 linha com 9 14 fim da tabela fecha colchetes$

Passo 2: efetuar as multiplicações.

$abre colchetes tabela linha com célula com 1.1 espaço mais espaço 1. espaço x fim da célula célula com 1.1 espaço mais espaço x.2 fim da célula linha com célula com y.1 espaço mais espaço z.1 fim da célula célula com y.1 espaço mais espaço z.2 fim da célula fim da tabela fecha colchetes igual a abre colchetes tabela linha com 3 5 linha com 9 14 fim da tabela fecha colchetes abre colchetes tabela linha com célula com 1 espaço mais espaço x fim da célula célula com 1 espaço mais espaço 2 x fim da célula linha com célula com y espaço mais espaço z fim da célula célula com y espaço mais espaço 2 z fim da célula fim da tabela fecha colchetes espaço igual a espaço abre colchetes tabela linha com 3 5 linha com 9 14 fim da tabela fecha colchetes$

Passo 3: igualar os termos correspondentes nas duas matrizes.

1 + x = 3 (equação I)

1 + 2x = 5 (equação II)

y + z = 9 (equação III)

y + 2z = 14 (equação IV)

Passo 4: Determinar o valor de x.

Da equação I
1 + x = 3
x = 3 - 1
x = 2

Passo 5: Determinar os valores de y e z.

Das equações III e IV

Temos um sistema de duas equações e duas incógnitas.

Na equação III

y = 9 - z

Substituindo na equação IV

9 - z + 2z = 14
z = 14 - 9
z = 5

Substituindo o valor de z na equação III

y = 9 - 5
y = 4

Passo 6: substituir os valores das incógnitas na matriz A e somar seus elementos.

$A igual a abre colchetes tabela linha com 1 2 linha com 4 5 fim da tabela fecha colchetes$

Sendo assim, a soma dos elementos da matriz é:

1 + 2 + 4 + 5 = 12

Quer saber mais? Leia também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações