Números binários: o que são, conversão e operações

Os números binários são representados por apenas dois algarismos: 0 e 1, pertencendo, por isso, ao sistema de numeração binário, ou de base 2. Cada dígito em um número binário é chamado de 'bit'.

Os números binários são fundamentais na computação e eletrônica digital, pois os computadores utilizam o sistema binário para processar e armazenar dados. Basicamente, o algarismo 0 representa a interrupção de corrente elétrica, enquanto o 1 representa a passagem de eletricidade pelo circuito.

O sistema binário difere do sistema numérico tradicional (indo-arábico), decimal, que utiliza dez algarismos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

Uma mesma quantidade pode ser representada em ambos os sistemas, como duas línguas que utilizam palavras diferentes para representar um mesmo objeto.

É comum representar os números binários com um pequeno 2 entre parênteses, indicando se tratar de um número no sistema binário. O mesmo vale para os números do sistema decimal, representados com um índice 10 entre parênteses.

Exemplo:

O número 11 está em base dez, ou seja, é o número onze. No sistema binário, onze é escrito como 1011.

Imagine que você escreva um bilhete orientando a compra de uma dúzia de ovos. Possivelmente você escreverá o número 12 no bilhete, pois utilizará o sistema decimal de unidades. Se utilizasse o sistema binário para orientar diretamente um computador sobre a compra, escreveria 1100.

Conversão de número decimal para binário

Para converter um número do sistema binário para o decimal utiliza-se um procedimento prático, que faremos em duas partes para facilitar a compreensão.

A primeira parte é uma sucessão de divisões por dois, seguindo os passos:

1. Divide-se o decimal por 2;
2. Divide-se o quociente da primeira divisão novamente por 2;
3. Repete-se o passo 2 até que o quociente seja 1.

A segunda parte é a que “montamos” o número binário, utilizando o último quociente e os restos das divisões.

1. Escreve-se o último quociente;
2. Escreve-se cada resto das divisões anteriores, em ordem inversa da divisão.

Exemplo de conversão de decimal para binário:
Escreva o número 87 na forma de seu equivalente binário.

A primeira parte é a divisão sucessiva por 2, até que o quociente seja menor que 2. Acompanhe:

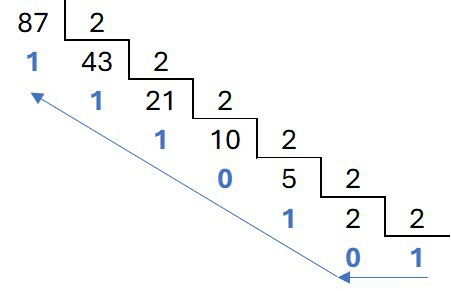
A segunda parte é escrever o número em binário, começando pelo último quociente, o 1, seguindo com os restos, de baixo para cima.

Sendo assim, o número 87 equivale ao binário 1010111.

Conversão de número binário para sistema decimal

A conversão de binário para decimal é realizada pela multiplicação de cada dígito do número binário por uma potência de base dois. Os resultados são somados, obtendo o equivalente de base 10.

Os expoentes dessas potências são números naturais, começando por 0 para o dígito mais à direita e seguindo para esquerda em ordem crescente.

Exemplo de conversão de binário para decimal:
Converta o número binário 1010111 para base decimal.

Utilizemos três passos para o cálculo:

1. Escrevemos os dígitos do binário;
2. Multiplicamos cada dígito por uma potência de 2, sendo 0 o expoente mais à direita;
3. Somamos os resultados das multiplicações entre os dígitos dos binários e as potências.

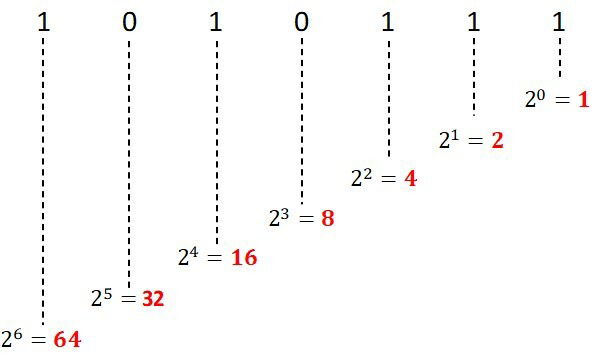
Multipliquemos os algarismos do número binário pelos resultados das potências:

Por fim, basta somar os resultados:

1 + 2 + 4 + 16 + 0 + 64 = 87

Sendo assim, o número binário 1010111 equivale ao número 87 no sistema de base 10.

Operações com números binários

Assim como os números do sistema decimal, também é possível realizar operações com números de base 2.

Adição de números binários

As regras para adição de números binários são as mesmas utilizadas para os de base 10, ou seja:

• 0 + 0 = 1
• 0 + 1 = 1
• 1 + 0 = 1

A exceção é o caso 1 + 1, que no sistema decimal resultaria em 2, no entanto, o algarismo 2 não faz parte do sistema binário.

No sistema de numeração binário 1 + 1 = 10. Nestes casos, escrevemos o 0 e transportamos o 1 para a próxima ordem a ser somada.

Exemplo de adição de números binários
Adicione o número 11 ao 101.

Logo, a adição dos números binário 101 + 11 resulta em 1000.

Subtração de números binários

As seguintes regras para subtração de números binários são as mesmas para os decimais:

• 1 - 1 = 0
• 1 - 0 = 1
• 0 - 0 = 0

A exceção é o caso 0 - 1, resultando em 1.

Nestes casos, vale a regra do empréstimo, que no caso dos números binários funciona subtraindo uma unidade do dígito seguinte.

Exemplo de subtração de números binários
Subtraia 101 do número 1011.

Da direita para esquerda, fizemos:

• 1 - 1 = 0
• 1 - 0 = 1
• 0 - 1 = 1 (regra de subtração de binários)
• 1 - 1 = 0 (regra do “empréstimo”)

Logo, 1011 - 101 = 110.

Você pode se interessar por:

• Sistema de Numeração Decimal
• Exercícios sobre sistema de numeração decimal