Números Reais

Rafael C. Asth

Professor de Matemática e Física

Chamamos de Números Reais o conjunto de elementos representados pela letra maiúscula R, que inclui os:

Números Naturais (N): N = {0, 1, 2, 3, 4, 5,...}
Números Inteiros (Z): Z= {..., -3, -2, -1, 0, 1, 2, 3,...}
Números Racionais (Q): Q = {...,1/2, 3/4, –5/4...}
Números Irracionais (I): I = {...,√2, √3,√7, 3,141592....}

Os números reais podem ser representados de diversas formas, como: inteiros positivos e negativos, frações, decimais, notação científica, raízes, etc.

Quando todos os números reais estão organizados em ordem crescente, temos a Reta Real. Esta reta contém infinitos números, do menos ao mais infinito.

Conjunto dos Números Reais

Para representar a união dos conjuntos, utiliza-se a expressão:

R = N U Z U Q U I ou R = Q U I

Onde:

R: Números Reais
N: Números Naturais
U: União
Z: Números Inteiros
Q: Números Racionais
I: Números Irracionais

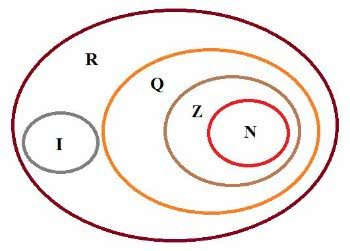
Diagrama dos Conjuntos Numéricos

Diagrama dos conjuntos numéricos

Ao observar a figura acima, podemos concluir que:

O conjunto dos números Reais (R) engloba 4 conjuntos de números: Naturais (N), Inteiros (Z), Racionais (Q) e Irracionais (I)
O conjunto dos números Racionais (Q) é formado pelos conjuntos dos Números Naturais (N) e dos Números Inteiros (Z). Por isso, todo Número Inteiro (Z) é Racional (Q), ou seja, Z está contido em Q.
O Conjunto dos Números Inteiros (Z) inclui os Números Naturais (N); em outras palavras, todo número natural é um número inteiro, ou seja, N está contido em Z.

Propriedades dos números reais

Ordem: Os números reais são ordenados, o que significa que podemos compará-los entre si. Por exemplo, 5 é maior que 3.
Adição: A soma de dois números reais é sempre um número real. Por exemplo, 5 + 3 = 8.
Multiplicação: A multiplicação de dois números reais é sempre um número real. Por exemplo, 5 * 3 = 15.
Divisão: A divisão de dois números reais é um número real. Por exemplo, 5 / 3 = 1 (com resto 2).

Quais números não são reais?

Existem números que não pertencem a nenhum dos subconjuntos dos números reais. Esses números não reais surgiram da necessidade de desenvolver situações matemáticas que não faziam sentido: as raízes de índice par e radicando negativo.

Suponha a raiz:

$raiz quadrada de menos 1 fim da raiz$

Você pode propor como solução o produto (-1) . (-1), no entanto, o resultado desta multiplicação é um número positivo.

$abre parênteses menos 1 fecha parênteses espaço. espaço abre parênteses menos 1 fecha parênteses igual a 1$

O problema de uma raiz de índice par e radicando negativo não possui solução no conjunto dos números reais, ou seja, não há número real que solucione o problema.

Na falta de um número real, só um número imaginado poderia resolver tal problema. Pois foi exatamente o que os matemáticos desenvolveram, um número chamada de imaginário.

Assim, essa raiz assumiu o valor i, de imaginário.

$reto i espaço igual a espaço raiz quadrada de menos 1 fim da raiz$

Essa ideia se desenvolveu a ponto de surgir um novo conjunto numérico, o conjunto dos números complexos $reto números complexos$ .

Saiba mais sobre os números complexos.