Operações com Conjuntos

Rafael C. Asth

Professor de Matemática e Física

As operações com conjuntos são as operações feitas com os elementos que formam uma coleção. São elas: união, intersecção e diferença.

Lembre-se que na matemática os conjuntos representam a reunião de diversos objetos. Quando os elementos que formam o conjunto são números, são chamados de conjuntos numéricos.

Os conjuntos numéricos são:

• Números Naturais (N)
• Números Inteiros (Z)
• Números Racionais (Q)
• Números Irracionais (I)
• Números Reais (R)

União de Conjuntos

A união de conjuntos consiste na combinação dos elementos de conjuntos diferentes. O resultado da união é um novo conjunto que contém todos os elementos dos conjuntos originais. É como juntar todos os elementos de todos os conjuntos envolvidos em um único conjunto.

Se existirem elementos que se repetem nos conjuntos, ele aparecerá uma única vez no conjunto união.

Para representar a união usamos o símbolo U.

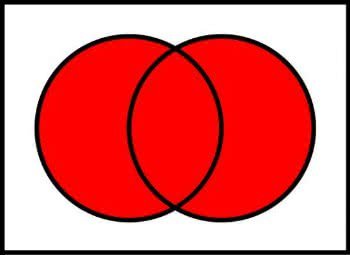
Exemplo:

Dados os conjuntos A = {c, a, r, e, t} e B = {a, e, i, o, u}, represente o conjunto união (A U B).

Para encontrar o conjunto união basta juntar os elementos dos dois conjuntos dados. Temos de ter o cuidado de incluir os elementos que se repetem nos dois conjuntos uma única vez.

Assim, o conjunto união será:

A U B = {c, a, r, e, t, i, o, u}

Intersecção de Conjuntos

A intersecção de conjuntos corresponde aos elementos que se repetem nos conjuntos dados. Ela é representada pelo símbolo ∩.

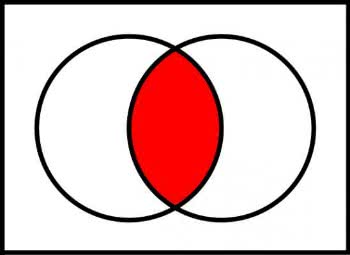
Exemplo:

Dados os conjuntos A = {c, a, r, e, t } e B= B = {a, e, i, o, u}, represente o conjunto intersecção ().

Devemos identificar os elementos comuns nos conjuntos dados que, neste caso, são os elementos a e e, assim o conjunto intersecção ficará:

= {a, e}

Obs: quando dois conjuntos não apresentam elementos em comum, dizemos que a intersecção entre eles é um conjunto vazio.

Nesse caso, esses conjuntos são chamados de disjuntos: A ∩ B = Ø

Diferença de Conjuntos

A diferença de conjuntos é representada pelos elementos de um conjunto que não aparecem no outro conjunto.

Dados dois conjuntos A e B, o conjunto diferença é indicado por A - B (lê-se A menos B).

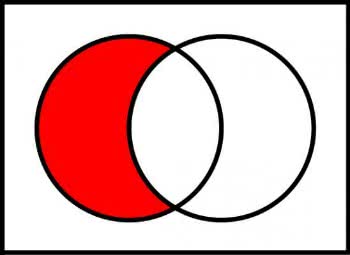
Exemplo:

Dados os conjuntos A = {c, a, r, e, t } e B= B = {a, e, i, o, u}, represente o conjunto intersecção (A - B).

Do conjunto A, retiram-se os elementos comuns em B.

No conjunto A, as letras: a e i, também aparecem em B. Assim:

A - B = {c, r, t}

Também é possível fazer B - A, mas repare que o resultado será diferente.

B - A = {i, o, u}

Conjunto Complementar

Dado um conjunto A, podemos encontrar o conjunto complementar de A determinado pelos elementos de um conjunto universo que não pertençam a A.

Este conjunto pode ser representado por

Quando temos um conjunto B, tal que B está contido em A (), a diferença A - B é igual ao complemento de B.

Exemplo:

Dados os conjuntos A= {a, b, c, d, e, f} e B = {d, e, f, g, h}, indique o conjunto diferença entre eles.

Para encontrar a diferença, primeiro devemos identificar quais elementos pertencem ao conjunto A e que também aparecem ao conjunto B.

No exemplo, identificamos que os elementos d, e e f pertencem a ambos os conjuntos. Assim, retiraremos esses elementos do resultado. Logo, o conjunto diferença de A menos B será dado por:

A – B = {a, b, c}

Propriedades da União e da Intersecção

Dados três conjuntos A, B e C, as seguintes propriedades são válidas:

Propriedade comutativa

Propriedade associativa

Propriedade distributiva

Se A está contido em B ():

Leis de Morgan

Considerando dos conjuntos pertencentes a um universo U, tem-se:

1.º) O complementar da união é igual à intersecção dos complementares:

2.º) O complementar da intersecção é igual à união dos complementares:

Exercícios de operações com conjunto

Exercício 1

(PUC-RJ) Sejam x e y números tais que os conjuntos {0, 7, 1} e {x, y, 1} são iguais. Então podemos afirmar que:

a) a = 0 e y = 5
b) x + y = 7
c) x = 0 e y = 1
d) x + 2y = 7
e) x = y

Exercício 2

(UFU-MG) Sejam A, B e C conjuntos de números inteiros, tais que A tem 8 elementos, B tem 4 elementos, C tem 7 elementos e A U B U C tem 16 elementos. Então, o número máximo de elementos que o conjunto D = (A ∩ B) U (B ∩ C) pode ter, é igual a:

a) 1
b) 2
c) 3
d) 4

Exercício 3

(ITA-SP) Considere as seguintes afirmações sobre o conjunto U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}:

I. Ø ∈ U e n (U) = 10
II. Ø ⊂ U e n (U) = 10
III. 5 ∈ U e {5} C U
IV. {0, 1, 2, 5} ∩ {5} = 5

Pode-se dizer, então, que é (são) verdadeira (s):

a) apenas I e III.
b) apenas II e IV
c) apenas II e III.
d) apenas IV.
e) todas as afirmações.

Leia também:

• Símbolos Matemáticos
• Teoria dos Conjuntos
• Conjuntos Numéricos
• Exercícios sobre Conjuntos
• Exercícios sobre Conjuntos Numéricos

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.