Polias
Polias ou roldanas são dispositivos mecânicos usados para tornar mais cômodo ou reduzir a força necessária para deslocar objetos com um grande peso.
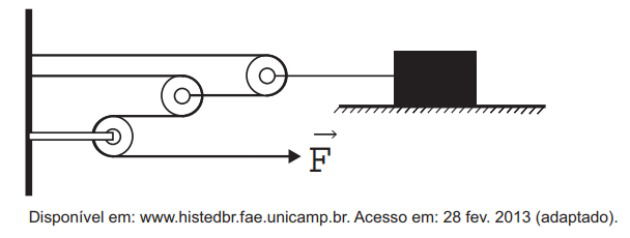
Esse tipo de máquina simples é composta por uma ou mais rodas, que giram em torno de um eixo central e possui um sulco por onde passa uma corda ou fio flexível, conforme a figura abaixo:

Relatos históricos indicam que as roldanas foram usadas pela primeira vez por Arquimedes (287 a.C. - 212 a.C.) para deslocar um navio.
As polias podem ser móveis, quando apresentam movimento de translação, ou fixas, quando não possuem este movimento. Na prática, é muito comum utilizar a associação destes dois tipos de roldanas.
Roldanas Fixas
A roldana fixa tem o seu eixo preso em algum ponto apoio, portanto, apresenta apenas movimento de rotação, não sendo possível o movimento de translação.
Elas modificam apenas o sentido e a direção da força motora que equilibra o peso. Desta forma, são utilizadas para tornar mais cômodo o trabalho de puxar um objeto.
Nas roldanas fixas não verificamos uma redução no esforço necessário para movimentar um objeto. Portanto, o módulo da força motora será igual ao módulo da força resistente (peso da carga a ser transportada).
Exemplo
Determine o valor da força motora necessária para levantar um corpo a uma altura de 10 cm, utilizando uma roldana fixa. Considere que o peso do corpo é igual a 100 N.
Solução
Como na roldana fixa o módulo da força motora é igual a força resistente, que neste caso, é a força peso, então o seu valor será igual a 100 N.
Na imagem abaixo, apresentamos o esquema das forças que atuam neste movimento.
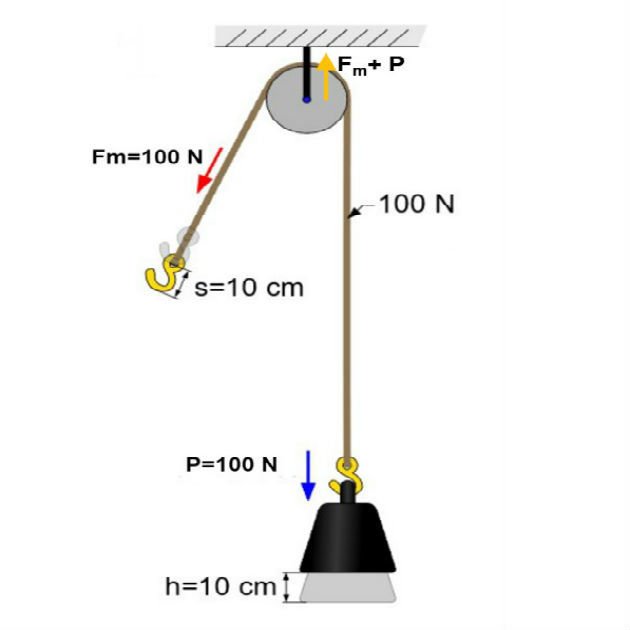
Observe que ao deslocar o corpo 10 cm a corda também se deslocará 10 cm (0,1 m), conforme mostrado na figura.
Note que no ponto onde a roldana está presa age uma força igual a soma das forças resistente (peso) e motora. Desta forma, no exemplo acima o ponto de sustentação da roldana deve ser capaz de suportar uma força de 200 N.
Roldanas Móveis
Diferente das roldanas fixas, as móveis possuem o eixo livre, desta maneira, possuem movimento de rotação e também de translação.
A força resistente que deve ser equilibrada encontra-se no eixo da roldana, enquanto a força motora é aplicada no extremo livre da corda.
A grande vantagem do uso das roldanas móveis é que reduz o valor da força motora necessária para movimentar um determinado corpo, entretanto, um comprimento maior de corda deverá ser puxado.
Exemplo
Determine o valor da força motora necessária para levantar um corpo a uma altura de 10 cm utilizando uma roldana fixa associada a uma roldana móvel. Considere que o peso do corpo é igual a 100 N.
Solução
A polia fixa, conforme vimos, irá apenas modificar o sentido e a direção da força motora, não alterando seu módulo. Contudo, ao incluir uma roldana móvel o valor da força motora será reduzido pela metade, conforme indicado no esquema abaixo:
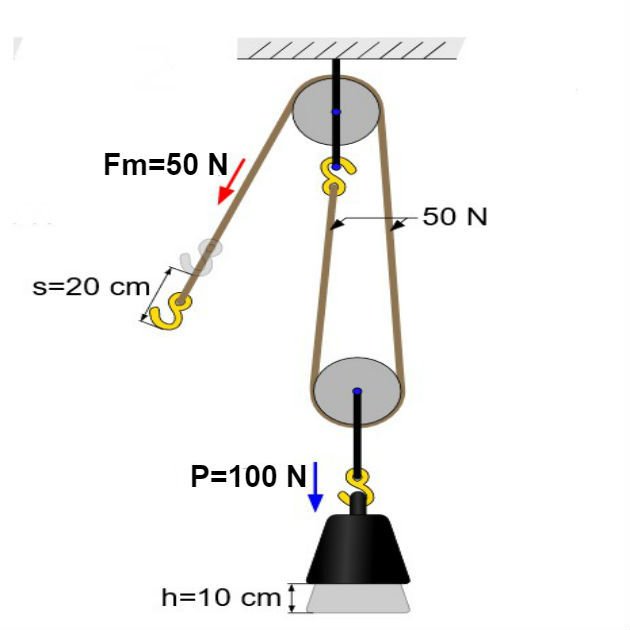
Assim, o módulo da força motora será igual a 50 N. Perceba que, neste caso, a utilização da roldana móvel reduziu pela metade o valor da força necessária para movimentar a mesma carga anterior.
Observe que para o corpo subir 10 cm será necessário puxar um comprimento de corda maior que no exemplo anterior, que neste caso é igual a 20 cm.
Associação de roldanas móveis
Para diminuir ainda mais a força motora necessária para deslocar objetos, utiliza-se a associação de várias polias móveis.
Como vimos, ao usar uma roldana móvel, a força motora será igual a metade da força resistente, sendo que cada polia móvel adicionada irá reduzir pela metade a força que já foi reduzida a metade.
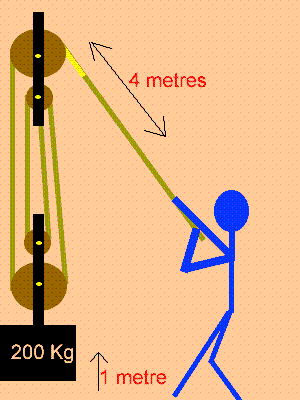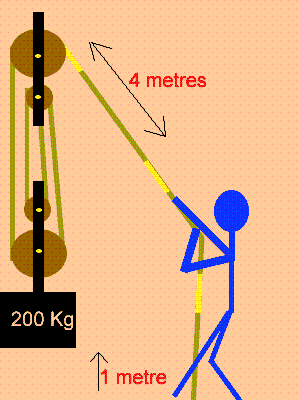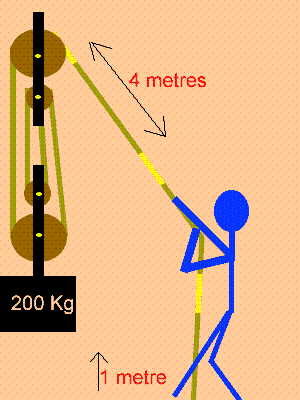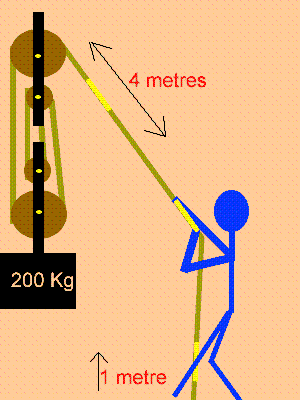
Se associarmos duas polias móveis, temos na primeira polia:
Na segunda polia, a força motora da primeira polia passa a ser a força resistente na segunda. Assim:
Seguindo esse mesmo raciocínio, notamos que o valor da força motora deverá ser encontrado fazendo-se:
Sendo n igual ao número de polias móveis associadas.
Exemplo
Determine o valor da força motora necessária para levantar um corpo a uma altura de 10 cm, utilizando duas roldanas fixas associadas a duas roldanas móveis, sabendo que o peso do corpo é igual a 100 N.
Solução
As duas roldanas fixas não modificam o módulo da força motora. Portanto, para calcular o módulo da força iremos apenas considerar as duas roldanas móveis.
Neste caso, a força motora será encontrada considerando n = 2, aplicando a fórmula, temos:
Portanto, ao usar duas roldanas móveis a força necessária para puxar um corpo com 100 N será 4 vezes menor, ou seja, 25 N.
Abaixo, temos um esquema das forças que atuam no sistema:
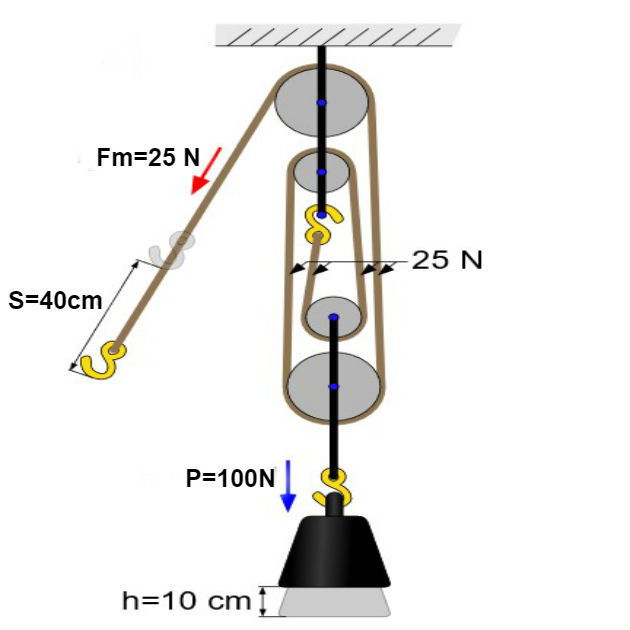
Note que, neste caso, será necessário puxar 40 cm de corda para que o corpo suba 10 cm.
Para saber mais, veja também:
Exercícios Resolvidos
1) Enem - 2016
Uma invenção que significou um grande avanço tecnológico na Antiguidade, a polia composta ou a associação de polias, é atribuída a Arquimedes (287 a.C. a 212 a.C.). O aparato consiste em associar uma série de polias móveis e uma polia fixa. A figura exemplifica um arranjo possível para esse aparato. É relatado que Arquimedes teria demonstrado para o rei Hierão um outro arranjo desse aparato, movendo sozinho, sobre a areia da praia, um navio repleto de passageiros e cargas, algo que seria impossível sem a participação de muitos homens. Suponha que a massa do navio era de 3 000 kg, que o coeficiente de atrito estático entre o navio e a areia era 0,8 e que Arquimedes tenha puxado o navio com uma força , paralela à direção do movimento e de módulo igual a 400 N. Considere os fios e as polias ideais, a aceleração da gravidade igual a 10 m/s2 e que a superfície da praia é perfeitamente horizontal.
O número mínimo de polias móveis usadas, nessa situação, por Arquimedes foi
a) 3.
b) 6.
c) 7.
d) 8.
e) 10.
2) UFMG - 2007
Antônio precisa elevar um bloco até uma altura h. Para isso, ele dispõe de uma roldana e de uma corda e imagina duas maneiras para realizar a tarefa, como mostrado nas figuras:
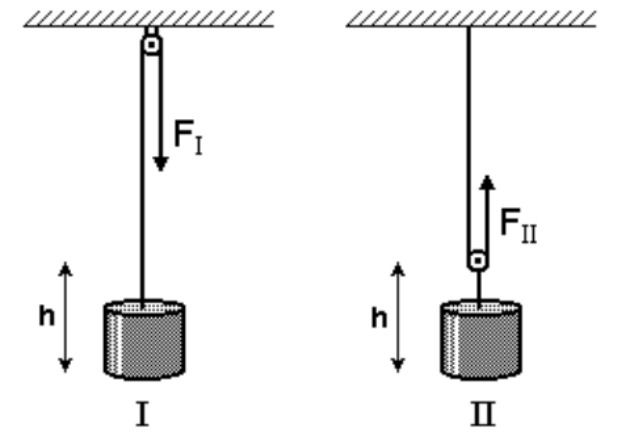
Despreze a massa da corda e a da roldana e considere que o bloco se move com velocidade constante. Sejam FI o módulo da força necessária para elevar o bloco e TI o trabalho realizado por essa força na situação mostrada na Figura I. Na situação mostrada na Figura II, essas grandezas são, respectivamente, FII e TII.
Com base nessas informações, é CORRETO afirmar que
a) 2FI = FII e TI = TII.
b) FI = 2FII e TI = TII.
c) 2FI = FII e 2 TI = TII.
d) FI = 2FII e TI = 2TII.
Para saber mais, veja também:
GOUVEIA, Rosimar. Polias. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/polias/. Acesso em:


