Potência Elétrica

Rosimar Gouveia

Professora de Matemática e Física

Potência elétrica é definida como a rapidez com que um trabalho é realizado. Ou seja, é a medida do trabalho realizado por uma unidade de tempo.

A unidade de potência no sistema internacional de medidas é o watt (W), em homenagem ao matemático e engenheiro James Watts que aprimorou a máquina à vapor.

No caso dos equipamentos elétricos, a potência indica a quantidade de energia elétrica que foi transformada em outro tipo de energia por unidade de tempo.

Por exemplo, uma lâmpada incandescente que em 1 segundo transforma 100 joule de energia elétrica em energia térmica e luminosa terá uma potência elétrica de 100 W.

Fórmula da Potência Elétrica

Para calcular a potência elétrica utilizamos a seguinte fórmula:

P = U . i

Sendo,

P: potência (W)
i: corrente elétrica (A)
U: diferença de potencial (V)

Exemplo

Qual a potência elétrica desenvolvida por um motor, quando a diferença de potencial (ddp) nos seus terminais é de 110 V e a corrente que o atravessa tem intensidade de 20A ?

Solução:

Para calcular a potência, basta multiplicar a corrente pela ddp, sendo assim temos:

P = 20 . 110 = 2200 W

Frequentemente, a potência é expressa em kW, que é um múltiplo do W, de forma que 1 kW = 1000 W. Sendo assim, a potência do motor é de 2,2 kW.

Veja também: Tensão Elétrica

Efeito Joule

Os resistores são dispositivos elétricos que ao serem percorridos por uma corrente, transformam energia elétrica em energia térmica.

Esse fenômeno é chamado de efeito Joule e neste caso dizemos que o resistor dissipa a energia elétrica.

Aquecedores, chuveiros elétricos, secadores de cabelo, lâmpadas incandescentes, ferros de passar roupa são exemplos de equipamentos que utilizam esse efeito.

Cálculo da Potência no Efeito Joule

Para calcular a potência elétrica em um resistor, podemos usar a seguinte expressão:

P = R . i²

Sendo,

P: potência (W)
R: resistência (Ω)
i: corrente (A)

Usando a Lei de Ohm (U = R . i), podemos substituir a corrente na expressão anterior e encontrar a potência em função da diferença de potencial e da resistência. Nesse caso, teremos:

Sendo,

P: potência (W)
U: ddp (V)
R: resistência (Ω)

Exemplo

Um chuveiro elétrico apresenta as seguintes especificações: 2200 W - 220 V, considerando que o chuveiro foi instalado corretamente, determine:

a) o valor da resistência elétrica do chuveiro quando em funcionamento.
b) a intensidade da corrente que o atravessa.

Solução:

a) Para encontrar o valor da resistência podemos usar a fórmula da potência no efeito Joule, assim temos:

b) Para encontrar a corrente, podemos novamente usar a fórmula da potência, só que agora a que aparece a corrente.

Cálculo da Energia Elétrica

Quando um equipamento elétrico fica em funcionamento durante um determinado intervalo de tempo, podemos calcular a energia elétrica que foi consumida.

Para fazer esse cálculo, basta multiplicar a potência do equipamento pelo tempo de funcionamento, assim a energia elétrica é encontrada usando-se a fórmula:

E_el = P. Δt

Sendo,

E_el: energia elétrica (J)
P: potência (W)
Δt: intervalo de tempo (s)

No cotidiano, é muito comum o valor da energia elétrica ser expresso em kWh. Neste caso, para transformar de Joule para kWh, podemos usar a seguinte relação:

1 kWh = 3 600 000 J

Exemplo

Um aquecedor elétrico apresenta uma potência de 3000 W. Qual o custo mensal deste aquecedor ao ficar ligado durante 3 horas todos os dias? Considere que 1 kWh custa R$ 0,40.

Solução:

Primeiro vamos calcular o valor da energia consumida pelo aquecedor em 1 dia:

E_el= 3000.3 = 9000 Wh = 9 kWh

Como queremos saber do custo em 1 mês, vamos multiplicar esse valor por 30, assim encontramos:

E_el= 9 . 30 = 270 kWh

Finalmente, para encontrar o valor em reais, basta multiplicar o valor encontrado por 0,40, então:

Valor = 270 . 0,4 = 108

Assim, custo do aquecedor ao final de 1 mês será de 108 reais.

Para saber mais, leia também:

• Fórmulas de potência: quais são e exemplos
• Carga Elétrica
• Potencial Elétrico
• Eletrostática
• Circuito Elétrico
• Geradores Elétricos
• Leis de Kirchhoff
• Fórmulas de Física
• Resistência Elétrica

Exercícios Resolvidos

1) Enem - 2016

Um eletricista deve instalar um chuveiro que tem as especificações 220 V — 4 400 W a 6 800 W. Para a instalação de chuveiros, recomenda-se uma rede própria, com fios de diâmetro adequado e um disjuntor dimensionado à potência e à corrente elétrica previstas, com uma margem de tolerância próxima de 10%. Os disjuntores são dispositivos de segurança utilizados para proteger as instalações elétricas de curtos-circuitos e sobrecargas elétricas e devem desarmar sempre que houver passagem de corrente elétrica superior à permitida no dispositivo. Para fazer uma instalação segura desse chuveiro, o valor da corrente máxima do disjuntor deve ser

a) 20 A
b) 25 A
c) 30 A
d) 35 A
e) 40 A

2) Enem - 2016

Uma lâmpada LED (diodo emissor de luz), que funciona com 12 V e corrente contínua de 0,45 A, produz a mesma quantidade de luz que uma lâmpada incandescente de 60 W de potência. Qual é o valor da redução da potência consumida ao se substituir a lâmpada incandescente pela de LED?

a) 54,6 W
b) 27,0 W
c) 26,6 W
d) 5,4 W
e) 5,0 W

3) Enem - 2017

No manual fornecido pelo fabricante de uma ducha elétrica de 220 V é apresentado um gráfico com a variação da temperatura da água em função da vazão para três condições (morno, quente e superquente). Na condição superquente, a potência dissipada é de 6500 W.

Considere o calor específico da água igual a 4200 J/(kg.ºC) e a densidade da água igual a 1 kg/L.

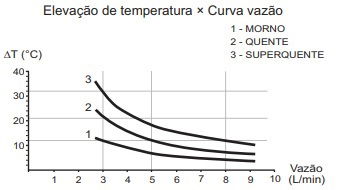
Com base nas informações dadas, a potência na condição morno corresponde a que fração da potência na condição superquente?

a) 1/3
b) 1/5
c) 3/5
d) 3/8
e) 5/8

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.