Potencial Elétrico
O potencial elétrico ou potencial eletrostático de um ponto em relação a um ponto de referência, é definido pelo trabalho da força elétrica sobre uma carga eletrizada no deslocamento entre esses dois pontos.
Sendo uma grandeza escalar, necessita apenas, para ficar totalmente definida, da intensidade e de uma unidade de medida. Portanto, não requer nem direção, nem sentido.
Fórmula
O potencial de um ponto pertencente a um campo elétrico é encontrado dividindo-se o trabalho pelo valor da carga. Esse valor é sempre medido em relação a um ponto de referência.
Ao se definir um ponto de referência, convenciona-se que o potencial neste ponto é nulo.
Assim, a fórmula para o cálculo do potencial elétrico é dado por:
Onde:
VA: Potencial elétrico do ponto A (V)
TAB: Trabalho da força elétrica ao deslocar a carga do ponto A ao ponto B (J)
q: Carga elétrica (C)
No Sistema Internacional de Unidade (SI) o potencial elétrico é medido em Volts (Joule/Coulomb) em homenagem ao físico italiano Alessandro Volta (1745-1827), criador da pilha elétrica.
Diferença de Potencial
A diferença de potencial (ddp), também chamada de tensão elétrica ou voltagem, é uma importante grandeza no estudo dos fenômenos elétricos.
No cotidiano, usa-se mais o conceito de diferença de potencial do que o de potencial elétrico de um ponto. Por exemplo, nos aparelhos elétricos, normalmente aparece a indicação da sua voltagem.

Quando dizemos que existe uma alta voltagem entre dois pontos, significa que a carga recebe uma grande quantidade de energia no seu deslocamento.
A diferença de potencial é indicada por:
U = VA - VB
U: diferença de potencial (V)
VA: potencial elétrico em um ponto A (V)
VB: potencial elétrico em um ponto B (V)
Exemplo
Uma carga elétrica de pequenas dimensões e com intensidade de 4.10-6 C é transportada de um ponto A para um ponto B de um campo elétrico. O trabalho realizado pela força elétrica que age sobre a carga tem intensidade de 3.10-4 J. Determine:
a) O potencial elétrico do ponto A, considerando o ponto B como ponto de referência.
b) A diferença de potencial entre os pontos A e B.
Solução:
a) Considerando o ponto B como ponto de referência, temos:
b) A diferença de potencial é calculada considerando o potencial nos pontos A e B. Como o ponto B foi definido como ponto de referência, então VB=0. Sendo assim, temos:
U = VA - VB
U = 75 - 0 = 75 V
Potencial Elétrico no Campo de uma Carga
Quando um campo elétrico é gerado por uma carga fixa no vácuo, a diferença de potencial pode ser calculada como sendo:
Onde,
U: diferença de potencial (V)
k0: constante eletrostática no vácuo (9.109 N.m2/C2)
Q: carga elétrica fixa (C)
dA: distância da carga fixa ao ponto A (m)
dB: distância da carga fixa ao ponto B (m)
Se considerarmos o ponto B infinitamente afastado da carga Q (VB = 0), então teremos que o potencial no ponto A será dado por:
Sendo,
VA: potencial do ponto A (V)
k0: constante eletrostática no vácuo (9.109 N.m2/C2)
Q: carga elétrica fixa (C)
dA: distância da carga fixa ao ponto A (m)
Para calcular o potencial elétrico resultante de um sistema de cargas, basta calcular o valor do potencial de cada carga no campo elétrico e depois somá-los.
Exemplo
Uma carga puntiforme de 2.10-8 C, está fixa no vácuo e gera um campo elétrico a sua volta. Qual o potencial elétrico de um ponto situado a uma distância de 60 cm desta carga? Considere k0 = 9.109 N.m2/C2 e adote como referencial o infinito.
Solução:
Para calcular o potencial no ponto dado, basta substituir na fórmula. Contudo, devemos ter atenção as unidades, pois a unidade da distância não está no sistema internacional. Então, primeiro devemos fazer a mudança de unidade:
d = 60 cm = 0,6 m
Substituindo:
Superfície Equipotencial
Numa superfície equipotencial todos os pontos apresentam um valor constante para o potencial elétrico.
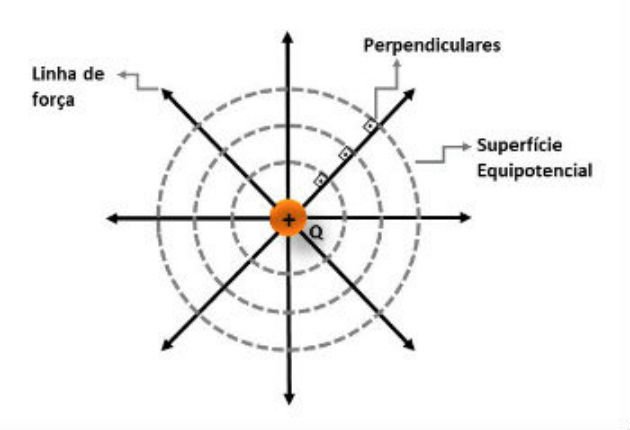
Em um campo elétrico gerado por uma carga puntiforme, as superfícies equipotenciais serão esferas concêntricas, ou seja, apresentam um mesmo ponto central.
A carga puntiforme situa-se no centro dessas esferas e as linhas de força são perpendiculares as superfícies equipotenciais.
Na figura abaixo representamos uma carga Q, carregada positivamente. Indicamos ainda as linhas de força e as superfícies equipotenciais.
Energia Potencial Elétrica
A energia potencial elétrica está associada ao trabalho da força elétricas dentro de um campo elétrico.
Para uma carga puntual fixa, a energia potencial elétrica, medida em Joule (J), é expressa pela seguinte fórmula:
Sendo:
Ep: energia potencial elétrica (J)
K: constante elétrica do meio (N.m2/C2). No vácuo, seu valor é de 9.109 N.m2/C2.
Q: carga fixa (C)
q: carga de prova (C)
d: distância entre as cargas (m)
Para saber mais, leia também:
- Eletrostática
- Lei de Coulomb
- Carga Elétrica
- Processos de Eletrização
- Resistência Elétrica
- Corrente Elétrica
- Leis de Kirchhoff
Exercícios Resolvidos
1) Num campo elétrico, uma carga de 2C é levada de um ponto X a um ponto Y muito afastado, tendo as forças elétricas um trabalho de 100 J. Determine o potencial elétrico no ponto x:
2) Determine o trabalho de uma carga elétrica colocada em um ponto A cujo potencial elétrico é 2.104 V, sendo o valor da carga igual a - 6 μC.
Pratique com Exercícios sobre potencial elétrico.
Leia também
GOUVEIA, Rosimar. Potencial Elétrico. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/potencial-eletrico/. Acesso em:


