Quadrado Perfeito

Rafael C. Asth

Professor de Matemática e Física

Um quadrado perfeito ou número quadrado perfeito é um número natural que se radicado, possui como resultado outro número natural.

Ou seja, são resultados da operação de um número multiplicado por ele mesmo.

Exemplo:

1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
(...)

A fórmula do quadrado perfeito é representada por: n × n = a ou n² = a. Desse modo, n é um número natural e a é um número quadrado perfeito.

O que são os números quadrados perfeitos?

A definição de um número quadrado perfeito pode ser entendida como: um número natural (inteiro positivo) cuja raiz quadrada é, também, um número natural (inteiro positivo).

Em outras palavras, é um número que, ao extrair a raiz quadrada, o resultado é exato.

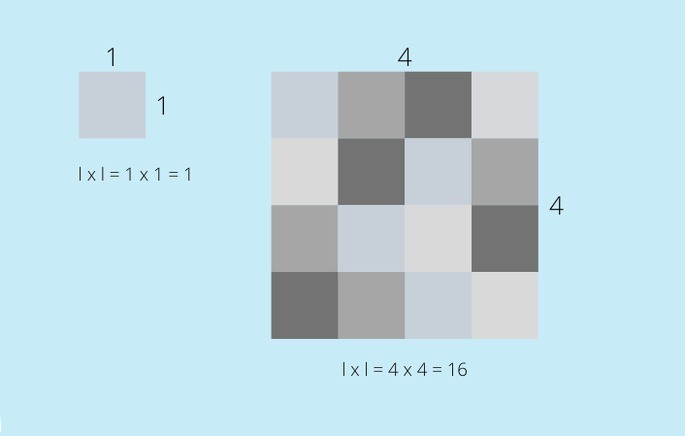
Assim temos: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100...

√1 = 1, √4 = 2, √9 = 3, √16 = 4, √25 = 5, √36 =6, √49 = 7, √64 = 8, √81 = 9, √100 = 10...

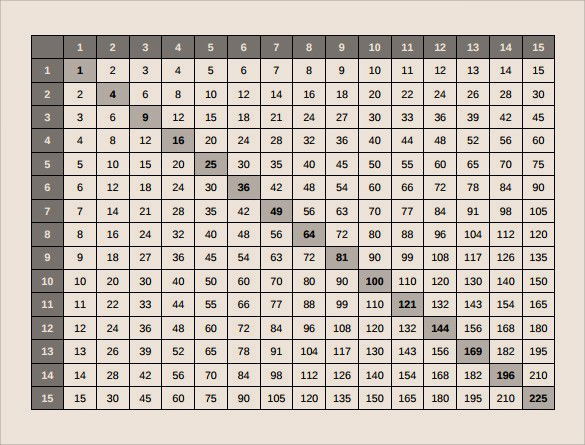
Quadrados Perfeitos — Tabela de multiplicação e sinalização dos números quadrados perfeitos até 15

Se tomarmos a geometria como base, podemos pensar que um quadrado é a figura que possui os lados com a mesma medida.

Assim, a área do quadrado é L × L ou L².

Todo quadrado cujos lados forem números inteiros, serão quadrados perfeitos.

Como saber se um número é um quadrado perfeito?

Se ele possui uma raiz quadrada exata, a partir da fatoração de um número e, caso ele seja o resultado do quadrado de outros números, podemos dizer que é um quadrado perfeito.

Exemplo:
2 704 é um quadrado perfeito?

Para responder à pergunta é preciso fatorar 2 704.

Daí, temos: 2 704 = 2 × 2 × 2 × 2 × 13 × 13 = 2⁴ × 13^{2 .}

^{Outra forma de escrever é organizando as potências na forma de quadrados.}

^{$2 espaço 704 espaço igual a espaço 2 espaço. espaço 2 espaço. espaço 2 espaço. espaço 2 espaço. espaço 13 espaço. espaço 13 2 espaço 704 espaço igual a 2 ao quadrado espaço. espaço 2 ao quadrado espaço. espaço 13 ao quadrado 2 espaço 704 espaço igual a parêntese esquerdo 2 espaço. espaço 2 espaço. espaço 13 parêntese direito ao quadrado 2 espaço 704 espaço igual a 52 ao quadrado$}

2 704 é o número quadrado perfeito de 52.

Portanto, a raiz quadrada de 2 704 é 52.

Regras do quadrado perfeito

Um número quadrado perfeito é aquele que possui uma raiz exata.
Um número quadrado perfeito ímpar possui sua raiz ímpar e um par possui uma raiz par.
Números quadrados perfeitos nunca terminam com os algarismos 2, 3, 7 e 8.
Números terminados em 0 possuem quadrados terminados em 00.
Números terminados em 1 ou 9 possuem quadrados terminados em 1.
Números terminados em 2 ou 8 possuem quadrados terminados em 4.
Números terminados em 3 ou 7 possuem quadrados terminados em 9.
Números terminados em 4 ou 6 possuem quadrados terminados em 6.
Números terminados em 5 possuem quadrados terminados em 25

Outras relações

O quadrado de um número é igual ao produto de seus adjacentes mais um. Por exemplo: o quadrado de sete (7²) é igual ao produto de seus números adjacentes (6 e 8) mais 1. Desta forma: 7² = 6 × 8 + 1 = 48 + 1 = 49.

$reto x ao quadrado igual a parêntese esquerdo reto x menos 1 parêntese direito espaço. espaço parêntese esquerdo reto x mais 1 parêntese direito espaço mais espaço 1$

Os quadrados perfeitos são resultados de uma sucessão matemática entre o quadrado perfeito anterior e uma progressão aritmética.

1² = 1
2² = 1 + 3 = 4
3² = 4 + 5 = 9
4² = 9 + 7 = 16
5² = 16 + 9 = 25
6² = 25 + 11 = 36
7² = 36 + 13 = 49
8² = 49 + 15 = 64
9² = 64 + 17 = 81
10² = 81 + 19 = 100...

Veja Também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.