Resistores: o que são, associações e leis de Ohm
Um resistor é um componente eletrônico projetado para limitar ou controlar a corrente elétrica que passa por um circuito.
Os resistores são componentes que se opõem a passagem de corrente elétrica, ou seja, “resistem” a passagem de corrente elétrica, limitando sua intensidade.
Também chamados de resistências, convertem energia elétrica em calor, conforme o material resistivo de que são feitos. Estão presentes em aparelhos como chuveiros, televisores, computadores, aquecedores, rádios, lâmpadas incandescentes, dentre outros.
São representados pela letra R e no Sistema Internacional de Unidades (SI) são medidos em Ohm (Ω), ou seja, Volts (V) / Ampére (A).
Resistores têm diversas aplicações em circuitos elétricos, tais como:
- Limitar a corrente: protegem componentes sensíveis, como LEDs, de correntes excessivas.
- Divisores de tensão: utilizados para reduzir a tensão em uma parte do circuito.
- Dissipação de energia: convertendo energia elétrica em calor.
Tipos de Resistores
Há dois tipos de resistores, fixos e variáveis. Os resistores fixos são constituídos de filme carbono, filme metálico, fio de precisão, dentre outros.
Os resistores variáveis podem ser ajustados manualmente. São exemplos potenciômetros, LDR (light depend resistor), PTC (coeficiente de temperatura positivo), NTC (coeficiente de temperatura negativo), Magnetorresistores, reostato, dentre outros.
Associação de Resistores
Nos circuitos elétricos há uma quantidade de resistores que se organizam em série ou em paralelo. Note que o chamado “resistor equivalente” (Req) representa a resistência total dos resistores associados.
Associação de resistores em série
Na associação em série, o resistor equivalente será igual à soma de todas as resistências presentes no circuito.
A corrente elétrica (i) é a mesma para todos os resistores do circuito. Para calcular o valor do resistor equivalente, utiliza-se a seguinte expressão:
.
Exemplo:
Em uma associação de resistores em série, R1 = 10Ω, R2 = 15Ω e R3 = 20Ω. Determine a resistência equivalente.
Resolução:
Para o cálculo, basta somar os valores dos resistores.
Associação de resistores em paralelo
Na associação em paralelo, a corrente elétrica se divide entre eles. Assim, a corrente total que passa pelo circuito é igual à soma das correntes elétricas que passam por cada um dos resistores da associação.
Dessa forma, a resistência equivalente (Req) dos resistores associados em paralelo, será menor que o resistor de menor resistência da associação, sendo calculado pela seguinte fórmula:
Exemplo:
Em uma associação de resistores em paralelo, R1 = 10Ω, R2 = 15Ω e R3 = 20Ω. Determine a resistência equivalente.
Resolução:
Substituindo os valores na fórmula:
Igualando os denominadores:
Associação de resistores mista
Nesse tipo de associação, os resistores se encontram associados em série e em paralelo. Dessa forma, para calcular a resistência do circuito, deve-se calcular o valor total dos resistores associados em paralelo, somá-los aos resistores em série, para assim, obter o resultado.
Leis de Ohm e resistência elétrica
A resistência elétrica foi descoberta pelo físico alemão Georg Simon Ohm (1787-1854), em 1827. Ele postulou as duas que determinam a resistência elétrica dos condutores.
A resistência de um material depende de:
- O tipo de material (condutor ou isolante)
- O comprimento e a área da seção transversal do material
- A temperatura
Primeira Lei de Ohm
A primeira Lei de Ohm postula que em um condutor ôhmico (resistência constante), mantido à temperatura constante, a intensidade de corrente elétrica será proporcional à diferença de potencial aplicada entre suas extremidades, ou seja, sua resistência elétrica é constante.
É representada pela seguinte fórmula:
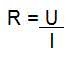ou 
donde:
R: resistência, medida em Ohm (Ω)
U: diferença de potencial elétrico (ddp), medido em Volts (V)
I: intensidade da corrente elétrica, medida em Ampére (A).
Exemplo:
Um resistor de 100 Ω é conectado a uma fonte de tensão de 12 V. Qual é a corrente que passa pelo resistor?
Resolução:
Substituindo os valores na fórmula e resolvendo para i:
Segunda lei de Ohm
A segunda lei de Ohm estabelece que a resistência elétrica de um material é diretamente proporcional ao seu comprimento e inversamente proporcional à sua área de secção transversal representada pela seguinte fórmula:
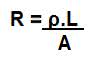
donde:
ρ: resistividade do condutor (depende do material e de sua temperatura);
R: resistência;
L: comprimento;
A: área de secção.
Exemplo:
Um fio de cobre tem comprimento L = 2 m e área de seção transversal de 1 mm². Sabendo que a resistividade do cobre é 
, calcule a resistência elétrica desse fio.
Resolução:
É necessário que as unidades estejam iguais, assim, 1 mm² = 
m².
Substituindo os valores na fórmula:
Veja mais sobre as leis de Ohm.
Exercícios sobre resistores resolvidos
Exercício 1
Dois resistores de 8 Ω e 12 Ω são conectados em série. Qual é a resistência equivalente?
a) 15 Ω
b) 20 Ω
c) 25 Ω
d) 30 Ω
e) 30 Ω
Como os resistores estão em série, basta adicionar seus valores, conforme a fórmula:
Exercício 2
Dois resistores de 6 Ω e 4Ω são conectados em paralelo. Qual é a resistência equivalente?
a) 1,5 Ω
b) 2,4 Ω
c) 9,2 Ω
d) 10,5 Ω
e) 12,8 Ω
Substituindo os valores na fórmula para o cálculo:
Multiplicamos cruzado os termos da proporção:
Exercício 3
Qual será a corrente que passa por um resistor de 50 Ω, quando ele é conectado a uma fonte de 10 V?
a) 0,1 A
b) 0,2 A
c) 0,3 A
d) 0,5 A
e) 0,6 A
A equação que relaciona resistência, corrente e tensão é a primeira lei de Ohm.
Leia também:
- Associação de Resistores
- Resistência Elétrica
- Exercícios sobre Lei de Ohm com respostas
- Potência Elétrica
- Fórmulas de Física
- Leis de Kirchhoff
- Efeito Joule
Referências Bibliográficas
Ramalho, F.; Nicolau, G.; Toledo, P. Os Fundamentos da Física, 3. ed. São Paulo: Moderna, 2013.
ASTH, Rafael. Resistores: o que são, associações e leis de Ohm. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/resistores/. Acesso em:
