Segunda Lei de Newton

Rosimar Gouveia

Professora de Matemática e Física

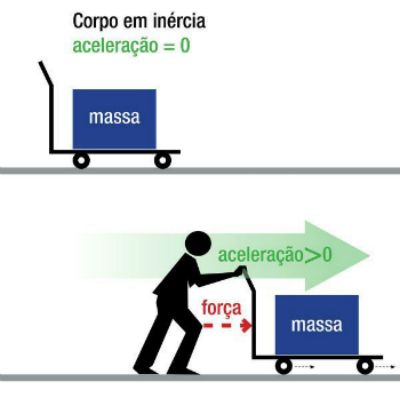
A Segunda Lei de Newton estabelece que a aceleração adquirida por um corpo é diretamente proporcional a resultante das forças que atuam sobre ele.

Como a aceleração representa a variação de velocidade por unidade de tempo, a 2ª Lei indica que as forças são os agentes que produzem as variações de velocidade em um corpo.

Também chamada de princípio fundamental da Dinâmica, foi concebida por Isaac Newton e forma, junto com outras duas leis (1ª Lei e Ação e Reação), os fundamentos da Mecânica Clássica.

Fórmula

Representamos matematicamente a Segunda Lei como:

Onde,

Força e aceleração são grandezas vetoriais, por isso estão representadas com uma seta sobre as letras que as indicam.

Sendo grandezas vetoriais, elas necessitam, para ficarem totalmente definidas, de um valor numérico, de uma unidade de medida, de uma direção e de um sentido. A direção e o sentido da aceleração será o mesmo da força resultante.

Na 2ª Lei, a massa do objeto (m) é a constante de proporcionalidade da equação e é a medida da inércia de um corpo.

Desta forma, se aplicarmos a mesma força em dois corpos com massas diferentes, o de maior massa sofrerá uma menor aceleração. Daí concluímos que o de maior massa resiste mais as variações de velocidade, logo tem maior inércia.

Exemplo:

Um corpo de massa igual a 15 kg move-se com aceleração de módulo igual a 3 m/s². Qual o módulo da força resultante que atua no corpo?

O módulo da força será encontrado aplicando-se a 2ª lei, assim temos:

F_R = 15 . 3 = 45 N

Aprenda mais sobre força resultante.

As Três Leis de Newton

O físico e matemático Isaac Newton (1643-1727) formulou as leis básicas da Mecânica, onde descreve os movimentos e suas causas. As três leis foram publicadas em 1687, na obra "Princípios Matemáticos da Filosofia Natural".

Primeira Lei de Newton

Newton se baseou nas ideias de Galileu sobre a inércia para formular a 1ª Lei, por isso, é também chamada de Lei da Inércia e pode ser enunciada:

Na ausência de forças, um corpo em repouso continua em repouso e um corpo em movimento move-se em linha reta, com velocidade constante.

Em resumo, a Primeira Lei de Newton indica que um objeto não pode iniciar um movimento, parar ou mudar de direção por si, somente. É preciso a ação de uma força para provocar alterações em seu estado de repouso ou movimento.

Terceira Lei de Newton

A Terceira Lei de Newton é a Lei da "Ação e Reação". Isso significa que, para cada ação, há uma reação de mesma intensidade, mesma direção e em sentido oposto. O princípio da ação e reação analisa as interações que ocorrem entre dois corpos.

Quando um corpo sofre a ação de uma força um outro receberá a sua reação. Como o par ação-reação ocorre em corpos diferentes, as forças não se equilibram.

Saiba mais em:

• Três Leis de Newton
• Gravidade
• O que é a Inércia na Física?
• Fórmulas de Física
• Quantidade de Movimento
• Plano inclinado

Exercícios Resolvidos

1) UFRJ-2006

Um bloco de massa m é abaixado e levantado por meio de um fio ideal. Inicialmente, o bloco é abaixado com aceleração constante vertical, para baixo, de módulo a (por hipótese, menor do que o módulo g da aceleração da gravidade), como mostra a figura 1. Em seguida, o bloco é levantado com aceleração constante vertical, para cima, também de módulo a, como mostra a figura 2. Sejam T a tensão do fio na descida e T’ a tensão do fio na subida.

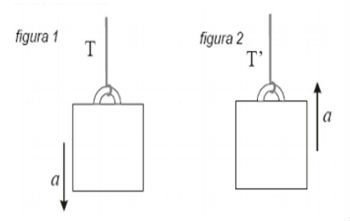
Determine a razão T’/T em função de a e g.

2) Mackenzie-2005

Um corpo de 4,0kg está sendo levantado por meio de um fio que suporta tração máxima de 50N. Adotando g = 10m/s², a maior aceleração vertical que é possível imprimir ao corpo, puxando-o por esse fio, é:

a) 2,5m/s²
b) 2,0m/s²
c) 1,5m/s²
d) 1,0m/s²
e) 0,5m/s²

3) PUC/MG-2007

Na figura, o bloco A tem uma massa m_A = 80 kg e o bloco B, uma massa m_B = 20 kg. São ainda desprezíveis os atritos e as inércias do fio e da polia e considera-se g = 10m/s² .

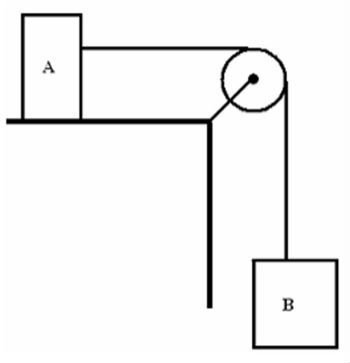
Sobre a aceleração do bloco B, pode-se afirmar que ela será de:

a) 10 m/s² para baixo.
b) 4,0 m/s² para cima.
c) 4,0 m/s² para baixo.
d) 2,0 m/s² para baixo.

4) Fatec-2006

Dois blocos A e B de massas 10 kg e 20 kg, respectivamente, unidos por um fio de massa desprezível, estão em repouso sobre um plano horizontal sem atrito. Uma força, também horizontal, de intensidade F = 60N é aplicada no bloco B, conforme mostra a figura.

O módulo da força de tração no fio que une os dois blocos, em newtons, vale

a) 60
b) 50
c) 40
d) 30
e) 20

5) ITA-1996

Fazendo compras num supermercado, um estudante utiliza dois carrinhos. Empurra o primeiro, de massa m, com uma força F, horizontal, o qual, por sua vez, empurra outro de massa M sobre um assoalho plano e horizontal. Se o atrito entre os carrinhos e o assoalho puder ser desprezado, pode-se afirmar que a força que está aplicada sobre o segundo carrinho é:

a) F
b) MF/ (m + M)
c) F (m + M) / M
d) F / 2
e) outra expressão diferente

Veja mais:

• Exercícios de Física (resolvidos) para 1º ano do ensino médio
• Exercícios sobre força de tração
• Exercícios sobre a segunda lei de newton (com respostas explicadas)

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.