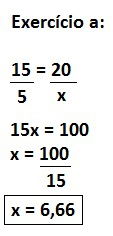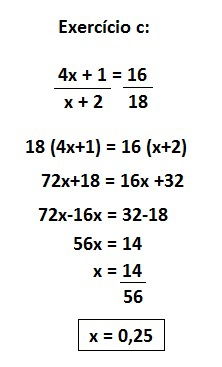Teorema de Tales

Rafael C. Asth

Professor de Matemática e Física

O Teorema de Tales é uma teoria aplicada na Geometria e expressa pelo enunciado:

"A intersecção de um feixe de retas paralelas por duas retas transversais forma segmentos proporcionais."

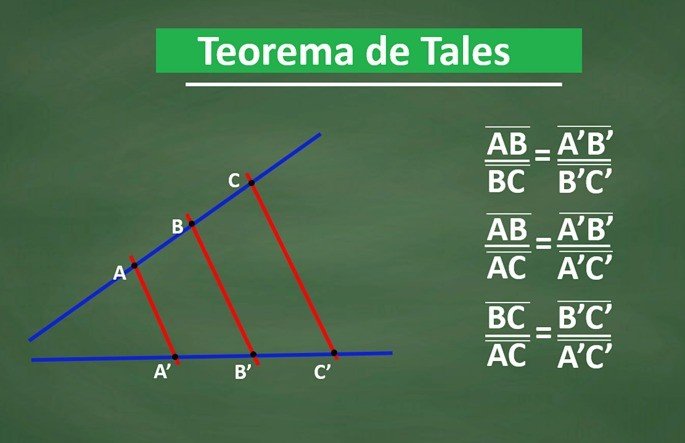
Fórmula do teorema de Tales

Para compreender melhor o teorema de tales, observe a figura abaixo:

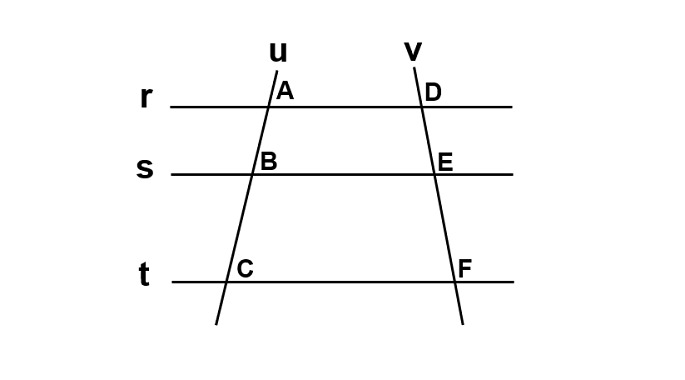
Na figura acima as retas transversais u e v interceptam as retas paralelas r, s e t. Os pontos pertencentes na reta u são: A, B e C; e na reta v, os pontos: D, E e F. Logo, de acordo com o Teorema de Tales:

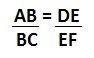
Lê-se: AB está para BC, assim como DE está para EF.

Exemplo: determine a medida de x indicada na imagem.

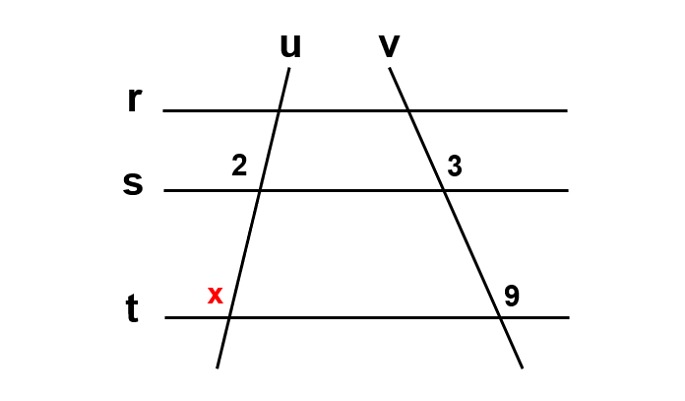
Aplicando o teorema de Tales, temos:

Teorema de Tales nos triângulos

O teorema de Tales também é aplicado em situações que envolvem triângulos. Veja abaixo um exemplo em que se aplica o teorema:

De acordo com a semelhança de triângulos podemos afirmar que: o triângulo ABC é semelhante ao triângulo AED. É representado da seguinte forma:

Δ ABC ~ Δ AED

Exemplo: determine a medida x indicada na imagem.

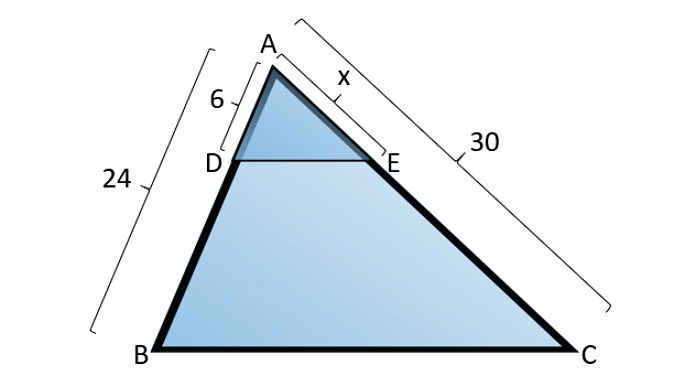
Aplicando o teorema de Tales, temos:

Como foi descoberto o teorema de Tales?

O teorema foi desenvolvido pelo filósofo, astrônomo e matemático grego Tales de Mileto (624 a.C.- 558 a.C.) e, por isso, recebe esse nome.

O experimento de Tales foi realizado através da observação de uma sombra da pirâmide. A partir disso, ele conseguiu calcular a altura da pirâmide Quéops, no Egito, com base na sombra que ela projetava.

Considerado o “Pai da Geometria Descritiva”, Tales contribuiu para o avanço dos estudos de razão e proporção, que até os dias de hoje são utilizados para calcular distâncias.

Saiba mais lendo sobre razão e proporção.

Exercícios resolvidos sobre o Teorema de Tales

Determine o valor de x nas figuras abaixo:

Questão 1

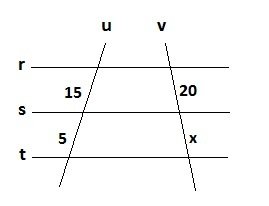
Questão 2

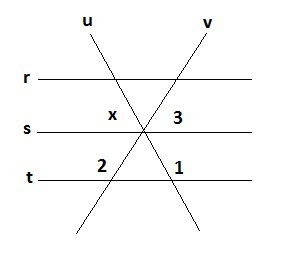
Questão 3

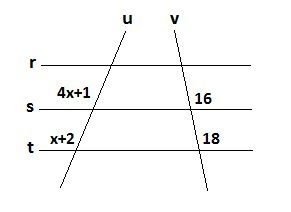
Saiba mais sobre o matemático Tales de Mileto e aproveite Teorema de Tales - Exercícios para aprofundar seus conhecimentos.

Estude mais com Exercícios sobre retas paralelas cortadas por uma transversal.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.