Teste de raciocínio lógico (com respostas e pontuação)
A lógica está presente nas ciências, tecnologias e problemas do dia a dia, além de compor avaliações de processos seletivos em empresas e concursos.
Você tem até 30 min para solucionar as questões, simulando uma avaliação real. No final, confira seu desempenho.
Bom teste!
Atenção às regras do simulado
- 1010 questões
- Duração máxima de 30min
- Seu resultado e o gabarito ficarão disponíveis ao finalizar o simulado
Questão 1
Em um edifício comercial, há sete escritórios para serem alugados, todos no mesmo lado de um corredor. De quantos modos diferentes, três estarão abertos e quatro fechados?
Existem 7 possibilidades para o primeiro, 6 para o segundo, 5 para o terceiro e sucessivamente.
7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040
No entanto, há a restrição de que 3 estejam abertos e 4 fechados. Como não há diferenciação entre os fechados e abertos, pode-se considerá-los como elementos repetidos.
Há 3 x 2 x 1 = 6 modos de organizar os abertos e 4 x 3 x 2 x 1 = 24 modos de organizar os fechados.
É uma permutação de elementos repetidos, onde o número total (5040), dever ser dividido pelo produto entre 6 e 24.
Assim, o número de possibilidades para organizar os sete escritórios, de modo que 3 estejam abertos e 4 fechados, é 35.
Questão 2
Nasci 11 anos depois do meu irmão. Nossa mãe, que está com 39 anos, é seis anos mais nova que meu pai. Se o primeiro filho do meu pai nasceu em seu aniversário de 26 anos, atualmente tenho
Se nasci 11 anos depois do meu irmão, ele é 11 anos mais velho que eu. Assim:
- Minha idade = idade do meu irmão menos 11.
Se meu pai é 6 anos mais velho que minha mãe, sua idade é:
- Idade do meu pai = 39 + 6 = 45.
Se meu irmão nasceu no mesmo dia que meu pai fez 26 anos, a idade atual do meu irmão é:
- Idade do meu irmão = 45 - 26 = 19.
Logo, a minha idade é:
- Idade do meu irmão menos 11.
19 - 11 = 8
Minha idade atual é 8 anos.
Questão 3
Um concurso foi realizado em uma escola com turmas do 1º ano do ensino fundamental ao 3° do ensino médio. A probabilidade de um aluno do 1° ano do médio ser sorteado é 1/4, um aluno do 2° do médio, 1/6, e um aluno do 3° do médio, 1/5. Sabendo que há nove séries no ensino fundamental, a probabilidade mais próxima de que o aluno sorteado seja do ensino fundamental é
O modo mais rápido e prático de descobrir a probabilidade de um aluno do fundamental ser sorteado é subtraindo a probabilidade de um aluno ser do médio, ou seja, calculando a probabilidade do evento complementar ocorrer.
P(aluno do fundamental ser sorteado) = P(aluno da escola ser sorteado) - P(aluno do médio ser sorteado)
Podemos afirmar esta declaração, pois todo aluno da escola é do fundamental ou do médio.
A probabilidade de um aluno da escola ser sorteado é 1, ou 100%.
A probabilidade de um aluno do médio ser sorteado é:
O Mínimo Múltiplo Comum entre 4, 6 e 5 é 60.
Deste modo, temos:
Dividindo 37 por 60, temos, aproximadamente, 0,616. Multiplicando por 100, 61,6%.
Voltando a relação de que:
P(aluno do fundamental ser sorteado) = P(aluno da escola ser sorteado) - P(aluno do médio ser sorteado)
P(aluno do fundamental ser sorteado) = 100% - 61,6% = 38,4%
Questão 4
Um dos três princípios fundamentais que compõem o pensamento lógico é o do terceiro excluído, que diz que uma declaração só pode assumir o valor verdadeiro ou falso, nenhum outro. Desta forma, pode-se classificar como uma proposição lógica a seguinte opção:
Apenas orações que podem assumir valores lógicos de verdadeiro ou falso são proposições. É preciso também que haja um verbo, sujeito e predicado.
Exclamações, interrogações e frases imperativas não podem ser proposições.
Questão 5
Considere que a seguinte afirmação seja falsa.
Se João vai à praia, então gosta de comprar na feira.
É correto afirmar que
A declaração é uma proposição composta, formada pelas simples:
- "João vai à praia"
- "gosta de comprar na feira."
Segundo a lógica clássica, a estrutura: se... então..., é um conectivo lógico condicional e só assume valor falso quando a segunda proposição simples é falsa e a primeira é verdadeira.
Deste modo, temos:
- "João vai à praia" (VERDADE)
- "gosta de comprar na feira." (FALSO)
Portanto:
Vai à praia e não gosta de comprar na feira.
Questão 6
Considere as afirmações:
I. Todo crocodilo é um réptil.
II. Todo réptil é um animal.
III. Todo animal é um ser vivo.
Deste modo, é correta a afirmação:
Uma boa maneira de organizar as informações é utilizando diagramas.
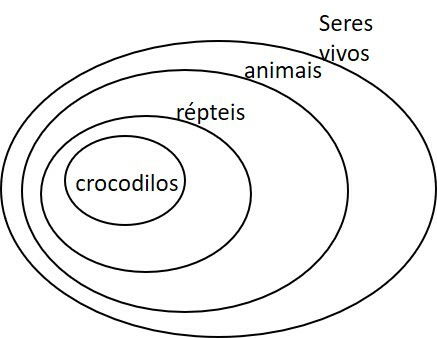
a) FALSO. Nem todo animal é réptil.
b) FALSO. Todo crocodilo é um réptil.
c) FALSO. Todo crocodilo é um réptil.
d) VERDADEIRO. Todo animal é um ser vivo e há répteis que não são crocodilos.
Questão 7
Considere falsa a seguinte declaração:
Se hoje é um dia ensolarado, então os pássaros cantam.
Deste modo, na declaração seguinte:
Hoje é um dia de verão se, e somente se, os pássaros não cantam.
Os valores lógicos de "Hoje é um dia de verão" e "os pássaros não cantam", para que a segunda declaração seja verdadeira, devem ser, respectivamente:
Este é um problema de lógica clássica onde a primeira declaração é uma proposição composta, formada pelas simples:
- "hoje é um dia ensolarado"
- "os pássaros cantam"
O conectivo da frase é a estrutura: "Se ... então ...", conhecida como condicional. Nesta estrutura, a única combinação que a torna falsa é quando a segunda é falsa e a primeira é verdadeira. Deste modo, temos:
- "hoje é um dia ensolarado" (VERDADEIRO)
- "os pássaros cantam" (FALSO)
A segunda declaração também é uma proposição composta, formada pelas simples:
- "Hoje é um dia de verão"
- "os pássaros não cantam"
O conectivo é o "se, somente se", conhecido como bicondicional. Esta proposição composta só assume o valor verdadeiro se ambas as simples forem verdadeiras ou se ambas forem falsas.
Como a primeira declaração, "os pássaros cantam", é falsa, a segunda, "os pássaros não cantam", só pode ser verdadeira, pois é a negação da primeira.
Deste modo, a única opção para que a segunda declaração seja verdadeira é que os valores das duas proposições simples sejam verdadeiras. Logo:
- "Hoje é um dia de verão" (VERDADEIRO)
- "os pássaros não cantam" (VERDADEIRO)
Questão 8
A seguinte sequência numérica segue um determinado padrão.
... , 18, 9, 54, 27, 162, ...
Desta forma, obedecendo às mesmas leis que a criaram, o número que antecede o 18 e o número que sucede o 162 são, respectivamente:
Do elemento 18 para o 9 houve uma redução que pode ter sido através de uma subtração por 9 ou uma divisão por 2.
Do nove para o 54 houve um aumento, que pode ter se dado por uma soma de 45 unidades ou uma multiplicação por 6.
Testando a primeira hipótese, subtraindo 9 unidades de 54, não obtemos 27, no entanto, ao dividir por 2, sim.
Seguindo a segunda hipótese, ao multiplicar 27 por 6, obtemos 162 e, ao dividir por 2, temos 81.
Já no início da sequência, o número que multiplica por 6 e resulta em 18 é o 3.
Assim, o antecessor do 18 é 3 e o sucessor do 27 é 81.
Questão 9
Observe a seguinte sequência de formas geométricas que segue um padrão.
![]()
Da esquerda para a direita, o sétimo elemento é o triângulo novamente e, assim, a sequência continua a se repetir. Pode-se afirmar que o 117º elemento desta sequência é da cor
Como a sequência se repete a cada seis elementos, procuramos o múltiplo mais próximo de 117. Para isto realizamos a divisão de 117 por 6:
Isto significa que há 19 sequências inteiras se repetindo e mais três elementos. Visto que a sequência se desenvolve da esquerda para direita, basta contar mais três elementos.
O terceiro elemento é o pentágono amarelo.
Questão 10
Considere três conjuntos, A, B e C, respectivamente com 13, 17 e 19 elementos. Há 5 elementos comuns aos três conjuntos, 8 elementos estão exclusivamente no conjunto B, a intersecção entre A e B possui 8 elementos e entre A e C, 7 elementos. É possível afirmar que
Como há uma intersecção entre os três conjuntos, podemos representar a situação utilizando os diagramas:
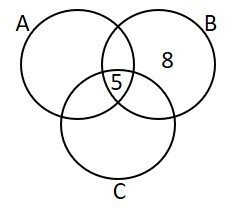
Segundo as informações no enunciado, temos:
- 5 elementos comuns aos três conjuntos;
- 8 elementos estão exclusivamente no conjunto B;
- 8 elementos simultaneamente em A e B;
- 7 elementos simultaneamente em A e C;
- 11 elementos estão exclusivamente no conjunto C.
Podemos preencher as duas primeiras informações no diagrama.
Como há 8 elementos entre A e B, devemos considerar que 5 já estão posicionados, faltando apenas 3. Da mesma forma, havendo 7 elementos entre A e C, falta acrescentar 2 na área comum entre eles.
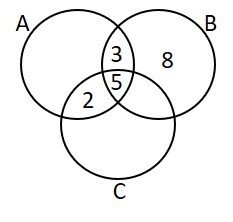
Com base nos totais de cada conjunto, A, B e C, respectivamente com 13, 17 e 19 elementos, podemos terminar de preencher o diagrama.
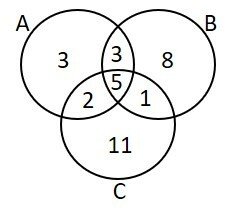
Diante disto, podemos verificar as opções.
a) FALSA. Embora no total há 8 elementos na intersecção entre A e B, 5 também pertencem a C.
b) FALSA. Para serem disjuntos, não podeira haver intersecção entre eles.
c) FALSA. O conjunto A possui 13 elementos. Pelo menos em mais de um conjunto incluem os elementos que estão em dois e três conjuntos.
Somando os elementos que estejam em mais de um conjunto: 2 + 1 + 3 + 5 = 11.
d) VERDADEIRA. A união entre os três conjuntos é a soma dos elementos em cada região.
5 + 3 + 1 + 2 + 8 + 11 + 3 = 33
ASTH, Rafael. Teste de raciocínio lógico (com respostas e pontuação). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/teste-de-raciocinio-logico/. Acesso em:


