Tipos de Matrizes: quais são, suas características

Os tipos de matrizes incluem as diversas maneiras de representação de seus elementos. São classificadas em: matriz linha, coluna, nula, quadrada, transposta, oposta, identidade, inversa e iguais.

Antes de mais nada, devemos atentar ao conceito de matriz. Trata-se de uma representação matemática que inclui em linhas (horizontais) e colunas (verticais): números, constantes, incógnitas, funções e outros elementos matemáticos.

Os objetos matemáticos que compõem a matriz são chamados de elementos, representados entre parênteses ou colchetes.

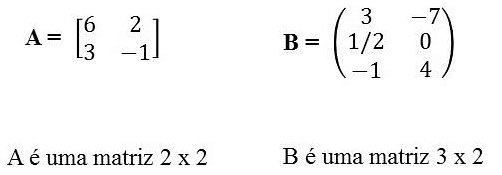
Classificação ou tipos das Matrizes

Matriz Linha

Formada por uma única linha, por exemplo:

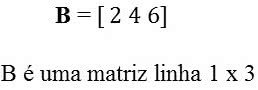
Matriz Coluna

Formada por uma única coluna, por exemplo:

Matriz Nula

Formada por elementos iguais a zero, por exemplo:

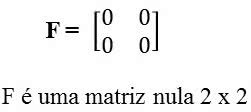
Matriz Quadrada

Formada pelo mesmo número de linhas e colunas, por exemplo:

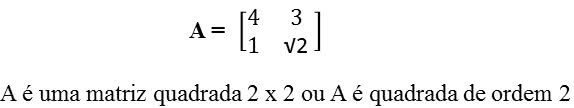
Matriz Transposta

A matriz transposta (indicada pela letra t) é aquela que apresenta os mesmos elementos de uma linha ou coluna comparada com outra matriz.

No entanto, os elementos iguais entre as duas são invertidos, ou seja, a linha de uma apresenta os mesmos elementos que a coluna de outra. Ou ainda, a coluna de uma possui os mesmos elementos da linha de outra.

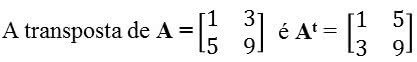
Matriz Oposta

Na matriz oposta, os elementos entre duas matrizes apresentam sinais diferentes, por exemplo:

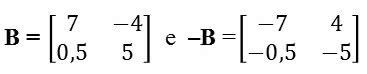
Matriz Identidade

A matriz identidade ocorre quando os elementos da diagonal principal são todos iguais a 1 e os outros elementos são iguais a 0 (zero):

Matriz Inversa

A matriz inversa é uma matriz quadrada. Ela ocorre quando o produto de duas matrizes for igual a uma matriz identidade quadrada de mesma ordem.

A . B = B . A = I_n (quando a matriz B é inversa da matriz A)

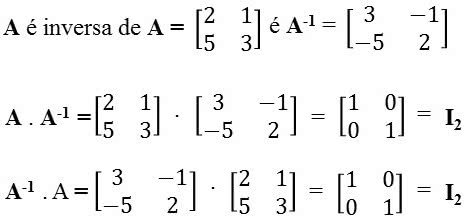
Obs: Para encontrar a matriz inversa utiliza-se multiplicar matrizes.

Matrizes iguais

Quando temos matrizes iguais, os elementos das linhas e das colunas são correspondentes:

Veja também: Matrizes

Exercícios de Matrizes

Exercício 1

(U.F. Uberlândia-MG) Sejam A, B e C matrizes quadradas de ordem 2, tais que A . B = I, em que I é a matriz identidade.
A matriz X tal qual A . X . A = C é igual a:

a) B . C . B
b) (A²) ^-1 . C
c) C . (A^-1)²
d) A . C . B

Exercício 2

(FGV-SP) A e B são matrizes e A^t é a transposta de A.

Se 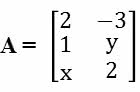e , e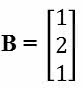ntão a matriz A^t . B será nula para:

a) x + y = - 3
b) x . y = 2
c) x/y = - 4
d) x . y² = - 1
e) y/x = - 8

Exercício 3

(U.F. Pelotas-RS) Cada elemento a_ij da matriz T indica o tempo, em minutos, que um semáforo fica aberto, num período de 2 minutos, para que haja fluxo de automóveis da rua i para a rua j, considerando que cada rua tenha mão dupla.

De acordo com a matriz, o semáforo que permite o fluxo de automóveis da via 2 para a 1 fica aberto durante 1,5 min de um período de 2 min.

Com base no texto e admitindo que é possível até 20 carros passarem por minuto cada vez que o semáforo se abre, é correto afirmar que, das 8h às 10h, considerando o fluxo indicado pela matriz T, o número máximo de automóveis que podem passar da rua 3 para a 1 é:

a) 300
b) 1200
c) 600
d) 2400
e) 360

Leia também os artigos:

• Matrizes - Exercícios
• 11 exercícios sobre multiplicação de matrizes
• Matrizes e Determinantes
• Multiplicação de Matrizes
• Regra de Cramer