Trabalho na Física (produzido por uma força)
O trabalho é uma grandeza física que representa a transferência de energia a um corpo devido à atuação de uma força que provoca seu deslocamento.
Embora tanto a força quanto o deslocamento sejam grandezas vetoriais, o trabalho é uma grandeza escalar, ou seja, é completamente definido por um valor numérico e sua unidade de medida.
O trabalho é calculado como o produto da força aplicada (N), do deslocamento do objeto (m) e do cosseno do ângulo entre a direção da força e a do deslocamento.
No Sistema Internacional de Unidades (SI), a unidade de medida do trabalho é o newton-metro (N·m), que recebe o nome de joule (J), mesma unidade da grandeza energia.
Importante ressaltar que o trabalho produzido por uma força é nulo (igual a 0) quando esta não provoca deslocamento ou, é perpendicular ao movimento (90º).
Essa nomenclatura é uma homenagem ao físico inglês James Prescott Joule (1818-1889), que contribuiu significativamente para o entendimento da relação entre trabalho mecânico e calor.
Trabalho e Energia
A energia é definida como a capacidade de produzir trabalho, ou seja, um corpo só pode realizar trabalho se possuir energia.
Por exemplo, um guindaste só é capaz levantar um carro (produzir trabalho) quando ligado a uma fonte de energia.
Da mesma forma, só conseguimos fazer nossas atividades normais por recebemos energia dos alimentos que ingerimos.
Talvez se interesse em saber mais sobre energia.
Trabalho de uma Força
Uma força que desloca um corpo produzindo trabalho ao transferir energia para ele, pode ter intensidade, direção e sentido constante ou, alterar-se durante o movimento.
Força constante
Quando uma força constante atua em um corpo, produzindo um deslocamento, o trabalho é calculado usando-se a seguinte fórmula:
T = F . d . cos θ
Sendo,
T: trabalho (J)
F: força (N)
d: deslocamento (m)
θ: ângulo formado entre o vetor força e a direção do deslocamento
Quando o deslocamento acontece no mesmo sentido da componente da força que atua no deslocamento, o trabalho é motor. Ao contrário, quando ocorre em sentido contrário, o trabalho é resistente.
Exemplo:
Uma pessoa quer mudar a posição de um armário e para isso o empurra fazendo uma força constante e paralela ao chão, com intensidade de 50 N, conforme figura abaixo. Sabendo que o deslocamento sofrido pelo armário foi de 3 m, determine o trabalho realizado pela pessoa sobre o armário, nesse deslocamento.
Resolução:
Para encontrar o trabalho da força, podemos substituir diretamente na fórmula os valores informados. Observando que o ângulo θ será igual a zero, pois a direção e o sentido da força e do deslocamento são os mesmos.
Calculando o trabalho:
T = 50 . 3 . cos 0º
T = 150 J
Força variável
Quando a força não é constante, não podemos utilizar a fórmula acima. Contudo, verifica-se que o trabalho é igual, em módulo, a área do gráfico da componente da força pelo deslocamento (F x d).
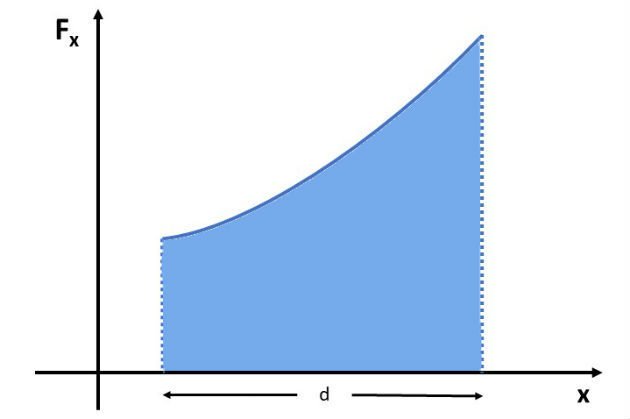
| T |= área da figura
Exemplo:
No gráfico abaixo, representamos a força motora que age no movimento de um carro. Determine o trabalho desta força que atua na direção do movimento do carro, sabendo que o mesmo partiu do repouso.
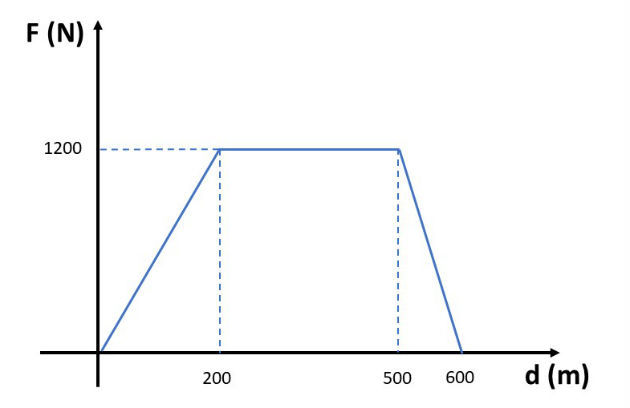
Resolução:
Na situação apresentada, o valor da força não é constante em todo o deslocamento. Sendo assim, vamos calcular o trabalho através do cálculo da área da figura, que nesse caso é um trapézio.
Assim, no deslocamento a força motora fez um trabalho de 540 kJ.
Trabalho da Força Peso
Todos os corpos nas proximidades da superfície da Terra, sofrem a ação de uma força devido ao campo gravitacional terrestre.
Sendo assim, quando um corpo é abandonado de uma determinada altura, ele sofre um deslocamento provocado por esta força, chamada de força peso.
A força peso é calculada por P = m.g. Desta forma, podemos calcular o trabalho da força peso, com sendo:
T = m . g . h
Sendo,
T: trabalho (J)
m: massa do corpo (kg)
g: aceleração da gravidade (m/s2)
h: altura (m)
O trabalho da força peso não depende do caminho, ou seja, seu valor só depende do ponto inicial e final da trajetória.
Quando um corpo está caindo, o trabalho da força peso é motor, ao atuar no mesmo sentido do deslocamento.
Se, ao contrário, o corpo estiver subindo, o trabalho é resistente, pois o peso atua no sentido contrário do deslocamento.
Exemplo:
Um corpo de massa igual a 4 kg é abandonado do alto de um prédio a uma altura de 12 m. Considerando o valor da aceleração da gravidade local igual a 9,8 m/s2, determine o trabalho produzido pela força peso no deslocamento do corpo até o chão.
Solução:
Para calcular o trabalho da força peso, basta multiplicar os valores indicados no enunciado. Como a força peso atua na mesma direção e sentido do deslocamento, o trabalho será positivo.
T = 4 . 9,8 . 12 = 470,4 J
Trabalho da Força Elástica
Quando esticamos ou comprimimos uma mola, verificamos que surge uma força que tenta fazer com que a mola volte a sua posição de equilíbrio.
Essa força, chamada de força elástica, não é constante e sua intensidade varia em função da deformação. Abaixo apresentamos o gráfico da força elástica:
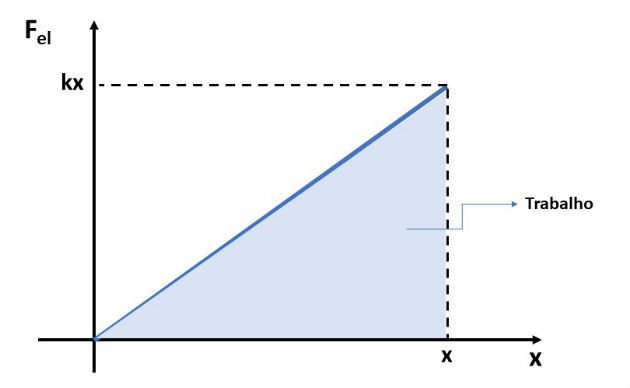
Assim, o módulo do trabalho da força elástica será igual à área da figura, que neste caso é um triângulo. Sendo expresso por:
Onde,
T: trabalho (J)
k: constante elástica da mola (N/m)
x: deformação da mola (m)
O trabalho da força elástica, assim como o trabalho da força peso, também não depende da trajetória. Forças que possuem essa característica são chamadas de conservativas.
Teorema da Energia Cinética
A energia cinética é a energia relacionada com o movimento, ou seja, quando um corpo possui velocidade ele possui energia cinética.
Considerando uma força constante e paralela ao movimento, o trabalho para deslocar um corpo de um ponto A para um ponto B é calculado como:
T = F .d
Nesta fórmula, podemos substituir a força por F = m . a (2ª Lei de Newton) e o deslocamento por d = (vB2 - vA2)/2a (equação de Torricelli). O trabalho pode ser escrito por:
A energia cinética é calculada a partir da seguinte fórmula:
Substituindo na expressão anterior, chegamos ao teorema da energia cinética, ou seja:
T = ECB - ECA = ΔEC
Sendo:
T: trabalho (J)
ΔEC: variação da energia cinética (J)
Desta forma, para um corpo sofrer uma variação de energia cinética é necessário que um trabalho seja feito sobre ele.
Exercícios sobre trabalho na Física
Exercício 1
(Enem - 2015) Uma análise criteriosa do desempenho de Usain Bolt na quebra do recorde mundial dos 100 metros rasos mostrou que, apesar de ser o último dos corredores a reagir ao tiro e iniciar a corrida, seus primeiros 30 metros foram os mais velozes já feitos em um recorde mundial, cruzando essa marca em 3,78 segundos. Até se colocar com o corpo reto, foram 13 passadas, mostrando sua potência durante a aceleração, o momento mais importante da corrida. Ao final deste percurso, Bolt havia atingido a velocidade máxima de 12 m/s.
Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:
a) 5,4×102 J
b) 6,5×103 J
c) 8,6×103 J
d) 1,3×104 J
e) 3,2×104 J
Exercício 2
(UERJ - 2011) Uma pessoa empurrou um carro por uma distância de 26 m, aplicando uma força F de mesma direção e sentido do deslocamento desse carro. O gráfico abaixo representa a variação da intensidade de F, em newtons, em função do deslocamento d, em metros.

Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:
a) 117
b) 130
c) 143
d) 156
Energia Potencial Gravitacional
A energia potencial gravitacional é a energia relacionada com a posição do corpo em relação à superfície terrestre.
Essa energia é igual ao trabalho da força peso ao deslocar o corpo de uma altura h até um ponto de referência. Sendo indicada por:
Epg = T = P . h
Onde:
Epg: energia potencial gravitacional (J)
T: Trabalho (J)
P: força peso (N)
h: altura (m)
Veja também:
Se você está no 1º ano do Ensino Médio, este conteúdo vai te ajudar: Introdução à Física: entenda o que é e todos os principais conceitos
GOUVEIA, Rosimar. Trabalho na Física (produzido por uma força). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/trabalho-na-fisica/. Acesso em:



