Transformação adiabática
As transformações adiabáticas são as mudanças que correm numa massa de gás sem que haja a troca de calor.
O termo adiabático tem origem do grego adiabatos e significa intransponível. O processo adiabático pode ocorrer em duas situações:
- O sistema está isolado e as fronteiras que o cercam impedem que a transferência de calor para o meio externo ocorra.
- O sistema e a vizinhança possuem a mesma temperatura e, por isso, não há diferenças que permitam a transferência de calor.
Para criar um sistema adiabaticamente isolado o recipiente deve ser isolado termicamente.
Transformação adiabática e a Primeira Lei da Termodinâmica
A Primeira Lei da Termodinâmica é também chamada de princípio de conservação de energia, que relaciona a participação do trabalho () e do calor (Q) na variação de energia interna (U) de um sistema.
Como na transformação adiabática não há troca de calor com o ambiente, então Q = 0 e:
Através da fórmula podemos constatar que o módulo da variação de energia do sistema corresponde ao módulo do trabalho realizado entre o sistema e a vizinhança.
Atenção! Um processo adiabático não é o mesmo que transformação isotérmica. Neste último, o prefixo iso indica que a grandeza temperatura é constante.
Na transformação adiabática a temperatura pode variar com a realização de trabalho. O trabalho é responsável pela energia fornecida ou concedida pelo sistema.
Saiba mais sobre a Primeira Lei da Termodinâmica.
Exemplos de transformações adiabáticas
Na prática, as transformações adiabáticas são muito fáceis de acontecer. Veja dois exemplos a seguir.
Expansão de um gás
Na expansão adiabática o gás consegue deslocar o pistão utilizando sua energia interna.
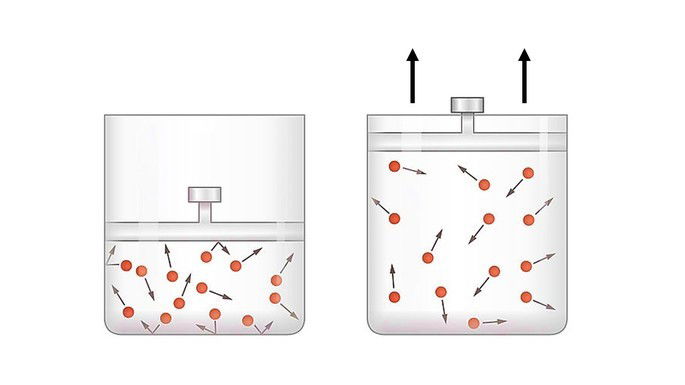
A energia fornecida pelo gás é medida pelo trabalho para que a transformação ocorra. Quando o sistema realiza trabalho, o trabalho é positivo e a variação de energia é negativa
.
Neste caso, a energia interna do sistema diminui proporcionalmente ao trabalho realizado, pois o trabalho é efetuado utilizando a energia interna do sistema.
A expansão adiabática é utilizada no resfriamento de gases, pois a temperatura do sistema diminui e o gás resfria, já que perdeu parte de sua energia interna.
Na prática, podemos observar a expansão de um gás adiabaticamente quando pressionamos um desodorante em spray. Ao tocar no material que se expande da saída percebemos que ele está frio.
Leia também: Estudo dos Gases
Compressão de um gás
Na compressão adiabática o pistão é deslocado por energia proveniente do meio externo.
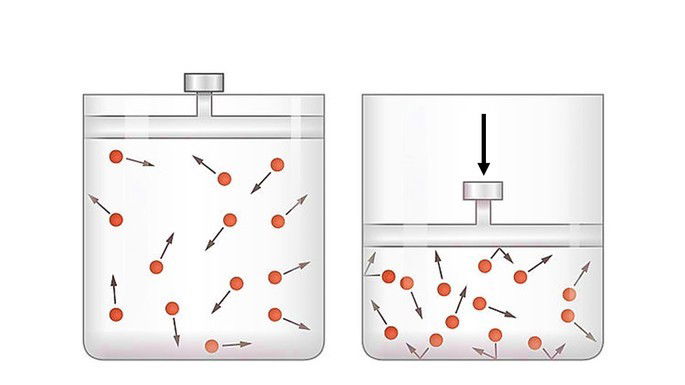
Quando o sistema recebe trabalho, o trabalho é negativo e a variação de energia é positiva
.
Neste caso, a energia interna do sistema aumenta proporcionalmente ao trabalho recebido, pois o sistema está recebendo energia do meio externo.
Observa-se que o sistema aquece pela elevação da temperatura na compressão rápida de um gás.
Na prática, a compressão de um gás adiabaticamente pode ser percebida quando utilizamos uma bomba de ar para encher o pneu de uma bicicleta. Ao tocar no material sentimos que a extremidade da bomba está aquecida.
Leia também: Lei dos Gases
Transformações adiabáticas: variação da pressão e do volume
As grandezas pressão e volume nas transformações adiabáticas são relacionadas pela Equação de Poisson:
Onde,
p: pressão do gás;
V: volume do gás;
y: expoente ou coeficiente de Poisson.
O expoente de Poisson é calculado pela razão entre os calores específicos com pressão (Cp) e volume (Cv) constantes.
O valor do coeficiente depende apenas da atomicidade do gás. Por exemplo, um gás monoatômico, como o hélio (He), tem y igual a 1,7. Já um gás diatômico, como o oxigênio (O2), tem o valor de y igual a 1,4.
Saiba mais sobre as Transformações Gasosas.
Gráfico das transformações adiabáticas
Como o coeficiente de Poisson é maior que 1, o diagrama de pressão e volume em transformações adiabáticas forma hipérboles.
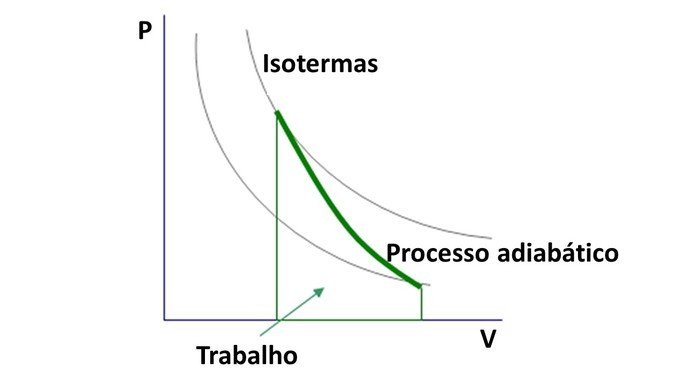
A curva da transformação adiabática intercepta as curvas isotermas, que corresponde ao gráfico de pressão e volume em transformações isotérmicas .
Exercícios sobre transformações adiabáticas
Questão 1
Em uma expansão adiabática, um gás ideal troca a energia de 209 J com o ambiente em forma de trabalho. Determine a quantidade de calor que o sistema troca com o meio externo nesta transformação.
Questão 2
Ao expandir-se adiabaticamente, partindo de uma pressão inicial de 2,0 atm e volume de 2,0 l, um gás dobra seu volume. Determine a pressão final do gás utilizando o coeficiente de Poisson y = 2,0.
a) 1,0 atm
b) 1,5 atm
c) 0,5 atm
d) 2,0 atm
Adquira mais conhecimento lendo também sobre a Transformação isobárica.
Referências Bibliográficas
ÇENGEL,Y. A.; BOLES, M. A. Termodinâmica. 7 ed. Porto Alegre : AMGH, 2013.
HELOU; GUALTER; NEWTON. Tópicos de Física, vol. 2. São Paulo: Editora Saraiva, 2007.
Transformação adiabática. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/transformacao-adiabatica/. Acesso em:

