Variância e desvio padrão

Revisão por Rafael C. Asth

Professor de Matemática e Física

Variância e desvio padrão são medidas de dispersão, ou seja, parâmetros utilizados na Estatística para calcular o quanto os dados de um conjunto de valores podem variar.

A variância (V) permite determinar o afastamento da média que os dados de um conjunto analisado apresentam. Para isso, determina-se o valor médio das diferenças quadradas da média.

O desvio padrão (DP) é calculado a partir da variância, ao ser a raiz quadrada desse parâmetro.

Fórmulas de variância e desvio padrão

Para calcular a variância de todos os valores de um conjunto de dados utiliza-se a fórmula:

$reto sigma ao quadrado espaço igual a espaço numerador começar estilo mostrar soma de reto i espaço igual a espaço 1 para reto n de parêntese esquerdo reto X com reto i subscrito espaço menos espaço reto X em moldura superior parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração$

Onde,

$reto sigma ao quadrado$ : variância
x_i: valor analisado
$reto X em moldura superior$ : média aritmética do conjunto
n: número de dados do conjunto

Essa fórmula representa a variância populacional e para encontrá-la:

Primeiramente, devemos calcular a média aritmética do conjunto;
Em seguida, subtraímos de cada valor do conjunto a média calculada e elevamos o resultado ao quadrado;
Por fim, somamos todos os valores e dividimos pelo número de dados.

Quando o conjunto de dados é muito grande e queremos utilizar uma amostra aleatória devemos empregar a fórmula de variância amostral:

$reto s ao quadrado espaço igual a espaço numerador começar estilo mostrar soma de reto i espaço igual a espaço 1 para reto n de parêntese esquerdo reto X com reto i subscrito espaço menos espaço reto X em moldura superior parêntese direito ao quadrado fim do estilo sobre denominador reto n espaço menos espaço 1 fim da fração$

Como o desvio padrão é expresso pela raiz quadrada da variância, basta que seja extraída a raiz do resultado calculado pela fórmula anterior.

$DP espaço igual a espaço raiz quadrada de reto sigma ao quadrado fim da raiz espaço ou espaço DP espaço estreito igual a espaço estreito raiz quadrada de reto s ao quadrado fim da raiz$

Portanto, o desvio padrão é um dado que apresenta a mesma unidade do conjunto de números na amostra, o que é útil para a análise e comparação.

Saiba mais sobre as medidas de dispersão.

Como calcular a variância e o desvio padrão

Utilizaremos como exemplo a figura abaixo, que apresenta a altura de quatro construções (em metros), para calcular o desvio padrão e a variância.

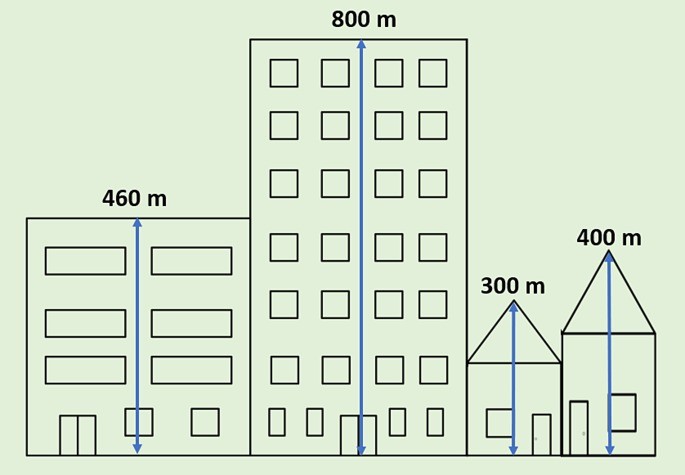
1º passo: calcular a média aritmética dos valores.

Para calcular a média deve-se somar todas as alturas e dividir pelo número de dados apresentados.

$reto X em moldura superior espaço igual a espaço numerador reto x com 1 subscrito espaço mais espaço reto x com 2 subscrito espaço mais espaço reto x com 3 subscrito espaço mais espaço reto x com 4 subscrito sobre denominador 4 fim da fração espaço reto X em moldura superior espaço igual a espaço numerador 460 espaço reto m espaço mais espaço 800 espaço reto m espaço mais espaço 300 espaço reto m espaço mais espaço 400 espaço reto m sobre denominador 4 fim da fração reto X em moldura superior espaço igual a espaço numerador 1960 espaço reto m sobre denominador 4 fim da fração reto X em moldura superior espaço igual a espaço 490 espaço reto m$

Observe na imagem a seguir o quanto cada altura se distancia da média.

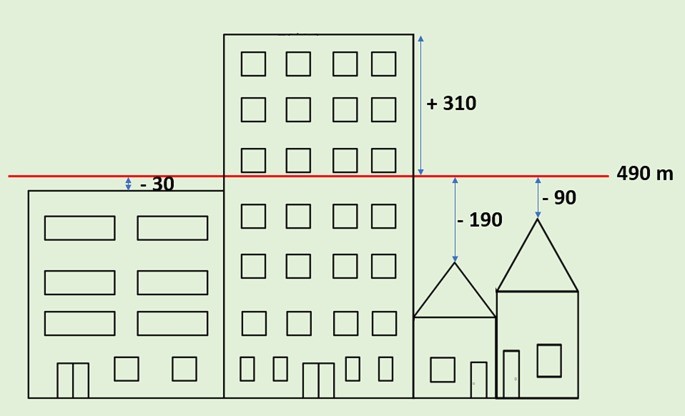
2º passo: calcular a variância

Agora, substituímos a média ( $reto X em moldura superior$ ) e os valores do conjunto (X_n) na fórmula de variância.

$reto sigma ao quadrado igual a espaço numerador parêntese esquerdo reto x com 1 subscrito espaço – espaço reto M com reto A subscrito parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 2 subscrito espaço – espaço reto M com reto A subscrito parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 3 subscrito espaço – espaço reto M com reto A subscrito parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 4 subscrito espaço – espaço reto M com reto A subscrito parêntese direito ao quadrado espaço sobre denominador 4 fim da fração reto sigma ao quadrado espaço igual a espaço numerador parêntese esquerdo 460 espaço – espaço 490 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 800 espaço – espaço 490 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 300 espaço – espaço 490 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 400 espaço – espaço 490 parêntese direito ao quadrado sobre denominador 4 fim da fração espaço reto sigma ao quadrado espaço igual a espaço numerador parêntese esquerdo menos 30 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 310 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 190 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 90 parêntese direito ao quadrado sobre denominador 4 fim da fração espaço reto sigma ao quadrado espaço igual a espaço numerador 900 espaço reto m ao quadrado espaço mais espaço 96100 espaço reto m ao quadrado espaço mais espaço 36100 espaço reto m ao quadrado espaço mais espaço 8100 espaço reto m ao quadrado sobre denominador 4 fim da fração reto sigma ao quadrado espaço igual a espaço numerador 141200 espaço reto m ao quadrado sobre denominador 4 fim da fração reto sigma ao quadrado espaço igual a espaço 35300 espaço reto m ao quadrado$

3º passo: calcular o desvio padrão

Para encontrar o desvio padrão basta tirar a raiz quadrada do valor da variância.

$DP espaço igual a espaço raiz quadrada de reto sigma ao quadrado fim da raiz DP espaço estreito igual a espaço estreito raiz quadrada de 35300 espaço reto m ao quadrado fim da raiz DP espaço aproximadamente igual espaço 188 espaço reto m$

Observe a imagem a seguir com a sinalização do desvio padrão. Podemos perceber que dois prédios estão próximos de um “padrão” enquanto dois estão acima e abaixo, respectivamente.

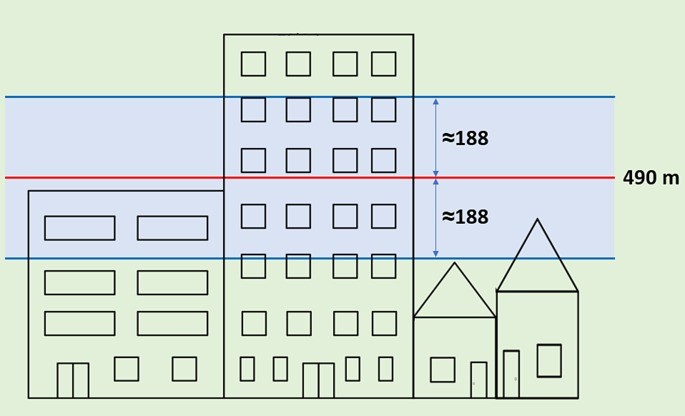
Saiba mais sobre desvio padrão.

Exercícios resolvidos sobre variância e desvio padrão

Questão 1

Calcule o desvio padrão dos seguintes conjuntos de valores:

a) 148 – 170 – 155 – 131

Ver Resposta

Resposta correta: V = 196,5 e DP ≈ 14.

1º passo: calcular a média aritmética.

$reto X em moldura superior espaço estreito igual a espaço numerador 148 espaço mais espaço 170 espaço mais espaço 155 espaço mais espaço 131 sobre denominador 4 fim da fração reto X em moldura superior espaço igual a espaço 604 sobre 4 igual a espaço 151$

2º passo: calcular a variância

$reto sigma ao quadrado igual a numerador parêntese esquerdo reto x com 1 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 2 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 3 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 4 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço sobre denominador 4 fim da fração reto sigma ao quadrado igual a numerador parêntese esquerdo 148 espaço – espaço 151 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 170 espaço – espaço 151 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 155 espaço – espaço 151 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 131 espaço – espaço 151 parêntese direito ao quadrado sobre denominador 4 fim da fração espaço reto sigma ao quadrado igual a numerador parêntese esquerdo 3 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 19 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 20 parêntese direito ao quadrado sobre denominador 4 fim da fração espaço reto sigma ao quadrado igual a numerador 9 espaço mais espaço 361 espaço mais espaço 16 espaço mais espaço 400 sobre denominador 4 fim da fração reto sigma ao quadrado igual a 786 sobre 4 espaço igual a espaço 196 vírgula 5$

3º passo: calcular o desvio padrão

$DP espaço igual a espaço raiz quadrada de reto sigma ao quadrado fim da raiz DP espaço igual a espaço raiz quadrada de 196 vírgula 5 fim da raiz DP espaço aproximadamente igual espaço 14$

b) 86 – 92 – 91 – 95 – 90 – 89 – 94

Ver Resposta

Resposta correta: V = 8 e DP ≈ 2,83.

1º passo: calcular a média aritmética.

$reto X em moldura superior espaço estreito igual a espaço numerador 86 espaço mais espaço 92 espaço mais espaço 91 espaço mais espaço 95 espaço mais espaço 90 espaço mais espaço 89 espaço mais espaço 94 sobre denominador 7 fim da fração reto X em moldura superior espaço igual a espaço 637 sobre 7 igual a espaço 91$

2º passo: calcular a variância

$reto sigma ao quadrado igual a numerador parêntese esquerdo reto x com 1 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 2 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 3 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço mais espaço parêntese esquerdo reto x com 4 subscrito espaço – espaço reto X em moldura superior parêntese direito ao quadrado espaço sobre denominador 7 fim da fração reto sigma ao quadrado igual a numerador parêntese esquerdo 86 – 91 parêntese direito ao quadrado mais parêntese esquerdo 92 – 91 parêntese direito ao quadrado mais parêntese esquerdo 91 – 91 parêntese direito ao quadrado mais parêntese esquerdo 95 – 91 parêntese direito ao quadrado mais parêntese esquerdo 90 – 91 parêntese direito ao quadrado mais parêntese esquerdo 89 – 91 parêntese direito ao quadrado mais parêntese esquerdo 94 – 91 parêntese direito ao quadrado sobre denominador 4 fim da fração espaço reto sigma ao quadrado igual a numerador parêntese esquerdo menos 5 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 1 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 0 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 1 parêntese direito ao quadrado mais espaço parêntese esquerdo menos 2 parêntese direito ao quadrado mais espaço parêntese esquerdo 3 parêntese direito ao quadrado sobre denominador 7 fim da fração espaço reto sigma ao quadrado igual a numerador 25 espaço mais espaço 1 espaço mais espaço 0 espaço mais espaço 16 espaço mais espaço 1 espaço mais espaço 4 espaço mais espaço 9 sobre denominador 7 fim da fração reto sigma ao quadrado igual a 56 sobre 7 espaço igual a espaço 8$

3º passo: calcular o desvio padrão

$DP espaço igual a espaço raiz quadrada de reto sigma ao quadrado fim da raiz DP espaço igual a espaço raiz quadrada de 8 DP espaço aproximadamente igual espaço 2 vírgula 83$

Questão 2

A eleição para conselheiro tutelar de uma cidade contava com dois candidatos. Observe na tabela a seguir a quantidade de votos válidos recebidos por cada um deles nas 5 urnas utilizadas para depositar os votos.

Candidato	Urna 1	Urna 2	Urna 3	Urna 4	Urna 5
A	17	18	21	13	20
B	22	12	19	23	11

Qual candidato obteve a melhor média de votos e o menor desvio padrão nas 5 urnas?

a) Candidato A
b) Candidato B
c) Os dois candidatos

Ver Resposta

Alternativa correta: a) Candidato A.

Candidato A:

Média aritmética:

$reto X em moldura superior espaço igual a espaço numerador 17 espaço mais espaço 18 espaço mais espaço 21 espaço mais espaço 13 espaço mais espaço 20 sobre denominador 5 fim da fração espaço espaço igual a espaço 89 sobre 5 espaço igual a espaço 17 vírgula 8$

Variância:

$reto sigma ao quadrado igual a numerador parêntese esquerdo 17 – 17 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 18 – 17 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 21 – 17 vírgula 8 parêntese direito à potência de 2 espaço fim do exponencial mais espaço parêntese esquerdo 13 – 17 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 20 – 17 vírgula 8 parêntese direito ao quadrado espaço sobre denominador 5 fim da fração reto sigma ao quadrado igual a numerador parêntese esquerdo menos 0 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 0 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 3 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 4 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 2 vírgula 2 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a numerador 0 vírgula 64 espaço mais espaço 0 vírgula 04 espaço mais espaço 10 vírgula 24 espaço mais espaço 23 vírgula 04 espaço mais espaço 4 vírgula 84 sobre denominador 5 fim da fração reto sigma ao quadrado igual a numerador 38 vírgula 8 sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a 7 vírgula 76$

Desvio padrão

$D P espaço igual a espaço estreito raiz quadrada de 7 vírgula 76 fim da raiz D P espaço igual a espaço 2 vírgula 79$

Candidato B:

Média aritmética:

$reto X em moldura superior espaço igual a espaço numerador 22 espaço mais espaço 12 espaço mais espaço 19 espaço mais espaço 23 espaço mais espaço 11 sobre denominador 5 fim da fração espaço espaço igual a espaço 87 sobre 5 espaço igual a espaço 17 vírgula 4$

Variância:

$reto sigma ao quadrado espaço igual a espaço numerador parêntese esquerdo 22 – 17 vírgula 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 12 – 17 vírgula 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 19 – 17 vírgula 4 parêntese direito à potência de 2 espaço fim do exponencial mais espaço parêntese esquerdo 23 – 17 vírgula 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 11 – 17 vírgula 4 parêntese direito ao quadrado espaço sobre denominador 5 fim da fração reto sigma ao quadrado espaço igual a espaço numerador parêntese esquerdo 4 vírgula 6 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 5 vírgula 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 1 vírgula 6 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 5 vírgula 6 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 6 vírgula 4 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado espaço igual a espaço numerador 21 vírgula 16 espaço mais espaço 29 vírgula 16 espaço mais espaço 2 vírgula 56 espaço mais espaço 31 vírgula 36 espaço mais espaço 40 vírgula 96 sobre denominador 5 fim da fração reto sigma ao quadrado espaço igual a espaço numerador 125 vírgula 2 sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado espaço igual a espaço 25 vírgula 04$

Desvio padrão:

$D P espaço igual a espaço raiz quadrada de 25 vírgula 04 fim da raiz D P espaço aproximadamente igual 5 espaço$

Questão 3

Três alunos estavam treinando para uma corrida que aconteceria nos jogos escolares e o treinador anotava a distância alcançada por cada um deles ao realizar 5 voltas individualmente em um tempo fixo. Confira o resultado na tabela a seguir.

Aluno	Volta 1	Volta 2	Volta 3	Volta 4	Volta 5
João	210 m	198 m	215 m	210 m	196 m
Carlos	189 m	190 m	203 m	197 m	192 m
Pedro	204 m	201 m	199 m	188 m	193 m

Qual dos alunos obteve o resultado mais regular?

a) João
b) Carlos
c) Pedro
d) Os três tiveram o mesmo resultado.

Ver Resposta

Alternativa correta: b) Carlos, pois apresentou o menor desvio padrão.

1º passo: calcular a média aritmética de cada atleta.

Para isso, somamos as distâncias percorridas e dividimos pelo número de voltas.

$reto X em moldura superior com parêntese esquerdo João parêntese direito subscrito fim do subscrito dois pontos espaço numerador 210 espaço mais espaço 198 espaço mais espaço 215 espaço mais espaço 210 espaço mais espaço 196 sobre denominador 5 fim da fração espaço igual a espaço 1029 sobre 5 espaço igual a espaço 205 vírgula 8 espaço reto m espaço espaço reto X em moldura superior com parêntese esquerdo Carlos parêntese direito subscrito fim do subscrito dois pontos espaço numerador 189 espaço mais espaço 190 espaço mais espaço 203 espaço mais espaço 197 espaço mais espaço 192 sobre denominador 5 fim da fração igual a espaço 971 sobre 5 igual a espaço 194 vírgula 2 espaço reto m espaço espaço reto X em moldura superior com parêntese esquerdo Pedro parêntese direito subscrito fim do subscrito dois pontos espaço numerador 204 espaço mais espaço 201 espaço mais espaço 199 espaço mais espaço 188 espaço mais espaço 193 sobre denominador 5 fim da fração igual a 985 sobre 5 espaço igual a espaço 197 espaço reto m$

2º passo: Calcular a variância do desempenho de cada atleta.

João

$reto sigma ao quadrado igual a numerador parêntese esquerdo 210 – 205 vírgula 8 parêntese direito ao quadrado mais parêntese esquerdo 198 – 205 vírgula 8 parêntese direito ao quadrado mais parêntese esquerdo 215 – 205 vírgula 8 parêntese direito ao quadrado mais parêntese esquerdo 210 – 205 vírgula 8 parêntese direito ao quadrado mais parêntese esquerdo 196 – 205 vírgula 8 parêntese direito ao quadrado sobre denominador 5 fim da fração reto sigma ao quadrado igual a numerador parêntese esquerdo 4 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 7 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 9 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 4 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 9 vírgula 8 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço reto sigma ao quadrado igual a numerador 17 vírgula 64 espaço reto m ao quadrado espaço mais espaço 60 vírgula 84 espaço reto m ao quadrado espaço mais espaço 84 vírgula 64 espaço reto m ao quadrado espaço mais espaço 17 vírgula 64 espaço reto m ao quadrado espaço mais espaço 96 vírgula 04 espaço reto m sobre denominador 5 fim da fração ao quadrado reto sigma ao quadrado igual a numerador 276 vírgula 8 espaço reto m ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a 55 vírgula 36 espaço reto m ao quadrado$

Carlos

$reto sigma ao quadrado igual a numerador parêntese esquerdo 189 menos 194 vírgula 2 parêntese direito ao quadrado mais parêntese esquerdo 190 menos 194 vírgula 2 parêntese direito ao quadrado mais parêntese esquerdo 203 menos 194 vírgula 2 parêntese direito ao quadrado mais parêntese esquerdo 197 menos 194 vírgula 2 parêntese direito ao quadrado mais parêntese esquerdo 192 menos 194 vírgula 2 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço reto sigma ao quadrado igual a numerador parêntese esquerdo menos 5 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 4 vírgula 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 8 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 2 vírgula 8 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 2 vírgula 2 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço reto sigma ao quadrado igual a numerador 27 vírgula 04 espaço reto m ao quadrado espaço mais espaço 17 vírgula 64 espaço reto m ao quadrado espaço mais espaço 77 vírgula 44 espaço reto m ao quadrado espaço mais espaço 7 vírgula 84 espaço reto m ao quadrado espaço mais espaço 4 vírgula 84 espaço reto m ao quadrado sobre denominador 5 fim da fração espaço reto sigma ao quadrado igual a numerador 134 vírgula 8 espaço reto m ao quadrado sobre denominador 5 fim da fração reto sigma ao quadrado igual a 26 vírgula 96 espaço reto m ao quadrado$

Pedro

$reto sigma ao quadrado igual a numerador parêntese esquerdo 204 menos 197 parêntese direito ao quadrado mais parêntese esquerdo 201 menos 197 parêntese direito ao quadrado mais parêntese esquerdo 199 menos 197 parêntese direito ao quadrado mais parêntese esquerdo 188 menos 197 parêntese direito ao quadrado mais parêntese esquerdo 193 menos 197 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a numerador parêntese esquerdo 7 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 4 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo 2 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 9 parêntese direito ao quadrado espaço mais espaço parêntese esquerdo menos 4 parêntese direito ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a numerador 49 espaço reto m ao quadrado espaço mais espaço 16 espaço reto m ao quadrado espaço mais espaço 4 espaço reto m à potência de 2 espaço fim do exponencial mais espaço 81 espaço reto m ao quadrado espaço mais espaço 16 espaço reto m ao quadrado sobre denominador 5 fim da fração espaço espaço reto sigma ao quadrado igual a numerador 166 espaço reto m ao quadrado sobre denominador 5 fim da fração espaço reto sigma ao quadrado igual a 33 vírgula 2 espaço reto m ao quadrado$

3º passo: Calcular o desvio padrão

João

$DP espaço estreito igual a espaço estreito raiz quadrada de 55 vírgula 36 espaço reto m ao quadrado fim da raiz espaço DP espaço estreito igual a espaço estreito 7 vírgula 44 espaço reto m$

Carlos

$DP espaço estreito igual a espaço estreito raiz quadrada de 26 vírgula 96 espaço reto m ao quadrado fim da raiz espaço DP espaço estreito igual a espaço estreito 5 vírgula 19 espaço reto m$

Pedro

$DP espaço estreito igual a espaço estreito raiz quadrada de 33 vírgula 2 espaço reto m ao quadrado fim da raiz espaço DP espaço estreito igual a espaço 5 vírgula 76 espaço reto m$

Questão 4

Durante o ano de 2020 foi realizado pelo Procon um levantamento de preços de dois itens da cesta básica nos 5 supermercados existentes uma pequena cidade. O resultado está apresentado na tabela abaixo (em R$) para alimentos da mesma marca.

Arroz (1 kg)	6,90	8,90	7,78	8,83	6,48	9,04
Feijão (1 kg)	8,20	7,90	9,05	8,40	7,59	10,99

a) Qual é a média, a variância e o desvio padrão dos preços de cada alimento?

Ver Resposta

Respostas corretas:

Arroz: M = 7,99; V = 1,025; DP = 1,012
Feijão: M = 8,69; V = 1,26; DP = 1,12

Arroz

Média aritmética:

$reto M espaço igual a espaço numerador 6 vírgula 90 mais 8 vírgula 90 mais 7 vírgula 78 mais 8 vírgula 83 mais 6 vírgula 48 mais 9 vírgula 04 sobre denominador 6 fim da fração espaço igual a espaço numerador 47 vírgula 93 sobre denominador 6 fim da fração espaço igual a espaço 7 vírgula 99 espaço$

Variância

V = (6,90 - 7,99)² + (8,90 - 7,99)² + (7,78 - 7,99)² + (8,83 - 7,99)² + (6,48 - 7,99)² + (9,04 - 7,99)² / 6

V = (-1,09)² + (0,91)² + (-0,21)² + (0,84)² + (-1,51)² + (1,05)² / 6

V = 1,1881 + 0,8281 + 0,0441 + 0,7056 + 2,2801 + 1,1025/ 6

V = 6,1485 / 6

V = 1,025

Desvio padrão

$DP espaço estreito igual a espaço estreito raiz quadrada de 1 vírgula 025 fim da raiz espaço DP espaço estreito igual a espaço estreito 1 vírgula 012$

Feijão

Média aritmética

$reto M espaço igual a espaço numerador 8 vírgula 20 mais 7 vírgula 90 mais 9 vírgula 05 mais 8 vírgula 40 mais 7 vírgula 59 mais 10 vírgula 99 sobre denominador 6 fim da fração espaço igual a espaço numerador 52 vírgula 13 sobre denominador 6 fim da fração espaço igual a espaço 8 vírgula 69 espaço$

Variância

V = (8,20 - 8,69)² + (7,90 - 8,69)² + (9,05 - 8,69)² + (8,40 - 8,69)² + (7,59 - 8,69)² + (10,99 - 8,69)² / 6

V = (-0,49)² + (0,79)² + (0,36)² + (-0,29)² + (-1,1)² + (2,3)² / 6

V = 0,2401 + 0,6241 + 0,1296 + 0,0841 + 1,21 + 5,29 / 6

V = 7,5779 / 6

V = 1,26

Desvio padrão

$DP espaço estreito igual a espaço estreito raiz quadrada de 1 vírgula 26 fim da raiz espaço DP espaço estreito igual a espaço estreito 1 vírgula 12$

b) Qual alimento apresenta os preços mais homogêneos?

Ver Resposta

Resposta correta: O arroz, pois tem o menor desvio padrão.

Pratique mais com:

Complemente seus estudos com os conteúdos:

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações