Velocidade relativa: o que é, como calcular, exemplos
A velocidade relativa é o conceito que analisa as velocidades de diferentes corpos em movimento, descrevendo a velocidade de um objeto em relação a outro que também está em movimento.
Nesse contexto, o referencial passa a ser o movimento de um dos corpos, e tanto a direção quanto o sentido dos movimentos devem ser considerados, já que a velocidade relativa é uma grandeza vetorial.
O estudo da velocidade relativa responde questões como: em que momento dois objetos em movimento irão se encontrar, qual será a posição de um em relação ao outro após um intervalo de tempo, ou como comparar suas velocidades.
Esse conceito é essencial para entender situações práticas de movimento, como carros em uma rodovia, aviões em voo ou barcos navegando em rios com correnteza.
As mesmas equações utilizadas no Movimento Uniforme (MU) e do Movimento Uniformemente Variado (MUV) podem ser aplicadas para calcular a velocidade relativa.
Como Determinar a Velocidade Relativa
A velocidade relativa depende dos vetores de velocidade dos dois corpos. Existem duas situações principais:
Velocidade relativa com mesma direção e sentido
Para determinar a velocidade relativa de móveis com mesma direção e sentido (como carros em uma ultrapassagem), os módulos das velocidades são subtraídos.
Onde:
- Vrel é a velocidade relativa;
- V1 e V2 são as velocidades de cada móvel.
Esta fórmula é válida tanto em situações de aproximação quanto de afastamento entre os móveis.
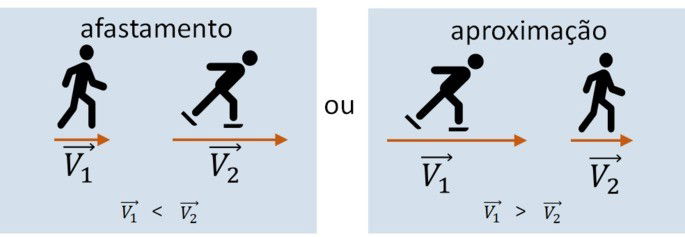
Exemplo de cálculo de velocidade relativa com mesma direção e sentido:
Um caminhão trafega com uma velocidade constante de 80 km/h em uma rodovia de duas pistas no mesmo sentido. Um motociclista, localizado 100 metros atrás do para-brisa do caminhão, deseja ultrapassá-lo.
Considerando que tanto o caminhão quanto a moto mantêm velocidades constantes e desconsiderando as dimensões da moto, responda às perguntas a seguir:
a) Qual a velocidade relativa entre a moto e caminhão?
Como o movimento é de mesma direção e sentido, devemos subtrair os módulos das velocidades.
Isto equivale a dizer que a moto se afasta do caminhão como se estivesse andando a 20 km/h enquanto o caminhão se mantém parado.
Por isso, em uma ultrapassagem, mesmo em alta velocidade em relação à estrada, nos movemos lentamente em relação ao outro veículo, pois a velocidade relativa entre os dois é menor que o módulo da velocidade em relação à estrada.
b) Em quanto tempo a moto completará a ultrapassagem, considerando o instante descrito no enunciado como a origem do movimento?
Dados:
- Movimento com mesma direção e sentido.
- Vmoto = 100 km/h
- Vcaminhão = 80 km/h
- Distância entre os veículos = 100 m = 0,1 km
As funções horárias das posições dos dois móveis são:
Smoto = S0 + Vt
Smoto = 0 + 100t
Smoto = 100t
Scaminhão = S0 +Vt
Scaminhão = 0,1 + 80t
No instante da ultrapassagem as posições serão iguais.
Smoto = Scaminhão
100t = 0,1 + 80t
100t - 80t = 0,1
20t = 0,1
t=0,1/20 = 0,005 h
Passando para minutos
0,005 x 60 = 0,3 min
Passando para segundos
0,3 x 60 = 18 s
Portanto, levará 18 s para a moto completar a ultrapassagem.
c) A partir do momento que a moto completa a ultrapassagem, após 1 min, ela estará a que distância do caminhão?
Considerando o momento da ultrapassagem como origem das posições e do tempo, e tendo que as velocidades continuam constantes, as funções horárias são:
- Smoto = 100t
- Scaminhão = 80t
1 min equivale a 1/60 h.
Substituindo nas funções horárias:
Para a moto:
Para o caminhão:
Fazendo a subtração das distâncias que cada veículo percorreu 1 min após a ultrapassagem:
Smoto - Scaminhão = 1,666 - 1,333 = 0,333 km ou 333 m.
Velocidade relativa com mesma direção e sentidos opostos
Para determinar a velocidade relativa entre móveis com mesma direção e sentidos opostos, somam-se os módulos das velocidades.
Onde:
- Vrel é a velocidade relativa;
- V1 e V2 são as velocidades de cada móvel.
Esta fórmula é válida tanto em situações de aproximação quanto de afastamento entre os móveis.
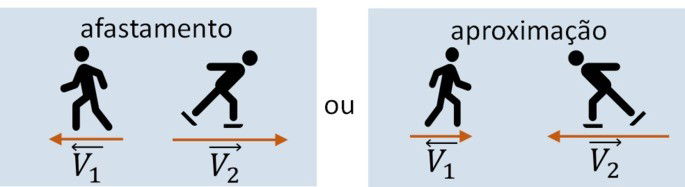
Exemplo de cálculo de velocidade relativa com mesma direção e sentidos opostos:
Dois trens partiram das cidades A e B, cada um tendo como destino a cidade de onde o outro saiu. Estas cidades estão distantes 440 km uma da outra. O trem que parte da cidade A anda a uma velocidade de 50 km/h, enquanto o que partiu da cidade B, 60 km/h. Suas linhas férreas mantêm-se paralelas ao longo do percurso.
a) Qual a velocidade relativa entre os trens?
Como estão em sentidos opostos, somamos as velocidades.
b) Em quanto tempo se encontrarão?
As funções horárias das posições, adotando como sentido positivo a direção de A para B:
Para o trem que partiu de A:
Para o trem que partiu de B:
Estes se encontrarão quando , desta forma:
Portanto, eles demorarão 4 h para se encontrarem.
c) Um trem partindo da cidade A e indo para a cidade B, mantendo uma velocidade constante de 110 km/h levaria quanto tempo para completar a viagem de 440 km?
O mesmo tempo, 4h, pois
Isto equivale a dizer que os trens se aproximarão um do outro como se um estivesse parado e o outro a uma velocidade de 110 km/h.
Exercícios sobre velocidade relativa
Questão 1
(CESGRANRIO-RJ) Um trem sai da estação de uma cidade, em percurso retilíneo, com velocidade constante de 50 km/h. Quanto tempo depois de sua partida deverá sair, da mesma estação, um segundo trem com velocidade constante de 75 km/h para alcançá-lo a 120 km da cidade?
a) 24 min
b) 48 min
c) 96 min
d) 144 min
e) 288 min
Questão 2
(UFMG 2009) Numa corrida, Rubens Barrichelo segue atrás de Felipe Massa, em um trecho da pista reto e plano. Inicialmente, os dois carros movem-se com velocidades constantes, de mesmos módulos, direção e sentido. No instante t1, Felipe aumenta a velocidade de seu carro com aceleração constante; e, no instante t2, Barrichelo também aumenta a velocidade do seu carro com a mesma aceleração.
Considerando essas informações, assinale a alternativa cujo gráfico melhor descreve o módulo da velocidade relativa entre os dois veículos, em função do tempo.
a) 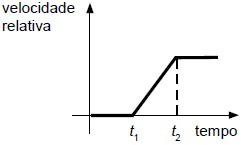
b) 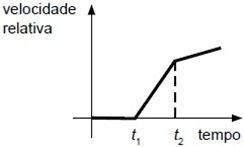
c)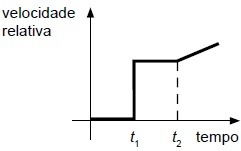
d)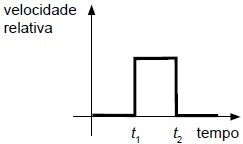
Você pode se interessar por:
- Movimento Uniforme
- Movimento Uniformemente Variado
- Velocidade Média
- Equação de Torricelli
- Cinemática
- Exercícios sobre velocidade média
ASTH, Rafael. Velocidade relativa: o que é, como calcular, exemplos. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/velocidade-relativa/. Acesso em:


