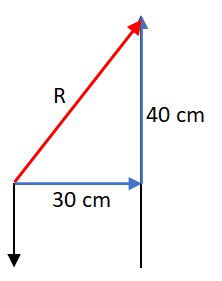
Vetores: soma, subtração e decomposição

Rafael C. Asth

Professor de Matemática e Física

Vetores são setas que têm como características a direção, o módulo e o sentido. Na Física, além dessas características, os vetores têm nomes. Isso porque eles representam grandezas (força, aceleração, por exemplo). Se estivermos falando sobre o vetor aceleração, uma seta (vetor) estará em cima da letra a.

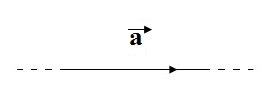Direção horizontal, módulo e sentido (da esquerda para a direita) do vetor aceleração

Soma de Vetores

A adição de vetores pode ser feita através de duas regras, seguindo os seguintes passos:

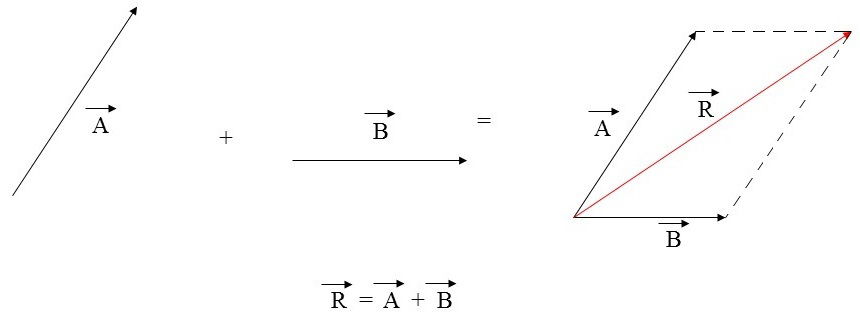
Regra do Paralelogramo

1.º Junte as origens dos vetores.
2.º Trace uma linha paralela a cada um dos vetores, formando um paralelogramo.
3.º Some a diagonal do paralelogramo.

Importa referir que nesta regra podemos somar apenas 2 vetores de cada vez. Para somar três ou mais vetores, fazemos a soma de e, a resultante, somamos ao terceiro vetor , e assim por diante.

Módulo do Vetor Soma

O valor, módulo ou intensidade do vetor soma é o número obtido utilizando a lei dos cossenos.

Sendo r, a e b os módulos dos vetores, , e , r é dado por:

Onde é o ângulo formado entre os vetores e .

Regra da Poligonal

1.º Junte os vetores, um pela origem, outro pela extremidade (ponta). Faça assim sucessivamente, conforme o número de vetores que precisa somar.
2.º Trace uma linha perpendicular entre a origem do 1.º vetor e a extremidade do último vetor.
3.º Some a linha perpendicular.

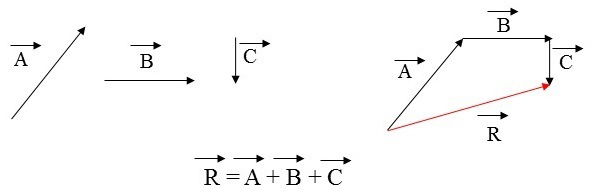
Importa referir que nesta regra podemos somar vários vetores por vez.

Vale a propriedade comutativa da adição, por isso, a ordem em que se somam os vetores, não altera o resultado.

Caso a linha poligonal formada pelos vetores for fechada, o vetor resultante será nulo.

Subtração de Vetores

A operação de subtração de vetores pode ser feita pelas mesmas regras da adição.

Regra do Paralelogramo

1.º Faça linhas paralelas a cada um dos vetores, formando um paralelogramo.
2.º De seguida, faça o vetor resultante, o vetor que liga a extremidade do segundo para o primeiro vetor.
3.º Faça a subtração, considerando que -B é o vetor oposto de B.

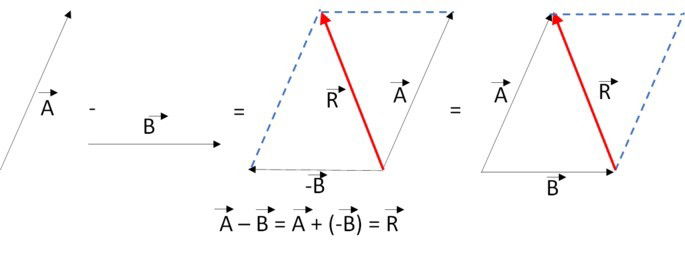
Ao posicionar os dois vetores, com mesma origem e conservando as direções e sentidos, o vetor resultante é o vetor que liga o final do segundo vetor na subtração (subtraendo), até o final do primeiro (minuendo).

Módulo do Vetor Subtração

O valor, módulo ou intensidade do vetor subtração é o número obtido utilizando a lei dos cossenos.

Sendo r, a e b os módulos dos vetores , e , r é dado por

Onde é o ângulo formado entre os vetores e .

Regra da Poligonal

1.º Junte os vetores, um pela origem, outro pela extremidade (ponta). Faça assim sucessivamente, conforme o número de vetores que precisa somar.
2.º Faça uma linha perpendicular entre a origem do 1.º vetor e a extremidade do último vetor.
3.º Faça a subtração da linha perpendicular, considerando que -B é o vetor oposto de B.

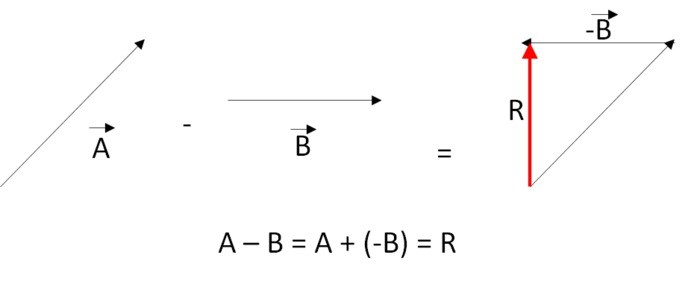
Decomposição de Vetores

Na decomposição vetorial, através de um único vetor podemos encontrar as componentes em dois eixos. Esses componentes são a soma de dois vetores que resultam no vetor inicial.

A regra do paralelogramo também pode ser usada nessa operação:

1.º Trace dois eixos perpendiculares entre si com origem no vetor existente.
2.º Trace uma linha paralela a cada um dos vetores, formando um paralelogramo.
3.º Some as componentes e e verifique que o seu resultado é igual ao do vetor que havia inicialmente.

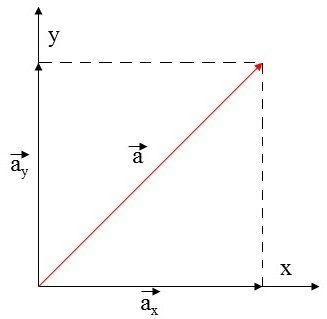
Neste caso, o módulo do vetor é obtido pelo teorema de Pitágoras.

Saiba mais:

• Vetores
• Força
• Aceleração
• Grandezas Vetoriais

Exercícios

Exercício 1

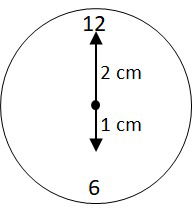
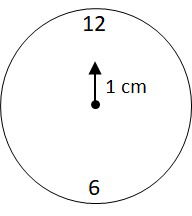
(PUC-RJ) Os ponteiros de hora e minuto de um relógio suíço têm, respectivamente, 1 cm e 2 cm. Supondo que cada ponteiro do relógio é um vetor que sai do centro do relógio e aponta na direção dos números na extremidade do relógio, determine o vetor resultante da soma dos dois vetores correspondentes aos ponteiros de hora e minuto quando o relógio marca 6 horas.

a) O vetor tem módulo 1 cm e aponta na direção do número 12 do relógio.
b) O vetor tem módulo 2 cm e aponta na direção do número 12 do relógio.
c) O vetor tem módulo 1 cm e aponta na direção do número 6 do relógio.
d) O vetor tem módulo 2 cm e aponta na direção do número 6 do relógio.
e) O vetor tem módulo 1,5 cm e aponta na direção do número 6 do relógio.

Exercício 2

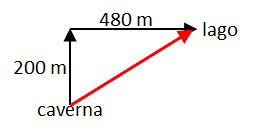
(UFAL-AL) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago era, em metros,

a) 680
b) 600
c) 540
d) 520
e) 500

Exercício 3

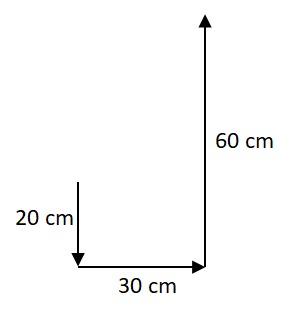
(UDESC) Um "calouro" do Curso de Física recebeu como tarefa medir o deslocamento de uma formiga que se movimenta em uma parede plana e vertical. A formiga realiza três deslocamentos sucessivos:

1) um deslocamento de 20 cm na direção vertical, parede abaixo;
2) um deslocamento de 30 cm na direção horizontal, para a direita;
3) um deslocamento de 60 cm na direção vertical, parede acima.

No final dos três deslocamentos, podemos afirmar que o deslocamento resultante da formiga tem módulo igual a:

a) 110 cm
b) 50 cm
c) 160 cm
d) 10 cm

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.