Cálculo da Área do Cone: fórmulas e exercícios

Revisão por Rafael C. Asth

Professor de Matemática e Física

A área do cone faz referência a medida da superfície dessa figura geométrica espacial. Lembre-se que o cone é um sólido geométrico com uma base circular e uma ponta, a qual é chamada de vértice.

Cone

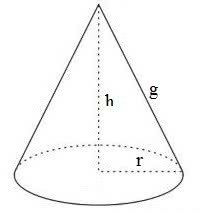
No cone é possível calcular três áreas:

Fórmula da área da base

A_b = π.r²

Onde:

A_b: área da base
π (pi): 3,14
r: raio

Fórmula da área Lateral

A_l= π.r.g

Onde:

A_l: área lateral
π (pi): 3,14
r: raio
g: geratriz

Obs: A geratriz corresponde a medida da lateral do cone. Formada por qualquer segmento que tenha uma extremidade no vértice e a outra na base ela é calculada pela fórmula: g² = h² + r²(sendo h a altura do cone e r o raio)

Fórmula da área total

At = π.r (g+r)

Onde:

A_t: área total
π (pi): 3,14
r: raio
g: geratriz

Área do Tronco do Cone

O chamado “tronco do cone” corresponde a parte que contém a base dessa figura. Assim, se dividirmos o cone em duas partes, temos uma que contém o vértice, e outra, que contém a base.

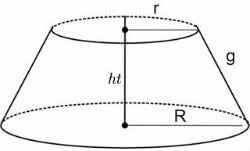
Essa última é chamada de “tronco do cone”. Em relação a área é possível calcular:

Fórmula da área da base menor (A_b)

A_b = π.r²

Fórmula da área da base maior (A_B)

A_B = π.R²

Fórmula da área lateral (A_l)

A_l = π.g. (R + r)

Fórmula da área total (A_t)

A_t = A_B + A_b + A_l

Exemplos 1
Qual a área lateral e a área total de um cone circular reto que possui altura de 8 cm e o raio da base de 6 cm?

Resolução

Primeiramente, temos que calcular a geratriz desse cone:

g = √r² + h²
g = √6² + 8²
g = √36 + 64
g = √100
g = 10 cm

Feito isso, podemos calcular a área lateral através da fórmula:

A_l= π.r.g
A_l= π.6.10
A_l= 60π cm²

Pela fórmula da área total, temos:

A_t = π.r (g+r)
At = π.6 (10+6)
At = 6π (16)
At = 96π cm²

Poderíamos resolver de outra maneira, ou seja, somando as áreas da lateral e da base:

A_t= 60π + π.6²
A_t = 96π cm²

Exemplo 2
Encontre a área total do tronco do cone que apresenta altura de 4 cm, a base maior um círculo de diâmetro de 12 cm e a base menor um círculo de diâmetro de 8 cm.

Resolução

Para encontrar a área total desse tronco de cone, é necessário encontrar as áreas da base maior, menor e ainda, da lateral.

Além disso, é importante lembrar o conceito de diâmetro, que equivale duas vezes a medida do raio (d = 2r). Assim, pelas fórmulas temos:

Área da Base Menor

A_b = π.r²
A_b = π.4²
A_b = 16π cm²

Área da Base Maior

A_B = π.R²
A_B = π.6²
A_B = 36π cm²

Área Lateral

Antes de encontrar a área lateral, temos que encontrar a medida da geratriz da figura:

g² = (R – r)²+ h²
g² = (6 – 4)² + 4²
g² = 20
g = √20
g = 2√5

Feito isso, vamos substituir os valores na fórmula da área lateral:

A_l = π.g. (R + r)
A_l = π . 2√5 . (6 + 4)
A_l = 20π√5 cm²

Área Total

A_t = A_B + A_b + A_l
A_t = 36π + 16π + 20π√5
A_t = (52 + 20√5)π cm²

Exercícios de área do cone

Exercício 1

(UECE) Um cone circular reto, cuja medida da altura é h, é secionado, por um plano paralelo à base, em duas partes: um cone cuja medida da altura é h/5 e um tronco de cone, conforme a figura:

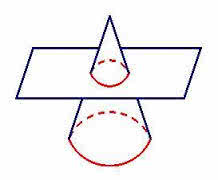
A razão entre as medidas dos volumes do cone maior e do cone menor é:

a) 15
b) 45
c) 90
d) 125

Ver Resposta

Resposta: d) 125

Volume do cone maior

$reto V com maior subscrito igual a numerador Ab com maior subscrito. reto h sobre denominador 3 fim da fração$

Volume do cone menor

$reto V com menor subscrito igual a numerador Ab com menor subscrito. começar estilo mostrar reto h sobre 5 fim do estilo sobre denominador 3 fim da fração igual a Ab com menor subscrito. reto h sobre 5 espaço. espaço 1 terço igual a numerador Ab com menor subscrito. reto h sobre denominador 15 fim da fração$

Para encontrar uma relação entre as bases, vamos compará-las aos quadrados das alturas.

$Ab com maior subscrito sobre Ab com menor subscrito igual a abre parênteses reto h com maior subscrito sobre reto h com menor subscrito fecha parênteses ao quadrado Ab com maior subscrito sobre Ab com menor subscrito igual a reto h com maior subscrito ao quadrado sobre reto h com menor subscrito ao quadrado Ab com maior subscrito igual a numerador reto h com maior subscrito ao quadrado. espaço Ab com menor subscrito sobre denominador reto h com menor subscrito ao quadrado fim da fração$

Temos também que a altura menor é hmaior/5.

$Ab com maior subscrito igual a numerador reto h com maior subscrito ao quadrado. espaço Ab com menor subscrito sobre denominador abre parênteses começar estilo mostrar reto h com m a i o r subscrito fim do subscrito sobre 5 fim do estilo fecha parênteses ao quadrado fim da fração Ab com maior subscrito igual a numerador reto h com maior subscrito ao quadrado. espaço Ab com menor subscrito sobre denominador começar estilo mostrar reto h com m a i o r subscrito fim do subscrito ao quadrado sobre 5 ao quadrado fim do estilo fim da fração Ab com maior subscrito igual a numerador reto h com maior subscrito ao quadrado. espaço Ab com menor subscrito sobre denominador começar estilo mostrar reto h com m a i o r subscrito fim do subscrito ao quadrado sobre 25 fim do estilo fim da fração Ab com maior subscrito igual a reto h com maior subscrito ao quadrado. espaço Ab com menor subscrito espaço. espaço 25 sobre reto h com m a i o r subscrito fim do subscrito ao quadrado Ab com maior subscrito igual a riscado diagonal para cima sobre reto h com maior subscrito ao quadrado fim do riscado. espaço Ab com menor subscrito espaço. espaço numerador 25 sobre denominador riscado diagonal para cima sobre reto h com m a i o r subscrito fim do subscrito ao quadrado fim do riscado fim da fração Ab com maior subscrito igual a 25 espaço. espaço Ab com menor subscrito espaço$

Escrevendo a razão entre os volumes:

$reto V com maior subscrito sobre reto V com menor subscrito igual a numerador numerador Ab com maior subscrito. reto h sobre denominador 3 fim da fração sobre denominador numerador Ab com menor subscrito. reto h sobre denominador 15 fim da fração fim da fração reto V com maior subscrito sobre reto V com menor subscrito igual a numerador Ab com maior subscrito. reto h sobre denominador 3 fim da fração. numerador 15 sobre denominador Ab com menor subscrito. reto h fim da fração reto V com maior subscrito sobre reto V com menor subscrito igual a numerador Ab com maior subscrito. diagonal para cima risco reto h sobre denominador 1 fim da fração. numerador 5 sobre denominador Ab com menor subscrito. diagonal para cima risco reto h fim da fração reto V com maior subscrito sobre reto V com menor subscrito igual a numerador 5. Ab com maior subscrito sobre denominador Ab com menor subscrito fim da fração$

Substituindo a relação da área maior:

$reto V com maior subscrito sobre reto V com menor subscrito igual a numerador 5.25. Ab com menor subscrito sobre denominador Ab com menor subscrito fim da fração reto V com maior subscrito sobre reto V com menor subscrito igual a numerador 125. riscado diagonal para cima sobre Ab com menor subscrito fim do riscado sobre denominador riscado diagonal para cima sobre Ab com menor subscrito fim do riscado fim da fração reto V com maior subscrito sobre reto V com menor subscrito igual a 125$

Exercício 2

(Mackenzie-SP) Um frasco de perfume, que tem a forma de um tronco de cone circular reto de raios 1 cm e 3 cm, está totalmente cheio. Seu conteúdo é despejado em um recipiente que tem a forma de um cilindro circular reto de raio 4 cm, como mostra a figura.

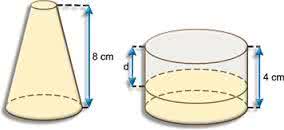
Se d é a altura da parte não preenchida do recipiente cilíndrico e, adotando-se π = 3, o valor de d é:

a) 10/6
b) 11/6
c) 12/6
d) 13/6
e) 14/6

Ver Resposta

Alternativa b: 11/6

Passo 1: igualdade entre o volume do tronco e da parte cheia do cilindro.

$reto V com tronco subscrito igual a reto V com cheio espaço do espaço cilindro subscrito fim do subscrito$

Passo 2: cálculo do volume do tronco.

$reto V com tronco subscrito igual a reto V com total espaço subscrito fim do subscrito menos reto V com volume espaço do espaço cone espaço menor subscrito fim do subscrito$

Para determinar os volumes do cone total e da parte menor, é preciso determinar a altura do cone total. Para isso, utilizamos a semelhança de triângulos.

$reto H sobre 3 igual a reto h sobre 1$

Onde H é a altura total do cone e h é a altura do cone menor (da ponta do cone).

Fazendo meio pelas extremos:

$reto H espaço. espaço 1 espaço igual a espaço 3 espaço. espaço reto h reto H igual a 3 reto h$

Volume do cone total

$reto V com total subscrito igual a numerador reto pi.3 ao quadrado.3 reto h sobre denominador 3 fim da fração igual a numerador 27 reto pi reto h sobre denominador 3 fim da fração$

Volume do cone menor

$reto V com cone espaço menor subscrito fim do subscrito igual a numerador reto pi.1 ao quadrado. reto h sobre denominador 3 fim da fração igual a numerador reto pi reto h sobre denominador 3 fim da fração$

Substituindo na fórmula do tronco:

$reto V com tronco subscrito igual a numerador 27 reto pi reto h sobre denominador 3 fim da fração menos numerador reto pi reto h sobre denominador 3 fim da fração igual a numerador 26 reto pi reto h sobre denominador 3 fim da fração$

Como

$reto H igual a 3 reto h 8 mais reto h igual a 3 reto h 8 igual a 3 reto h menos reto h 8 igual a 2 reto h reto h igual a 8 sobre 2 igual a 4$

$reto V com tronco subscrito igual a numerador 26 reto pi.4 sobre denominador 3 fim da fração igual a numerador 104 reto pi sobre denominador 3 fim da fração$

Passo 3: cálculo do volume do cilindro (parte cheia).

A altura de líquido dentro do cilindro é a altura total (4 cm) menos d.

$reto V com cilindro subscrito igual a reto pi.4 ao quadrado. parêntese esquerdo 4 menos reto d parêntese direito reto V com cilindro subscrito igual a reto pi.16. parêntese esquerdo 4 menos reto d parêntese direito reto V com cilindro subscrito igual a reto pi parêntese esquerdo 64 menos 16 reto d parêntese direito$

Passo 4: substituir os volumes do cilindro e do cone na relação do passo 1, e resolver para d.

$reto V com tronco subscrito igual a reto V com cheio espaço do espaço cilindro subscrito fim do subscrito numerador 104 reto pi sobre denominador 3 fim da fração igual a reto pi parêntese esquerdo 64 menos 16 reto d parêntese direito$

Podemos cancelar o valor de $reto pi$ .

$numerador 104 diagonal para cima risco reto pi sobre denominador 3 fim da fração igual a diagonal para cima risco reto pi parêntese esquerdo 64 menos 16 reto d parêntese direito 104 sobre 3 igual a 64 menos 16 reto d 16 reto d espaço igual a espaço 64 espaço menos espaço 104 sobre 3 16 reto d espaço igual a espaço numerador 3.64 sobre denominador 3 fim da fração menos espaço 104 sobre 3 16 reto d espaço igual a espaço numerador 192 menos 104 sobre denominador 3 fim da fração 16 reto d espaço igual a 88 sobre 3 reto d igual a numerador 88 sobre denominador 3.16 fim da fração reto d igual a 88 sobre 48$

Simplificando

$reto d igual a 88 sobre 48 igual a 44 sobre 24 igual a 22 sobre 12 igual a 11 sobre 6$

Exercício 3

(UFRN) Um abajur em formato de cone equilátero está sobre uma escrivaninha, de modo que, quando aceso, projeta sobre esta um círculo de luz (veja a figura abaixo).

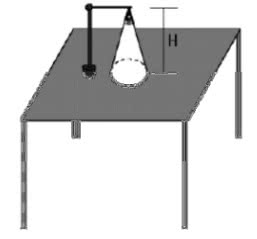
Se a altura do abajur, em relação à mesa, for H = 27 cm, a área do círculo iluminado, em cm² será igual a:

a) 225π
b) 243π
c) 250π
d) 270π

Ver Resposta

Alternativa b: 243π

Em um cone equilátero a geratriz é igual ao diâmetro, ou seja, duas vezes o raio. Assim, a o raio é a metade da geratriz.

$reto g igual a 2 reto R reto R igual a reto g sobre 2$

Formamos um triângulo retângulo entre a altura, o raio da base e a geratriz, sendo esta a hipotenusa.

Pelo Teorema de Pitágoras:

$reto g ao quadrado igual a reto R ao quadrado mais reto H ao quadrado reto g ao quadrado igual a g ao quadrado sobre 4 mais H ao quadrado reto g ao quadrado menos reto g ao quadrado sobre 4 igual a reto H ao quadrado numerador 4. reto g ao quadrado sobre denominador 4 fim da fração menos reto g ao quadrado sobre 4 igual a reto H ao quadrado numerador 3 reto g ao quadrado sobre denominador 4 fim da fração igual a reto H ao quadrado$

Substituindo o valor de H e resolvendo para g:

$numerador 3 reto g ao quadrado sobre denominador 4 fim da fração igual a 27 ao quadrado 3 reto g ao quadrado igual a 729.4 3 reto g ao quadrado igual a 2 espaço 916 reto g ao quadrado igual a numerador 2 espaço 916 sobre denominador 3 fim da fração reto g ao quadrado igual a 972 reto g igual a raiz quadrada de 972$

Determinando o valor de R.

$reto R igual a reto g sobre 2$

Elevando os dois termos ao quadrado:

$reto R ao quadrado igual a reto g ao quadrado sobre 4$

Temos que g ao quadrado é igual a 972.

$reto R ao quadrado igual a 972 sobre 4 igual a 243$

Cálculo da área da base.

$reto A com reto b subscrito igual a reto pi. reto R ao quadrado reto A com reto b subscrito igual a 243 reto pi$

Cálculo da Área do Cone: fórmulas e exercícios

Fórmula da área da base

Fórmula da área Lateral

Fórmula da área total

Área do Tronco do Cone

Fórmula da área da base menor (Ab)

Fórmula da área da base maior (AB)

Fórmula da área lateral (Al)

Fórmula da área total (At)

Exercícios de área do cone

Exercício 1

Exercício 2

Exercício 3

Fórmula da área da base menor (A_b)

Fórmula da área da base maior (A_B)

Fórmula da área lateral (A_l)

Fórmula da área total (A_t)